Расчет транзисторного автогенератора с кварцевым резонатором
 Скачать 491.21 Kb. Скачать 491.21 Kb.
|
|
1.3.4. Расчет автогенератора с кварцевым резонатором в цепи обратной связи При разработке методики расчета АГ (см. рис.1.5), как и в предыдущем случае, воспользуемся уравнением стационарного состояния: 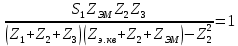 , (1.16) , (1.16)где Z1+Z2+Z3=Rк+jωгLк+1/(jωгCк)≈Rк(1+jαк); αк=2Qк(fг−fк)/fк – обобщенная расстройка; Qк – нагруженная добротность контура в коллекторной цепи АГ; 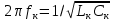 ; Cк=C1C2/(C1+C2) – емкость контура; Rк – собственное сопротивление потерь в контуре; Zэм=Rэм+jXэм – комплексное сопротивление, представляющее собой параллельное соединение входного сопротивления транзистора, включенного по схеме с общей базой, и резистора в эмиттерной цепи R4. ; Cк=C1C2/(C1+C2) – емкость контура; Rк – собственное сопротивление потерь в контуре; Zэм=Rэм+jXэм – комплексное сопротивление, представляющее собой параллельное соединение входного сопротивления транзистора, включенного по схеме с общей базой, и резистора в эмиттерной цепи R4.Учитывая, что наибольшую стабильность частоты АГ можно получить только при совпадении частоты генерации с частотой последовательного резонанса КвР, в дальнейшем будем считать fг=fкв. Фазовый угол средней крутизны транзистора при его включении по схеме с общей базой существенно меньше, чем в схеме с общим эмиттером, что позволяет считать крутизну транзистора вещественной и положить S1=S1.0. Кроме того учтем, что емкость кварцедержателя C0 нейтрализована индуктивностью L0, выбранной из условия 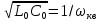 . Тогда, записав соотношение (1.16) отдельно для мнимых и вещественных составляющих и выполнив необходимые преобразования, получим уравнения баланса фаз и баланса амплитуд: . Тогда, записав соотношение (1.16) отдельно для мнимых и вещественных составляющих и выполнив необходимые преобразования, получим уравнения баланса фаз и баланса амплитуд:αк = tgs≈ 0, т. е. ωг = ωкв; (1.17) 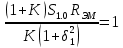 , (1.18) , (1.18)где 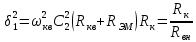 ; RЭМ=R4/(1+S1.0R4); K=C1/C2; Rвн – сопротивление, вносимое в контур цепью обратной связи; Rк – сопротивление потерь в контуре. ; RЭМ=R4/(1+S1.0R4); K=C1/C2; Rвн – сопротивление, вносимое в контур цепью обратной связи; Rк – сопротивление потерь в контуре.В процессе расчета необходимо определить параметры колебательной системы АГ (Lк и Cк) и цепи обратной связи (K и R4). Поэтому, помимо уже имеющихся двух уравнений (1.17) и (1.18), необходимо составить еще два. Одним из них может служить уравнение, связывающее мощность, рассеиваемую КвР, с параметрами АГ, т.е. 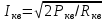 . Учтя, что Iкв=Uб/Rэм=Uб(1+S1.0)/R4, можно получить . Учтя, что Iкв=Uб/Rэм=Uб(1+S1.0)/R4, можно получить 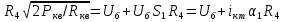 . Из последнего соотношения следует, что . Из последнего соотношения следует, что 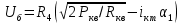 . Нетрудно заметить, что полученное равенство выполняется лишь при условии . Нетрудно заметить, что полученное равенство выполняется лишь при условии 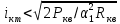 , которое необходимо учесть при выборе амплитуды импульса коллекторного тока транзистора. , которое необходимо учесть при выборе амплитуды импульса коллекторного тока транзистора.Таким образом, задавшись значениями iкm, θ и Pкв, по известным параметрам КвР и транзистора можно рассчитать R4 и определить Rэм. Поскольку эквивалентное сопротивление контура без учета потерь, вносимых цепью Rкв, Rэм, определяется равенством 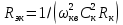 , где Cк=C2K/(1+ K), приведем выражение для , где Cк=C2K/(1+ K), приведем выражение для 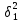 к виду: к виду: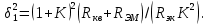 С учетом последнего равенства уравнение баланса амплитуд может быть представлено как: 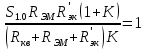 , (1.19) , (1.19)где 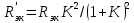 – эквивалентное сопротивление контура в точках подключения кварцевого резонатора. – эквивалентное сопротивление контура в точках подключения кварцевого резонатора.Высокая фиксирующая способность КвР может быть реализована только в том случае, если выполнено условие Rкв>R′эк. Практически достаточно, чтобы Rкв=(3...5)R′эк. С учетом изложенного, из соотношения (1.19) можно определить значения коэффициента K и Rэк. Затем, задавшись реализуемой добротностью контура Qк=1/(ωквCкRк)=50...100, определяют волновое сопротивление контура ρк=1/(ωквCк)=ωквLк=Rэк/Qк и значения Cк и Lк. Порядок расчета АГ изложен в приводимом далее примере. Пример расчета Рассчитать параметры и режим работы АГ, работающего на частоте 15МГц и выполненного на транзисторе ГТ313. Параметры транзистора: fт=900МГц, β0=50, Sгр=0,05А/В, Eб0=0,25В, rб=60Ом, iк.доп=0,03A, Pк.доп=0,5мВт. Параметры кварцевого резонатора: fкв=15МГц, Rкв=11Ом, C0=7пФ, Qкв=67000. Задаемся мощностью, рассеиваемой КвР, Pкв=0,2 мВт. Расчет параметров транзистора 1. Максимально возможная амплитуда импульса коллекторного тока транзистора: 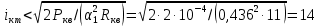 мA. мA.2. Задаемся iкm=5мА и определяем S0=0,081A/B, S1.0=0,023A/B, Uб=0,11В. Расчет параметров колебательной системы и цепи обратной связи 1. Сопротивление резистора в эмиттерной цепи: 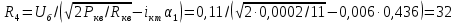 Ом. Ом.2. Сопротивление Rэм=R4/(1+S1.0R4)=32/(1+0,023⋅32)=18,4Ом. Задаемся R′эк=0,25Rкв=0,25⋅11=2,75Ом. 3. Вспомогательный параметр: A= S1.0RэмRэк/(Rкв+Rэм+Rэк)=0,02318,4 2,75/(11+18,4+2,75)=0,036. 4. Отношение емкостей K=A/(1−A)=0,036/(1−0,036)=0,037. 5. Эквивалентное сопротивление контура: Rэк=R′эк(1+ K)2/K2=2,75(1+0,037)2/0,0372=2160Ом. 6. Задаемся добротностью контура Qк=50. 7. Параметры колебательной системы: ρк=Rэк/Qк=2160/50=43,2Ом; Cк=1/(2πfквρк)=1/(2π15106 43,2)=246пФ; Lк=ρк/(2πfкв)=43,2/(2π15106)=0,458мкГн; C2=Cк(1+K)/K=246(1+0,037)/0,037=6894пФ; С1=KС2=0,0376894=255пФ. 8. Индуктивность, нейтрализующая емкость кварцедержателя: L0=1/((2fкв)2C0)=1/(42(15106)2710-12)=16,1мкГн. Расчет энергетических параметров автогенератора 1. Параметр 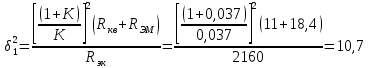 . .2. Сопротивление коллекторной нагрузки транзистора: Rк.н=Rэк/((1+K)2(1+1/12))=2160/(1+0,037)2(1+1/10,7))=1837Ом. 3. Амплитуда напряжения на коллекторе: Uк=iкm1Rк.н=510-30,4361837=4,005В. Далее из условия получения недонапряженного режима работы выбирается Eк, рассчитываются потребляемая мощность, мощность, отдаваемая транзистором, мощность, рассеиваемая на коллекторе, и КПД коллекторной цепи. При расчете цепей питания необходимо учесть, что база транзистора заземлена по высокой частоте. Поэтому при расчете делителя R1, R2 необходимо задаться током через делитель Iд=(5...10)Iб0, а затем воспользоваться приведенными ранее соотношениями. 1.3.5. Расчет автогенератора с кварцевым резонатором в контуре Уравнение стационарного режима для АГ (см. рис. 1.6) имеет вид: 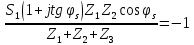 , (1.20) , (1.20)где Z1=−jX1=1/(jωгC1); Z2=−jX2=1/(jωгC2); Z3=jωгLк+Z′э.кв; Z′э.кв=R′э.кв+jX′э.кв=Rкв(1− δ)[1+ j(α−δ)] – эквивалентное сопротивление КвР с учетом шунтирующего действия R0 (см.1.3.1); δ=ωквC0Rкв; α=2Qкв(fг−fкв)/fкв. Поскольку Rкв существенно больше собственного сопротивления потерь в контуре, последнее в расчетах не учитывается. Крутизна фазочастотной характеристики резонатора, зашунтированного резистором R0, равна 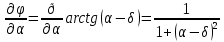 и достигает максимального значения при α=δ. Следовательно, для обеспечения максимальной стабильности частоты частота генерируемых колебаний должна быть практически равна частоте последовательного резонанса КвР. Заменив в условии стационарности (1.20) ωг на ωкв и выделив отдельно мнимую и вещественную части равенства, нетрудно получить: и достигает максимального значения при α=δ. Следовательно, для обеспечения максимальной стабильности частоты частота генерируемых колебаний должна быть практически равна частоте последовательного резонанса КвР. Заменив в условии стационарности (1.20) ωг на ωкв и выделив отдельно мнимую и вещественную части равенства, нетрудно получить:Xк =R′э.квtgs; (1.21) X1X2S1coss/R′э.кв=1, (1.22) где Xк – реактивное сопротивление по обходу колебательной системы на частоте генерации. При расчете колебательной системы АГ необходимо определить Lк, C1 и C2. Поэтому помимо двух уравнений (1.21) и (1.22) необходимо составить еще одно. Таким уравнением может быть уравнение, связывающее мощность, рассеиваемую КвР, с напряжением на базе транзистора, током через резонатор и параметрами колебательной системы, т.е. 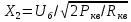 . .Таким образом, выбрав транзистор и кварцевый резонатор и задавшись iкm, θ и Pкв можно определить Xк, X1X2 и X3, т.е. рассчитать колебательную систему автогенератора. Пример расчета Рассчитать параметры и режим работы АГ, работающего на частоте 10МГц и выполненного на транзисторе ГТ313. Необходимые для расчета параметры транзистора: iкm=6мA; S0=0,081A/B; s=−3,5°; Iк1=2,62мA. Параметры кварцевого резонатора: fкв=10МГц; C0=5пФ; Pкв=0,3мВт; Qкв=34000; Rкв=35Ом. Задаемся Pкв=0,3мВт. Расчет параметров колебательной системы 1. Вспомогательный параметр δ=2πfквC0Rкв=2π107510−1235=0,011. 2. Резистивное сопротивление КвР R′э.кв=Rкв (1−δ)≈Rкв=35Ом. 3. Реактивное сопротивление по обходу колебательной системы: Xк=R′э.квtgs=−350,061=−2,14Ом. 4. Произведение X1X2=R’кв/(S1.0cos2s)= 35/(0,0230,996)=1522Ом2. 5. Амплитуда напряжения на базе транзистора: Uб=Iк1/S1=2,6210-3/2310-3=0,11В. 6. Cопротивление шунтирующего резонатор резистора: R0=1/(2fквC0)=1/(2107510-12)=3184Ом. 7. Амплитуда первой гармоники тока через резонатор: 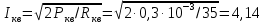 мА. мА.8. Сопротивления конденсаторов колебательной системы: X2=Uб/Iкв=0,11/4,1410-3=26,6Ом; X1=X1X2/X2=1522/26,6=57,2Ом. 9. Емкости конденсаторов: C1=1/(2πfквX1)=1/(2π10757,2)=278пФ; C2=1/(2πfквX2)=1/(2π10726,6)=608пФ. 10. Сопротивление индуктивности контура: XL=Xк+X1+X2=−21,4+57,2+26,6=81,66 Ом. 11. Индуктивность контура: Lк=XL/(2πfкв)=81,66/(2π107)=1,3мкГн. 12. Эквивалентное сопротивление контура: Rэк=X12/Rкв=57,22/35=93,6Ом. Далее следует расчет энергетических характеристик АГ и элементов цепей питания, который может быть выполнен на основании приведенных ранее соотношений. Однако при выборе блокировочных и разделительных элементов необходимо учитывать специфические особенности рассчитываемой схемы. |
