Курсовая. Исправленная курсовая. Расчетная схема Дано
 Скачать 0.75 Mb. Скачать 0.75 Mb.
|
 Расчетная схема: 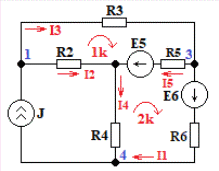 Дано: E5 = 40 В; E6 = 20 В J = 0,6 A R2 = 1 Ом; R3 = 8 Ом R4 = 7 Ом; R5 = 4 Ом; R6 = 6 Ом Найти: В соответствии с заданием. 1. Кирхгоф. Уравнения. Согласно 1-му закону Кирхгофа для узлов: уз.1: -I2 - I3 = -J уз.2: I2 - I4 + I5 = 0 (1) уз.3: -I1 + I3 - I5 = 0 Согласно 2-му закону Кирхгофа для контуров: Обход контуров по часовой стрелке. конт.1: -R2*I2 + R3*I3 + R5*I5 = E5 конт.2: R6*I1 - R4*I4 - R5*I5 = -Е5 + E6 (2) Подставим значения в (1) и (2): -I2 - I3 = -0,6 I2 - I4 + I5 = 0 -I1 + I3 - I5 = 0 -1*I2 + 8*I3 + 4*I5 = 40 6*I1 - 7*I4 - 4*I5 = -20 Система из 5-ти уравнений готова для решения. Систему решаем матричным методом. Числа перед неизвестными токами образуют матрицу коэффициентов (квадратная, 5х5), сами неизвестные образуют матрицу столбец переменных (1х5), а правые части системы - матрицу-столбец свободных членов (1х5). Решаем с привлечением программного обеспечения. Решаем методом Крамера. (используем ПО ресурса - http://matrix.reshish.ru/cramer.php) Матрица коэффициентов |A|: 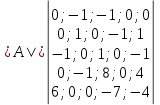 Вектор свободных членов |B|: 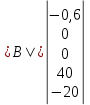 Определитель основной матрицы системы: Δ = -205 Определители переменных: (которые являются определителями матриц, полученных из матрицы А заменой k - ого столбца (k = 1, 2, …, n) на столбец свободных членов) 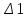 = 43 = 43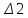 = 504 = 504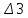 = -627 = -627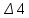 = -166 = -166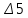 = -670 = -670Решение системы (|A|*||= |B|) Токи ветвей: I1 = Δ1/Δ = -0,2098 A I2 = Δ2/Δ = -2,4585 A I3 = Δ3/Δ = 3,0585 A I4 = Δ4/Δ = 0,8098 A I5 = Δ5/Δ = 3,2683 A Знак минус говорит о том, что фактическое направление тока противоположно. 2. Метод контурных токов. Предполагается, что в каждом независимом контуре течет свой неизменный контурный ток. Уравнения составляют относительно контурных токов, после чего определяют токи ветвей через контурные токи. При расчете МКТ полагают, что в каждом независимом контуре протекает неизменный (виртуальный) контурный ток. Если какая-либо ветвь относится лишь к одному конкретному контуру, то значение протекающего в нем реального тока будет равно контурному. В том случае, когда ветвь входит в состав сразу нескольких контуров, ток, протекающий в ней, будет представлять собой сумму, включающую в себя соответствующие контурные токи. В этом случае обязательно учитывается направление (знак) обхода контуров. Обход контуров выберем по часовой стрелке. Расчетная схема. 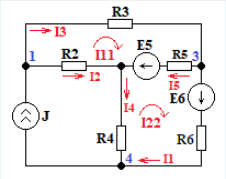 Дано: E5 = 40 В; E6 = 20 В J = 0,6 A R2 = 1 Ом; R3 = 8 Ом R4 = 7 Ом; R5 = 4 Ом; R6 = 6 Ом 2. 1. Контурные уравнения: (R2 + R3 + R5)*I11 - R5*I22 = E5 + R2*J -R5*I11 + (R4 + R5 + R6)*I22 = E6 - E5 + R4*J Подставим значения: 13*I11 - 4*I22 = 40,6 -4*I11 + 17*I22 = -15,8 Решаем методом Крамера. Матрица коэффициентов |A|: 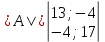 Вектор свободных членов |B|: 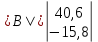 Определитель основной матрицы системы: Δ = 205 Определители переменных: 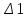 = 627 = 627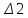 = -43 = -43Решение системы (|A|*|Iii|= |B|) Контурные токи: I11 = Δ1/Δ = 3,0585 A I  22 = Δ2/Δ = -0,2098 A 22 = Δ2/Δ = -0,2098 A2. 2. Токиветвей. I1 = I22 = -0,2098 A I2 = -I11 + J = -3,0585 + 0,6 = -2,4585 A I3 = I11 = 3,0585 A I4 = -I22 + J = 0,2098 + 0,6 = 0,8098 A I5 = I11 - I22 = 3,0585 + 0,2098 = 3,2683 A Знак минус говорит о том, что фактическое направление тока противоположно. 3. Баланс мощностей. Мощность, потребляемая нагрузкой, должна совпадать с мощностью, генерируемой источниками - закон сохранения энергии. Исходные данные: E5 = 40 В; E6 = 20 В J = 0,6 A R2 = 1 Ом; R3 = 8 Ом R4 = 7 Ом; R5 = 4 Ом; R6 = 6 Ом I1 = -0,2098 A; I2 = -2,4585 A I3 = 3,0585 A; I4 = 0,8098 A I5 = 3,2683 A 3. 1. Нагрузка: Мощность, выделяемую в нагрузке определяем как: Pнагр = ΣPi = ΣRi*Ii2, Вт Pнагр = R6*I12 + R2*I22 + R3*I32 + R4*I42 + R5*I52 = = 6*0,044 + 1*6,044 + 8*9,354 + 7*0,656 + 4*10,682 = 128,46 Вт 3. 2. Источник: Мощность, генерируемая источниками ЭДС: Pист = ΣPej = ΣEj*Ij, Вт Pист = E5*I2 + E6*I3 + Uj*J = = 40*3,2683 + 20*(-0,2098) + 3,2101*0,6 = 128,46 Вт Напряжение на источнике тока: Uj = R2*I2 + R4*I4 = -1*2,4585 + 7*0,8098 = 3,2101 В Баланс сошелся. Задача решена верно. Отметим, что источник Е6 работает в режиме нагрузки (как если бы заряжался аккумулятор).  Расчетная схема: 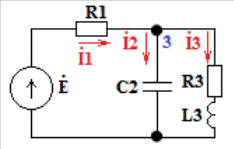 Дано: e(t) = 60,5*sin(100*t - 15) В R1 = 6 Ом; C2 = 1000 мкФ R3 = 6 Ом; L3 = 90 мГн Найти: В соответствии с заданием. 1. Параметры элементов цепи: ω = 2*f *π = 100 рад/с Источник: Расчет ведем в комплексах действующих значений. 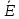 = E = E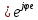 = 42,78 = 42,78 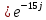 = 41,32 - 11,07j В = 41,32 - 11,07j ВE = Em/ 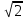 = 26/ = 26/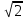 = 42,78 В = 42,78 Вφe = 0 град. Комплексные сопротивления ветвей: z1 = R1 = 6 = 6* 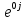 , Ом , Омz2 = jxL = -10j = 10* 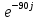 , Ом , Омxc2 = 1/(ω*C2) = 1000000/(100*1000) = 10 Ом z3 = R3 + jxL3 = 6 + 9j = 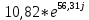 , Ом , ОмxL = ω*L3 = 100*0,09 = 9 Ом Эквивалентное комплексное сопротивление параллельных ветвей: zp = 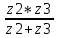 = = 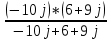 = 16,22 - 7,3j = 17,79* = 16,22 - 7,3j = 17,79*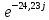 , Ом , ОмЭквивалентное комплексное сопротивление цепи: zэ = z1 + zp = = 6 + 16,22 - 7,3j = 22,22 - 7,3j = 23,39* 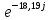 , Ом , Ом2. Токи ветвей: Расчет ведем в комплексах действующих значений. Ток в неразветвленной части (источника): 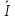 1 = 1 = 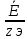 = = 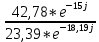 = 1,83* = 1,83*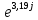 = 1,83 + 0,1j A = 1,83 + 0,1j AНапряжение на параллельных ветвях: 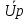 = zp* = zp*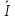 1 = 1 == 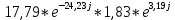 = 32,56* = 32,56*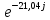 = 30,39 - 11,69j В = 30,39 - 11,69j ВТоки параллельных ветвей: 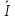 2 = 2 = 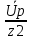 = = 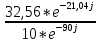 = 3,26* = 3,26*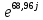 = 1,17 + 3,04j A = 1,17 + 3,04j A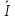 3 = 3 = 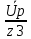 = = 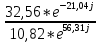 = 3,01* = 3,01*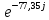 = 0,66 - 2,94j A = 0,66 - 2,94j AМгновенные токи: 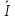 1 = 1,83* 1 = 1,83*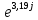 A Ai1(t) = Im1*sin(ω*t + φi1) = 2,59*sin(100*t + 3,19) A Im1 = I1* 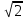 = 1,83* = 1,83*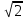 = 2,59 A = 2,59 Aφi1 = 3,19 град. 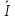 2 = 3,26* 2 = 3,26*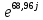 A Ai2(t) = Im2*sin(ω*t + φi2) = 4,61*sin(100*t + 68,96) A Im2 = I2* 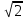 = 3,26* = 3,26*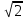 = 4,61 A = 4,61 Aφi2 = 68,96 град. 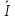 3 = 3,01* 3 = 3,01*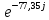 A Ai3(t) = Im3*sin(ω*t + φi3) = 4,26*sin(100*t - 77,35) A Im3 = I3* 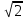 = 3,01* = 3,01*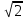 = 4,26 A = 4,26 Aφi3 = -77,35 град. 3. Напряжения на элементах ветвей: 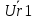 = (6)*(1,83 + 0,1j) = 10,98 + 0,6j = 11* = (6)*(1,83 + 0,1j) = 10,98 + 0,6j = 11*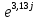 В В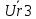 = R3* = R3*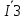 = (6)*(0,66 - 2,94j) = 3,96 - 17,64j = 18,08* = (6)*(0,66 - 2,94j) = 3,96 - 17,64j = 18,08*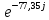 В В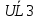 = jxL3* = jxL3*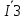 = (9j)*(0,66 - 2,94j) = 26,46 + 5,94j = 27,12* = (9j)*(0,66 - 2,94j) = 26,46 + 5,94j = 27,12*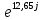 В В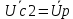 = 32,56* = 32,56*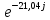 = 30,39 - 11,69j В = 30,39 - 11,69j ВМгновенные напряжения : 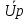 = 32,56* = 32,56*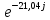 В Вup(t) = Ump*sin(ω*t + φup) = 46,05*sin(100*t - 21,04) В Ump = Up* 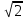 = 32,56* = 32,56*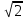 = 46,05 В = 46,05 Вφup = -21,04 град. 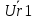 = 11* = 11*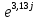 В Вur1(t) = Umr1*sin(ω*t + φur1) = 15,56*sin(100*t + 3,13) В Umr1 = Ur1* 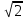 = 11* = 11*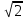 = 15,56 В = 15,56 Вφur1 = 3,13 град. 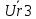 = 18,08* = 18,08*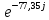 В Вur3(t) = Umr3*sin(ω*t + φur3) = 25,57*sin(100*t - 77,35) В Umr3 = Ur3* 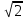 = 18,08* = 18,08*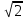 = 25,57 В = 25,57 Вφur3 = -77,35 град. 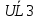 = 27,12* = 27,12*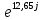 В ВuL3(t) = UmL3*sin(ω*t + φuL3) = 38,35*sin(100*t + 12,65) В UmL3 = UL3* 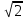 = 27,12* = 27,12*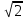 = 38,35 В = 38,35 ВφuL3 = 12,65 град. 4. Мощность. 4. 1. Мощность ветвей: Расчет ведем по выражению: 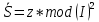 , где mod(I) - модуль комплекса тока , где mod(I) - модуль комплекса тока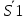 =z1 =z1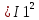 = (6)*3,36 = 20,16 ВА = (6)*3,36 = 20,16 ВАP1 = 20,16 Вт Q1 = 0 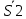 = z2 = z2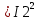 = (-10j)*10,61 = -106,1j ВА = (-10j)*10,61 = -106,1j ВАP2 = 0 Q2 = -106,1 вар (емкостн.) 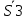 = z3 = z3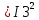 = (6 + 9j)*9,08 = 54,48 + 81,72j ВА = (6 + 9j)*9,08 = 54,48 + 81,72j ВАP3 = 54,48 Вт Q3 = 81,72 вар (индуктивн.) 4. 2. Итого по нагрузке: 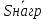 = = 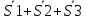 = 20,16 - 106,1j + 54,48 + 81,72j = = 20,16 - 106,1j + 54,48 + 81,72j = = 74,64 - 24,38j ВА Pнагр = 74,64 Вт Qнагр = -24,38 вар (емкостн.) 4. 3. Мощность источника: Расчет ведем по выражению: 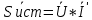 , где , где 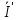 - комплексно-сопряженный ток. - комплексно-сопряженный ток.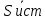 = (41,32 - 11,07j)*(1,83 - 0,1j) = 74,51 - 24,39j ВА = (41,32 - 11,07j)*(1,83 - 0,1j) = 74,51 - 24,39j ВАPист = 74,51 Вт Qист = -24,39 вар (емкостн.) 4. 4. Погрешность расчета: dP = 100*|(Pнагр - Pист)|/Pист = 100*|(74,64 - 74,51)|/74,51 = 0,174 % dQ = 100*|(Qнагр - Qист)|/Qист = 100*|(24,38 - 24,39)|/24,39 = 0,041 % Не существенное расхождение объясняется округлением. Баланс сошелся, задача решена верно. 5. Векторная диаграмма: Используем ранее рассчитанные значения Ui. Масштаб по току mI: 1 дел. - 1 А 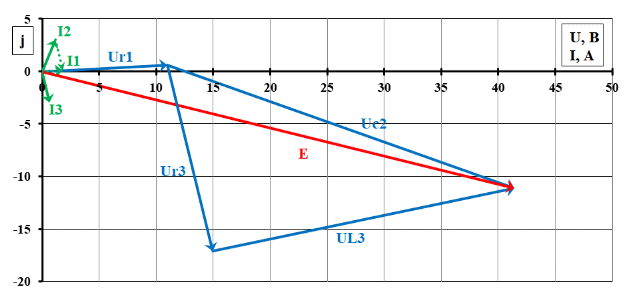  Расчетная схема: 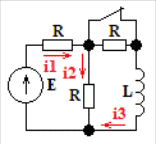 Дано: E = 210 R = 80 Ом; L = 600 мГн Найти: В соответствии с заданием. Классический метод. 1. Токи и напряжения в моменты t(0-), t(0+) и t(∞) В установившемся режиме на постоянном токе индуктивность - закоротка. t(0-) 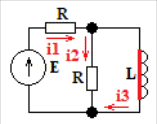 i1(0-) = i3(0-) = E/R = 210/80 = 2,625 A i2(0-) = 0 t(∞). 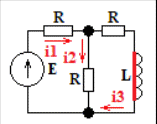 i1(∞) = E/(R + R/2)= 210/120 = 1,75 A i2(∞) = i3(∞) = i1(∞)/2 = 0,875 A t(0+). При размыкании ключа по второму закону коммутации i3(0-) = i3(+) i3(0) = 2,625 A Кирхгоф: i1 - i2 - i3 = 0 R*i1 + R*i2 = E -R*i2 + R*i3 + uL = 0 Кирхгофдлямомента 0+: i1 - i2 - i3 = 0 → i1 = i2 + 2,625 = 2,625 A 80*i1 + 80*i2 = 250 → 80*(i2 + 2,625) + 80*i2 = 210 80*i2 + 210 + 80*i2 = 210 → i2 = 0 i3(0+) = 2,625 A i2(0+) = 0 i1(0+) = 2,625 A 2. Характеристическоеуравнение: 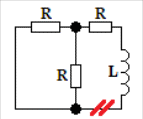 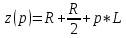 = 120 + p*0,6 = 0 = 120 + p*0,6 = 0p = -120/0,6 = -200 Корень один, действительный следовательно решение для свободной составляющей должно иметь вид А* 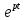 . .В итоге: i1(t) = i1пр + A1* 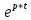 = 1,75 + А1* = 1,75 + А1*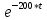 Постоянную интегрирования Аu находим из начальных условий при t = 0+. Она равна свободной составляющей: А1 = i1св = i1(0+) - i1пр = 2,625 - 1,75 = 0,875 А Тогда окончательно i1(t) = 1,75 + 0,875* 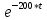 В В3. Аналогично для остальных переменных: А2 = i2св = i2(0+) - i2пр = 0 - 0,875 = -0,875 A i2(t) = -0,875* 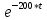 А АА3 = i3св = i3(0+) - i3пр = 2,625 - 0,875 = 1,75 A i3(t) = 0,875 + 1,75* 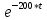 A AУчтем, что: uL(t0 = L*i3(t)' = 0,6*(0,875 + 1,75* 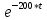 )' = 0,6*1,75*(-200)* )' = 0,6*1,75*(-200)*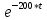 = == -210* 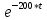 В В |
