пися. Расчетная схема рамы представлена на рис. 1, основная и эквивалентная системы на рис. 2, 3 соответственно

• Название: Расчетная схема рамы представлена на рис. 1, основная и эквивалентная системы на рис. 2, 3 соответственно
• Дата: 23.05.2022
• Размер: 124.34 Kb.
• Имя файла: 1.docx
• Тип: Документы; #546045

Расчетная схема рамы представлена на рис. 4.1, основная и эквивалентная системы – на рис. 4.2, 4.3 соответственно.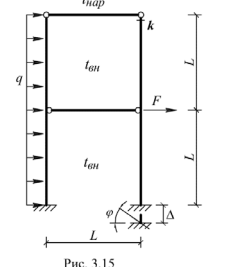



Силы X₁ и X₂ определяются из условий отсутствия взаимного перемещения концов стержней, сходящихся в шарнире (узел 2). Эти условия записываются в форме канонических уравнений метода сил:

 (4.1)

В первом уравнении написано, что перемещение по вертикали, а во втором – по горизонтали равны нулю.

Свободные члены уравнений ₁ и ₂ определяются от каждого воздействия отдельно.

4.1. Определение коэффициентов канонических уравнений

Определение _ik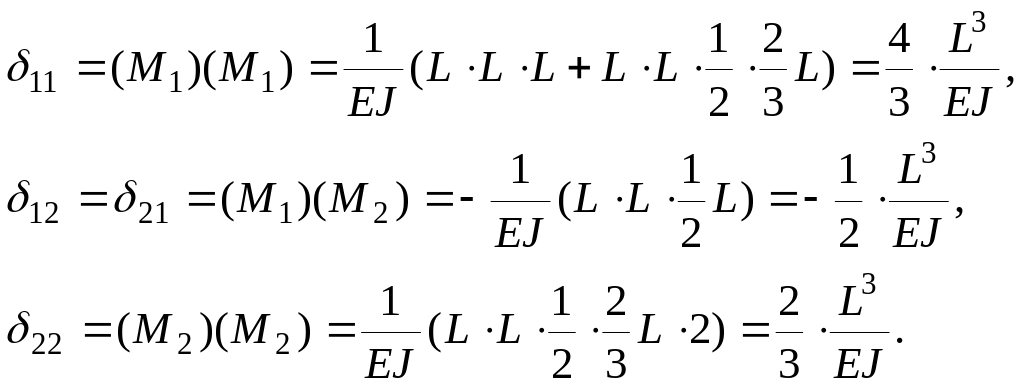

Вид деформированной основной системы от единичных воздействий представлен на рис. 4.1.1 и 4.1.2, эпюры (М₁) и (М₂) – на рис. 4.1.3, 4.1.4 соответственно.



Проверка правильности вычисления коэффициентов выполняется с помощью суммарной единичной эпюры (М_S), представленной на рис. 4.1.5.





_ik вычислены верно.

Определение свободных членов ₁ и ₂ от силового воздействия

Вид деформированной основной системы от силового воздействия представлен на рис. 4.1.6, эпюры (М_F) – на рис. 4.1.7.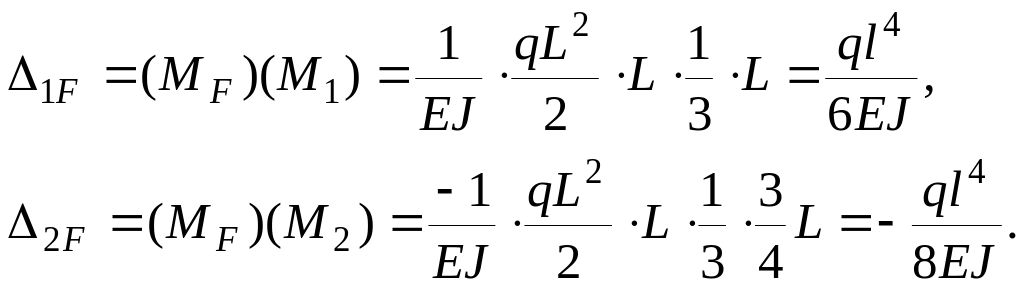



Проверка правильности вычисления коэффициентов выполняется с помощью суммарной единичной эпюры (М_S), представленной на рис. 4.1.5.



_1F и _2F вычислены верно.

Определение свободных членов ₁ и ₂ от температурного воздействия

Вид деформированной основной системы от температурного воздействия представлен на рис. 4.1.8, единичные эпюры (N₁) и (N₂) – на рис. 4.1.9, 4.1.10 соответственно.

В этом случае формула для определения перемещений имеет вид:



В нашем примере получаем: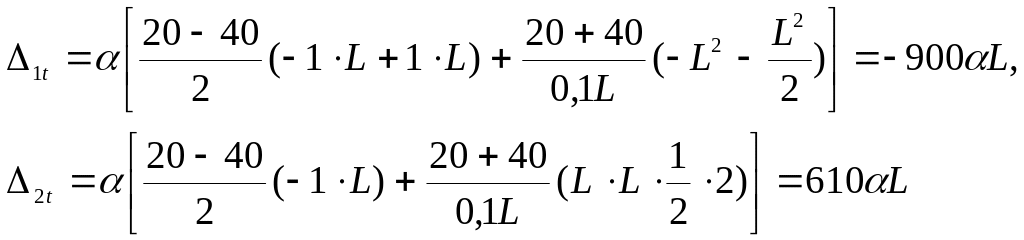



Определение свободных членов ₁ и ₂ от кинематического воздействия

Вид деформированной основной системы от кинематического воздействия представлен на рис. 4.1.11.

В этом случае формула для определения перемещений имеет вид:



В нашем примере получаем: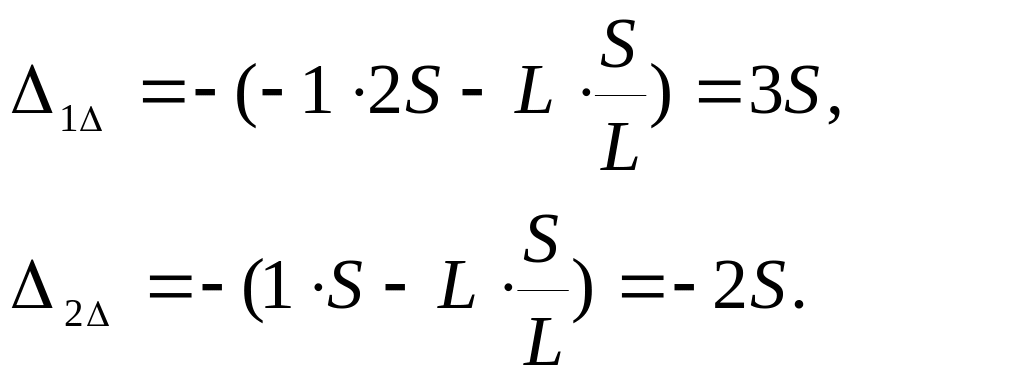