RGR_2Кукушкин. Расчётнографическая работа 2 Случайные величины
 Скачать 43.24 Kb. Скачать 43.24 Kb.
|
|
Федеральное государственное бюджетное образовательное учреждение Высшего образования «Чувашский государственный университет имени И.Н.Ульянова» Расчётно-графическая работа №2 Случайные величины Вариант 11 Выполнил студент группы МС-11-16 Кукушкин Н.Ю. Проверила: Селивёрстова Л.В Чебоксары 2018 Задача 2.1. В каждом из 11 независимых испытаний событие А происходит с постоянной вероятностью 0,41. Вычислить все вероятности рk , k = 0, 1, 2, ..., 11, где k - частота события А. Построить график вероятностей рk. Вычислить наивероятнейшую частоту. 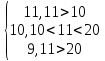 Задано: n = 11, p = 0,41, q = 1 - p = 0,59. Найти: 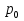 , , 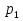 , , 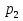 , ..., , ..., 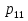 и k. и k.Значение 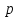 вычисляем по формуле Бернулли вычисляем по формуле Бернулли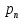 (k)= (k)=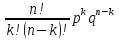 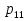 (k=0)= (k=0)=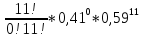 =1*1*0,000607=0,003016 =1*1*0,000607=0,003016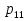 (k=1)= (k=1)=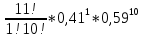 =11*0,41*0,005111=0,023051 =11*0,41*0,005111=0,023051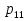 (k=2)= (k=2)=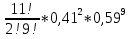 =55*0,1681*0,008663=0,080094 =55*0,1681*0,008663=0,080094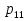 (k=3)= (k=3)=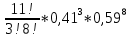 =165*0,0689*0,0147=0,167117 =165*0,0689*0,0147=0,167117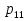 (k=4)= (k=4)=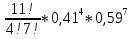 =330*0,0282*0,0249=0,231719 =330*0,0282*0,0249=0,231719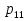 (k=5)= (k=5)=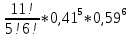 =462*0,0116*0,0422=0,226158 =462*0,0116*0,0422=0,226158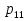 (k=6)= (k=6)=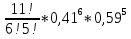 =462*0,0047*0,0715=0,155255 =462*0,0047*0,0715=0,155255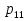 (k=7)= (k=7)=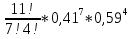 =330*0,0019*0,1212=0,075992 =330*0,0019*0,1212=0,075992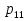 (k=8)= (k=8)=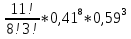 =165*0,0008*0,2054=0,027113 =165*0,0008*0,2054=0,027113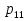 (k=9)= (k=9)=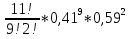 =55*0,0003*0,3481=0,005744 =55*0,0003*0,3481=0,005744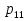 (k=10)= (k=10)=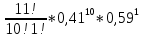 =11*0,0001*0,59=0,000649 =11*0,0001*0,59=0,000649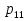 (k=11)= (k=11)=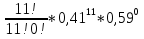 =1*0,000055*1=0,000055 =1*0,000055*1=0,000055Найдем наивероятнейшую частоту по заданным условиям: np - q k np + p 11*0,41-0,59k11*0,41+0,41 3,92k4,92 K=4
Задача 2.2. В каждом из 755 независимых испытаний событие А происходит с постоянной вероятностью 0,57. Найти вероятность того, что событие А происходит: а) точно 325 раз; б) меньше чем 325 и больше чем 274 раз; в) больше чем 325 раз Решение: a)Задано: п = 755, р = 0,57, k = 325 Найти: 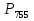 (325) (325)Используем локальную теорему Лапласа . Находим: 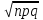 = =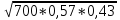 =13,1 =13,1X= 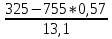 =-8 =-8(-8) = 0 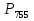 (325)=0 (325)=0б) Задано: п = 755, р = 0,57,а=274, k = 325 Найти: 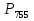 (274 (274Используем интегральную формулу Лапласа 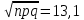 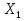 = =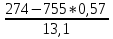 =-11.9 =-11.9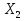 = =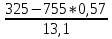 =-8 =-8Значения функции Ф(х) найдем из таблицы: 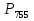 (274 (274в) Задано: n = 755, р = 0,57, а = 325, b = 755. Найти: 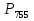 (325 (325Имеем 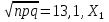 =-8 =-8 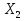 = =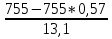 =24,8 =24,8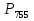 (325 (325Задача 2.3. В каждом из 588независимых испытаний событие А происходит с постоянной вероятностью 0,51. Найти вероятность того, что событие А происходит: а) точно 308 раз; б) точно 278 раз; в) меньше чем 339 и больше чем 279 раз; г) меньше чем 323 раз. При решении этой задачи используем теоремы Лапласа: локальную в случаях а) и б) и интегральную для случаев в) и г). а)X= 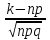 = =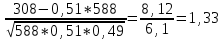 (1,33) =0,1647 (1,33) =0,1647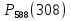 = =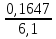 =0,027 =0,027б) X= 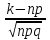 = =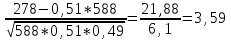 (3,59) =0,0006 (3,59) =0,0006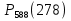 = =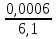 =0,000098 =0,000098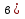 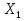 = =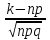 = =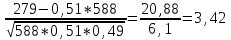 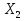 = =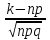 = =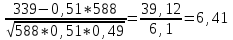 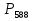 (279 (279в) 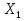 = =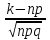 = =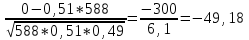 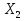 = =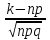 = =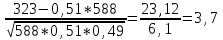 9 9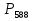 (0 (0Задача 2.4. На телефонной станции неправильное соединение происходит с вероятностью 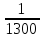 . Найти вероятность того, что среди 1300 соединений имеет место: . Найти вероятность того, что среди 1300 соединений имеет место: а) точно 3 неправильных соединений; б) меньше чем 3 неправильных соединений; в) больше чем 2 неправильных соединений. Решение а) Задано: n = 1300, p = 1/1300, k = 3. Найти: 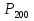 (3). (3). Получаем: = 3900*1/1300 = 3. Из таблиц определяем Р200(1) = 0,3679. 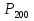 (k=3)= (k=3)=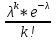 = =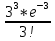 = =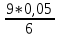 =0,075 =0,075б) 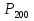 (k<3)= (k<3)=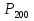 (k=0)+ (k=0)+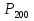 (k=1)+ (k=1)+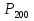 (k=2)= (k=2)=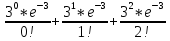 =0,05+0,15+0,225=0,425 =0,05+0,15+0,225=0,425в) Эту задачу можно решить проще- найти вероятность противоположного события, так как в этом случае нужно вычислить меньше слагаемых. Принимая во внимание предыдущий случай, имеем 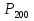 (k>2)=1- (k>2)=1- 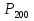 (k≤2)=1- (k≤2)=1-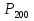 (k<3)=1-0,425=0,575 (k<3)=1-0,425=0,575Задача 2.5. В каждом из 490 независимых испытаний событие А происходит с постоянной вероятностью 0,74. Найти вероятность того, что относительная частота k/ 490 этого события отличается по абсолютной величине от вероятности 0,74 не больше чем на 0,0033 (на 0,0088) Задано: n = 490, р = 0,74, 1=0,0044, 2 = 0,0088. Найти: 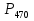 (k/ 490 - 0,74< 0,0044) и (k/ 490 - 0,74< 0,0044) и 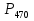 (k/ 490 - 0,74< 0,0088). (k/ 490 - 0,74< 0,0088).Решение 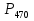 (k/ 490 - 0,74< 0,0044)= 2Ф(0,0044 (k/ 490 - 0,74< 0,0044)= 2Ф(0,0044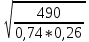 ) =2Ф(0,22) =2*0,0871=0,1742 ) =2Ф(0,22) =2*0,0871=0,1742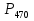 (k/ 490 - 0,74< 0,0088)= 2Ф(0,0088 (k/ 490 - 0,74< 0,0088)= 2Ф(0,0088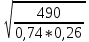 ) =2Ф(0,44) =2*0,17=0,34 ) =2Ф(0,44) =2*0,17=0,34Задача 2.6. Случайная величина Х задана рядом распределения.
Найти функцию распределения F(x) случайной величины Х и построить ее график. Вычислить для Х ее среднее значение ЕХ, дисперсию DX и моду Мо. Решение Функцию распределения находим по формулам (1.20) и (1.21) для дискретных случайных величин: 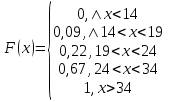 Построим график функции распределения F(x). Среднее значение ЕХ вычисляем по формуле : ЕХ = 14 * 0,09 + 19 * 0,13 + 24 * 0,45 + 34 * 0,33 = 25,75. Для нахождения дисперсии воспользуемся формулами : Е( 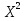 ) = ) = 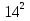 * 0,09 + * 0,09 + 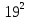 * 0,13 + * 0,13 + 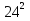 * 0,45 + * 0,45 + 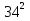 * 0,33 = 705,25, * 0,33 = 705,25, DX = 705,25- 25,75 = 679,5 Модой Мо(Х) дискретной случайной величины называют ее наиболее вероятное значение: Мо(Х) = 24 Задача 2.7. Случайная величина Х задана функцией плотности вероятности 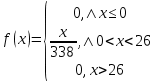 Найти функцию распределения F(x) случайной величины Х. Построить график функции f(x) и F(x). Вычислить для Х ее среднее значение ЕХ, дисперсию DX, моду Мо и медиану Ме. Решение Функцию распределения F(х) непрерывной случайной величины найдем по формуле: F(x)= 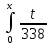 dt= dt=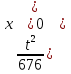 = =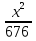 , 0 , 0Поэтому 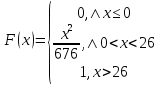 Построить графики функций f(x) и F(x). Среднее значение Х вычисляем по формуле EX= 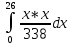 = =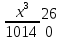 = =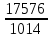 =17,3 =17,3Для нахождения дисперсии Х воспользуемся формулами: E 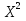 = =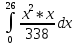 = =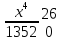 = =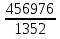 =338 =338DX = 338 - 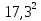 = 338-299 = 39 = 338-299 = 39Из графика видно, что f(x) достигает максимума в точке х = 26 и, значит Мо =26. Для нахождения медианы Ме нужно решить уравнение 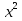 = 338. = 338. Имеем х = 13 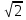 . Случайная величина определена только на интервале [0, 26], значит, Ме = 13 . Случайная величина определена только на интервале [0, 26], значит, Ме = 13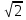 = 18,385. = 18,385.Задача 2.8. Случайная величина Х задана функцией распределения 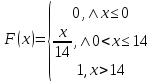 Найти функцию плотности вероятности f(x) случайной величины Х. Построить график функции f(x) и F(x). Вычислить для Х ее среднее значение ЕХ, дисперсию DX, моду Мо и медиану Ме. Решение Функциюплотности f(х) непрерывной случайной величины найдем по производной: f(x)=F’(x)= 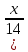 )’= )’=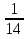 Поэтому 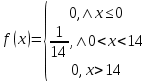 Построить графики функций f(x) и F(x). Среднее значение Х вычисляем по формуле EX= 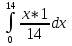 = =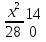 = =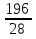 =7 =7Для нахождения дисперсии Х воспользуемся формулами: E 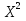 = =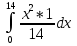 = =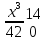 = =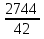 =65,3 =65,3DX = 65,3 - 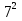 = 65,3-49 = 16,3 = 65,3-49 = 16,3Из графика видно, что f(x) достигает максимума в точке х принадлежит 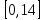 и, значит и, значитМо – любое число на отрезке 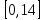 0,5=Р(0 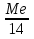 → Me=7. → Me=7.Задача 2.9. Задана случайная величина ХN (3, 11). Найти вероятность того, что эта случайная величина принимает значение : а) в интервале [8, 17]; б) меньшее 8; в) большее 17; г) отличающееся от своего среднего значения по абсолютной величине не больше чем на 3. Решение В первых трех случаях можно воспользоваться формулой Р(a ≤X≤ b )=Ф 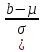 )-Ф( )-Ф(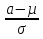 ), ),а в четвёртом формулой Р( 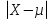 ≤ε)=2Ф( ≤ε)=2Ф(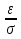 ) )а) Р(8 Х 17)=Ф( 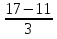 )-Ф( )-Ф(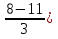 =Ф(2)+Ф(1)=0,4772+0,3413=0,8185 =Ф(2)+Ф(1)=0,4772+0,3413=0,8185б) Р(Х 8)= Р( 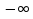 Х 8)=Ф( Х 8)=Ф(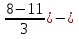 Ф( Ф(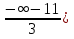 =Ф(-1)+0,5= -0,3413+0,5=0,1587 =Ф(-1)+0,5= -0,3413+0,5=0,1587в) Р(Х 17)=Р(17Х+ 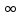 )=Ф(+ )=Ф(+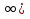 -Ф( -Ф(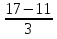 )=0,5-Ф(2)=0,5-0,4772=0,0228 )=0,5-Ф(2)=0,5-0,4772=0,0228г) Р( 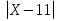 ≤3)=2Ф( ≤3)=2Ф(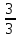 )=2Ф(1)=2*0,3413=0,6826 )=2Ф(1)=2*0,3413=0,6826Задача 2.10. Задана случайная величина 1,5 . и точки х1 , х2, х3, х4, х5 на числовой оси, разделяющие ее на на шесть интервалов. Найти вероятность того, что случайная величина Х принимает значения в этих интервалах Решение Вероятность того, что нормально распределенная случайная величина Х приняла значение из интервала , определяется по следующей формуле: Р(a ≤X≤ b )=Ф 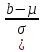 )-Ф( )-Ф(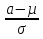 ) )Р(Х -9)= Ф( 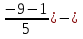 Ф( Ф(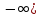 =Ф(-2)+0,5= -0,4772+0,5=0,0228 =Ф(-2)+0,5= -0,4772+0,5=0,0228Р(-9 Х -6)=Ф( 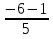 )-Ф( )-Ф(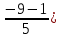 =Ф(-1,4)-Ф(-2)=-0,4192+0,4772=0,0580 =Ф(-1,4)-Ф(-2)=-0,4192+0,4772=0,0580Р(-6 Х 1)=Ф( 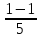 )-Ф( )-Ф(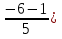 =Ф(0)-Ф(-1,4)=0 +0,4192=0,4192 =Ф(0)-Ф(-1,4)=0 +0,4192=0,4192Р(1 Х 6)=Ф( 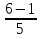 )-Ф( )-Ф(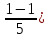 =Ф(1)-Ф(0)=0,3413-0=0,3413 =Ф(1)-Ф(0)=0,3413-0=0,3413Р(6 Х 16)=Ф( 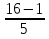 )-Ф( )-Ф(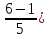 =Ф(3)-Ф(1)=0,49865-0,3413=0,15735 =Ф(3)-Ф(1)=0,49865-0,3413=0,15735Р(Х 16)=Ф(+ 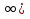 -( -(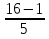 )=0,5-Ф(3)=0,5-0,49865=0,00135 )=0,5-Ф(3)=0,5-0,49865=0,00135Проверка: Р( 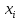 Х Х 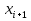 + 1)=1 + 1)=10,0228+0,0580+0,4192+0,3413+0,15735+0,00135=1 |