Электротехника. Расчетнографическая работа 2
 Скачать 1.69 Mb. Скачать 1.69 Mb.
|
|
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 2 Вариант №54. Рассчитать цепь, изображенную на рисунке 1, в которой E5 = 141еj45; J1 = 3ej45; f = 50 Гц. Параметры пассивных элементов: R2 = R4 = 277 Oм; R1 =R3 = R5 = 744,5 Oм; L3 = 834,5 мГн; XL3 = 2fL3 = 265.166 Ом; C5 = 804,5 мкФ; XC5 = 1/(2fC5) = 3.957 Ом; Число узлов n = 3. Число независимых контуров p = 3. 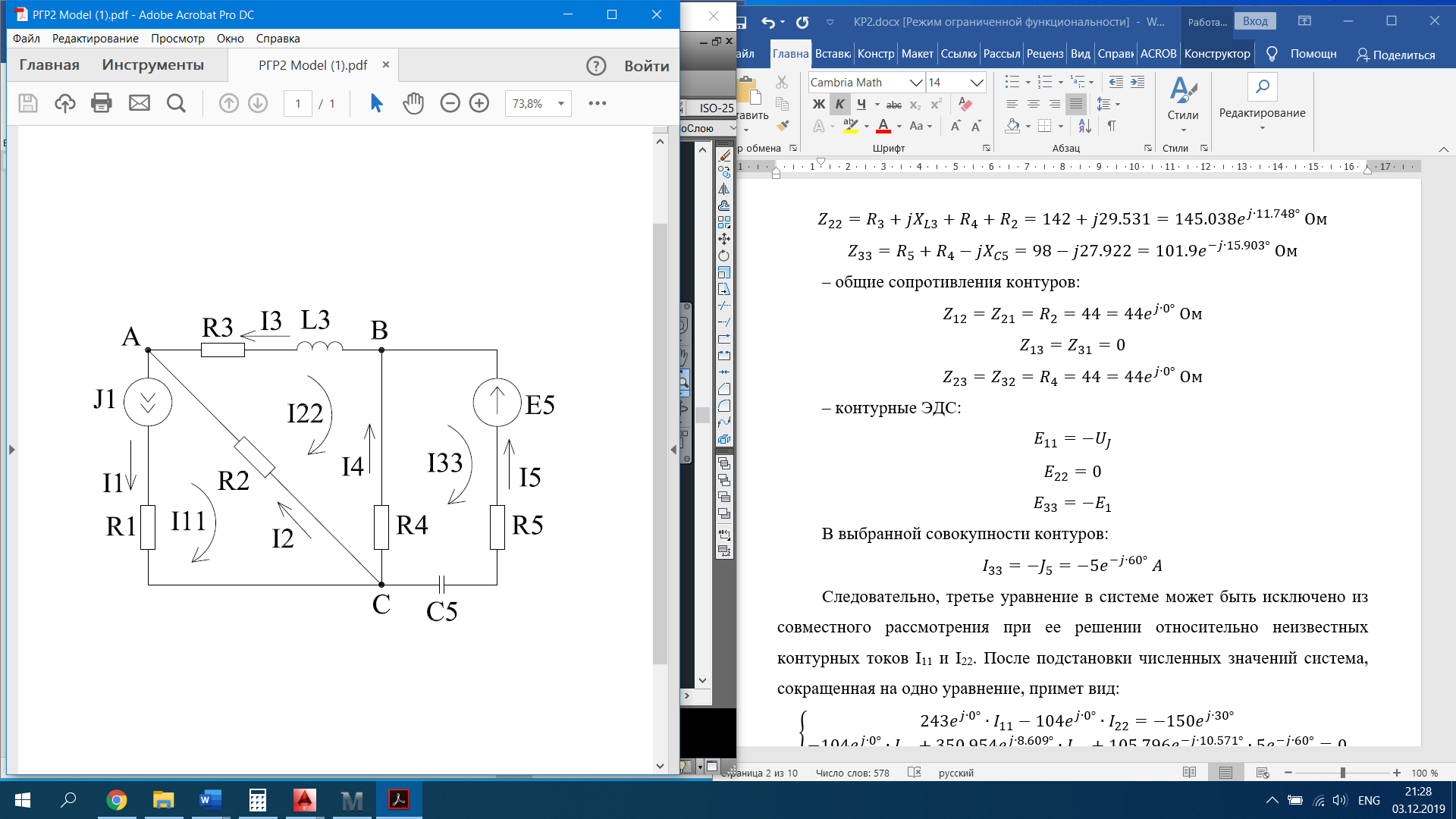 Рисунок 1 1. Составление системы уравнений Кирхгофа Произвольно задавшись положительным направлением токов ветвей (см. рис. 1) и совокупностью независимых контуров, запишем: – уравнения по I закону Кирхгофа, число уравнений (n – 1) = 3 – 1 = 2 узел А : 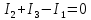 ; ;узел В: 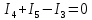 ; ;– уравнения по II закону Кирхгофа, число уравнений p = 3: I контур: 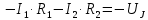 II контур: 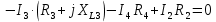 III контур: 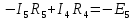 В результате имеем систему, состоящую из 5 уравнений, разрешимую относительно 5 неизвестных: 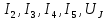 2. Решение методом контурных токов Для рассматриваемой цепи (см. рис. 1) система уравнений относительно контурных токов I11, I22, I33, совпадающих по направлению с обходом контуров, имеет вид 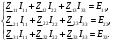 В данной системе: – собственные сопротивления контуров: 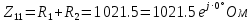 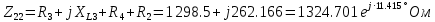 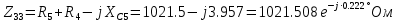 – общие сопротивления контуров: 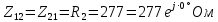 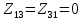 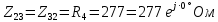 – контурные ЭДС: 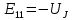 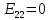 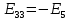 В выбранной совокупности контуров: 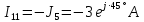 Следовательно, первое уравнение в системе может быть исключено из совместного рассмотрения при ее решении относительно неизвестных контурных токов I11 и I22. После подстановки численных значений система, сокращенная на одно уравнение, примет вид: 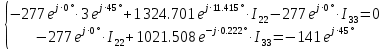 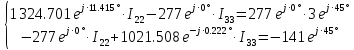 Решать данную систему целесообразно с применением правила Крамера. Определители системы: 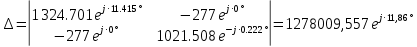 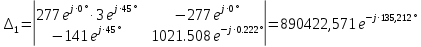 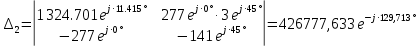 Токи I22 и I33 находят по формулам: 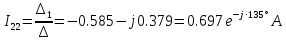 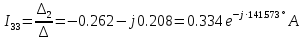 В соответствии с условно принятыми положительными направлениями (см. рис. 1) вычислим токи ветвей: 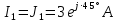 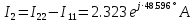 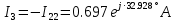 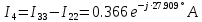 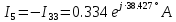 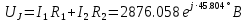 Мгновенные значения токов ветвей и напряжения на источнике тока Поскольку угловая частота равна = 2f, а амплитуда связана с действующим значением с помощью соотношения 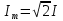 , следовательно, , следовательно,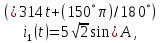 где  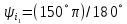 начальная радиан-фаза тока i1 начальная радиан-фаза тока i1аналогично запишем: 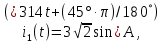 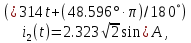 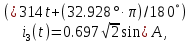 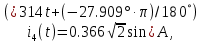 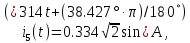 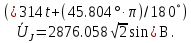 3. Баланс активных и реактивных мощностей Комплексная мощность источников: 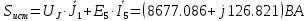 Комплексная мощность потребителей: 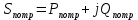 где активная мощность: 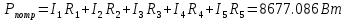 реактивная мощность: 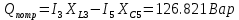 4. Построение топографической диаграммы 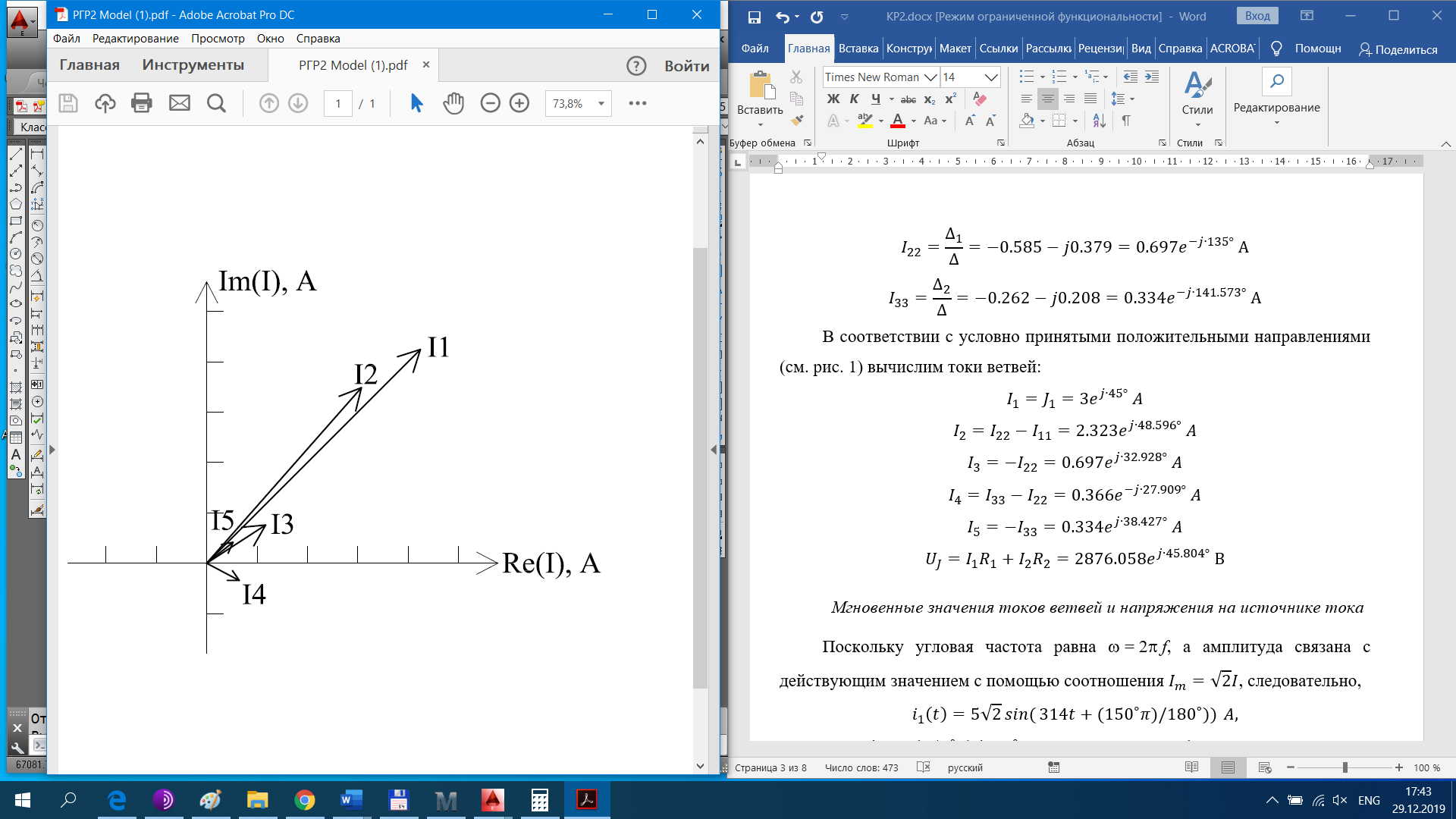 Рисунок 2 На рис. 2 представлена векторная диаграмма токов ветвей рассматриваемой схемы в соответствии с масштабом по току МI: 1 деление – 0.5 А. Диаграмма токов позволяет проверить графическим путем выполнение соотношений по I закону Кирхгофа. В соответствии с принятыми на рис. 1 обозначениями рассчитываются значения потенциалов точек цепи. Потенциал точки А принимается равным нулю. 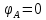 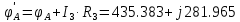 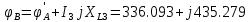 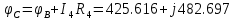 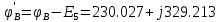 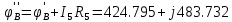 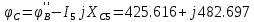 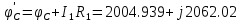 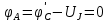 Выбираем масштаб по напряжению МU для построения диаграммы: 1 деление – 50 В. 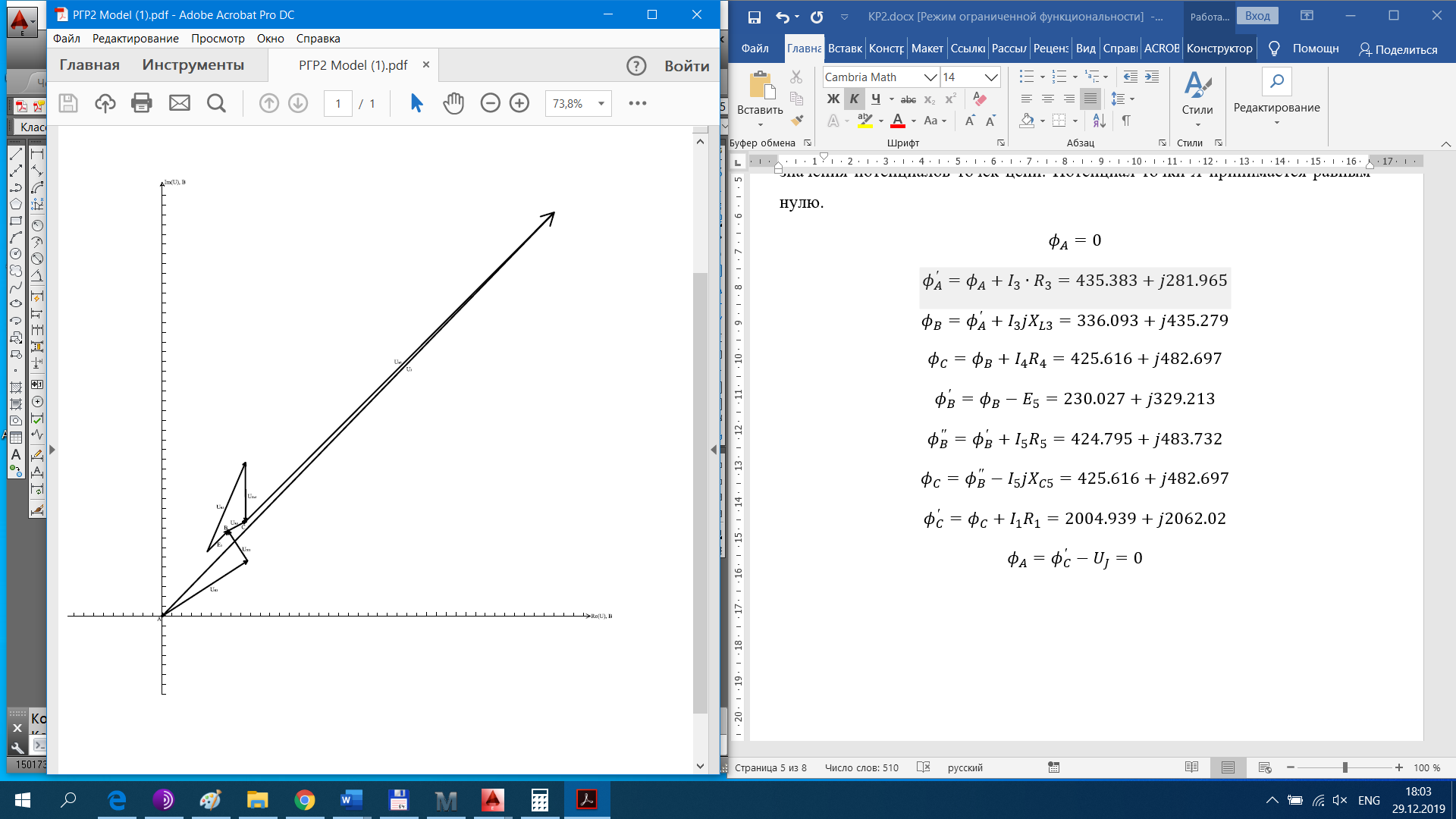 5. Метод узловых потенциалов Для рассматриваемой цепи (рис. 1), содержащей 3 узла, система, составленная в соответствии с методом узловых потенциалов, должна содержать 2 уравнения. Выберем в качестве опорного узел A. Имеем: 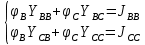 Собственные узловые проводимости: 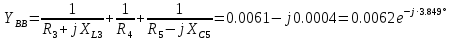 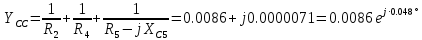 общие узловые проводимости: 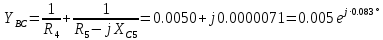 узловые токи: 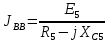 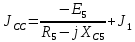 Тогда система уравнений будет выглядеть как: 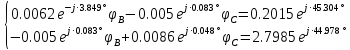 Решая систему уравнений, получим: 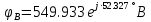 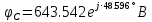 Найдем токи в ветвях: 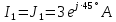 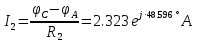 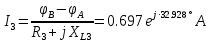 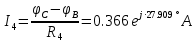 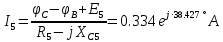 Полученные значения не отличаются от значений, полученных методом контурных токов. 6. Метод наложения С использованием принципа суперпозиции рассчитывается ток I5. Поскольку в цепи два источника, для определения искомого тока строятся две подсхемы, каждая из которых содержит только один из источников, а второй исключается. Расчет составляющей I5’ по схеме (рис. 4). 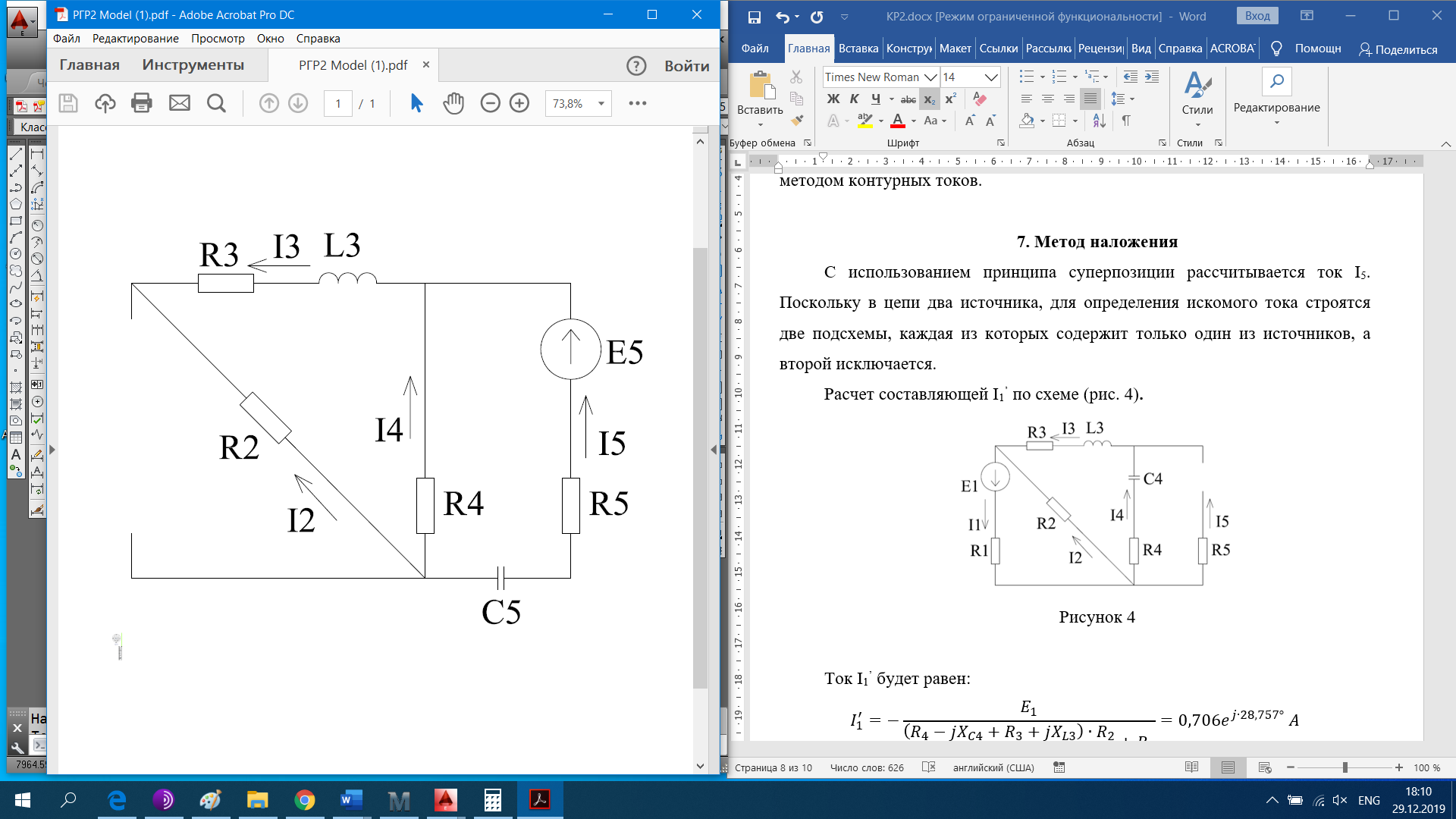 Рисунок 4 Ток I5’ будет равен: 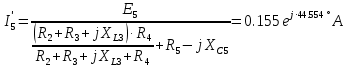 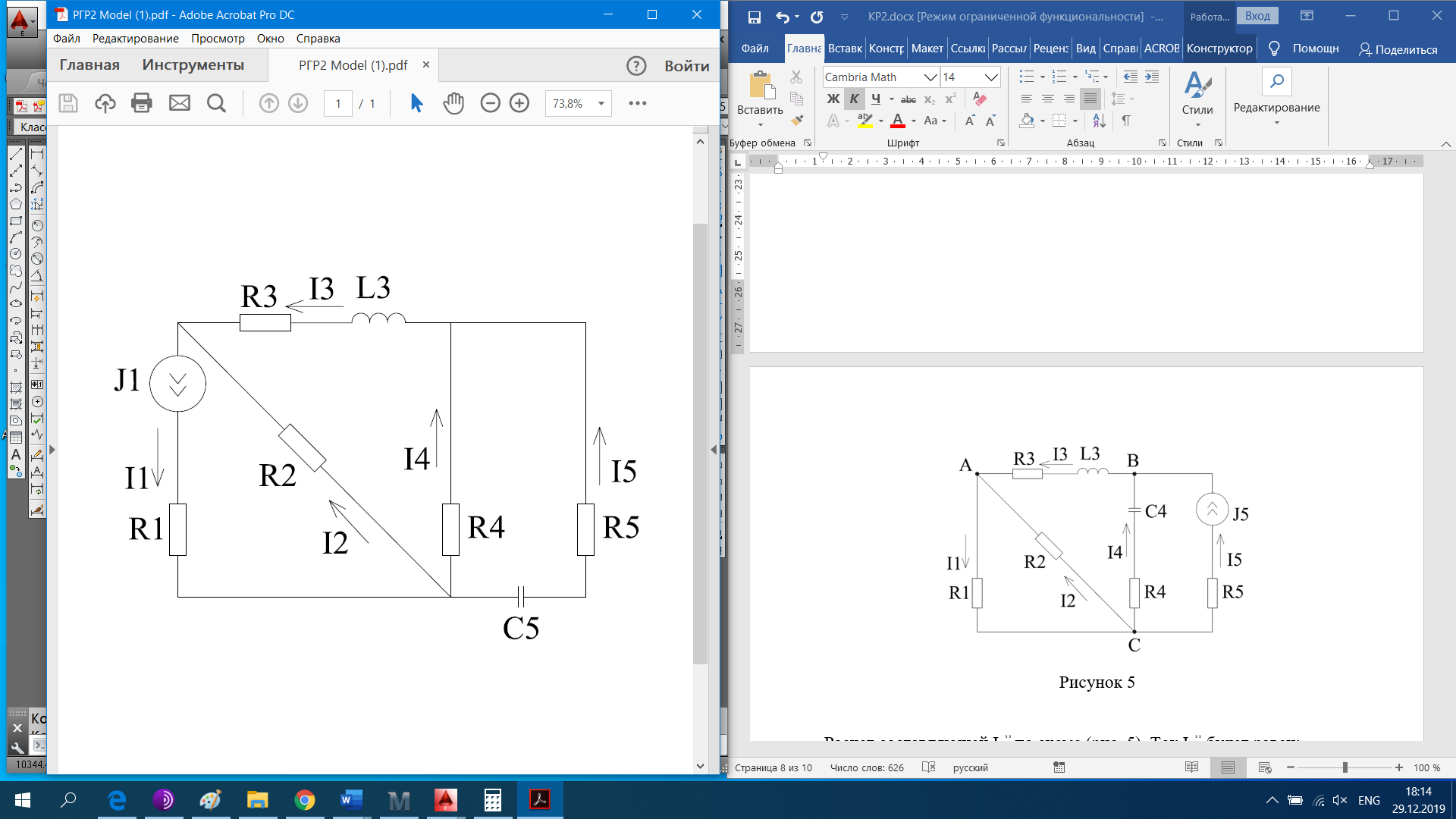 Рисунок 5 Расчет составляющей I5’’ по схеме (рис. 5). Ток I5’’ будет равен: 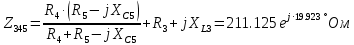 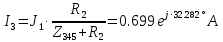 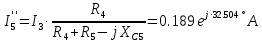 Искомый ток: 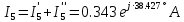 7. Метод эквивалентного генератора С использованием теоремы об активном двухполюснике определяется ток I5. 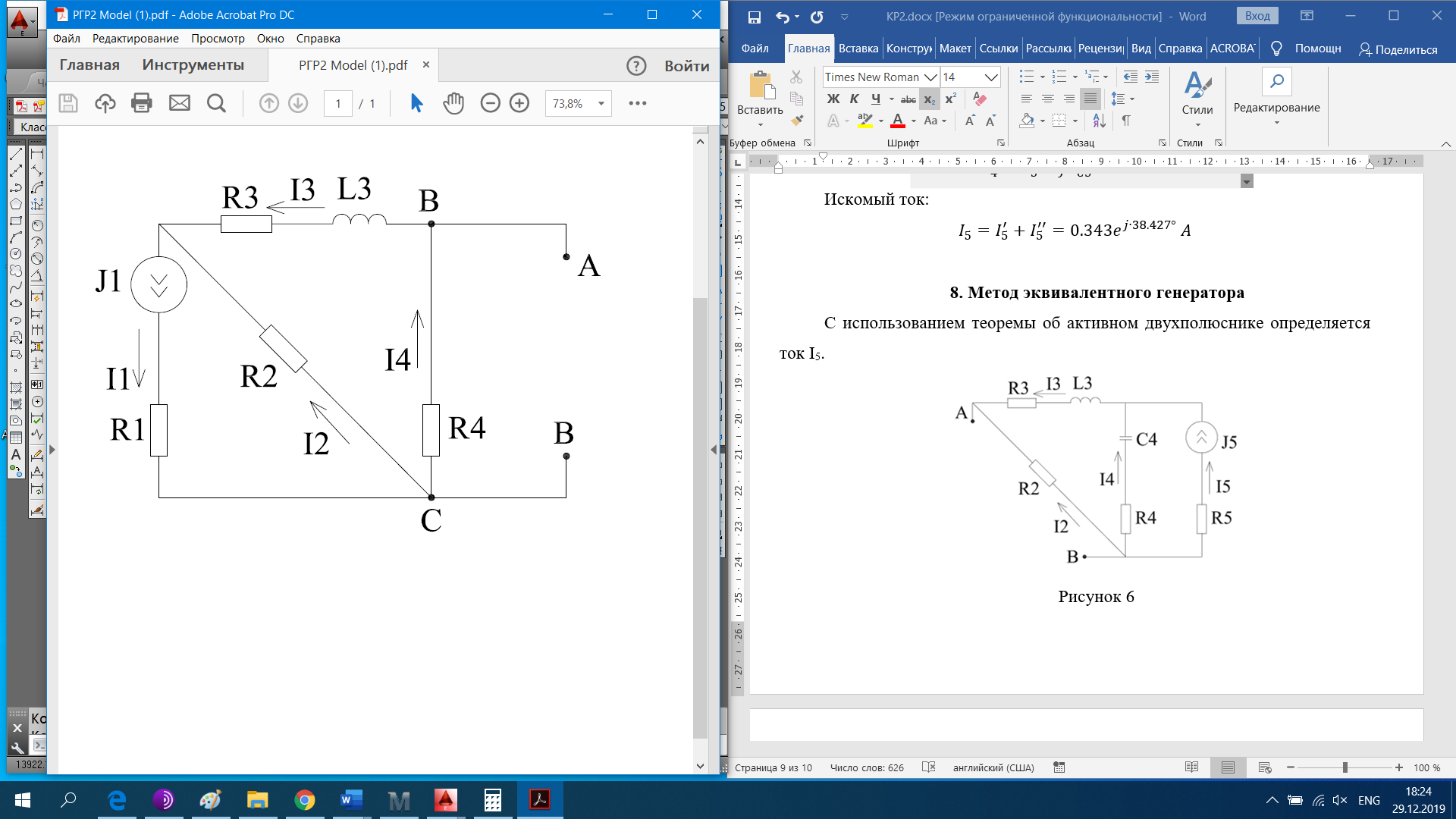 Рисунок 6 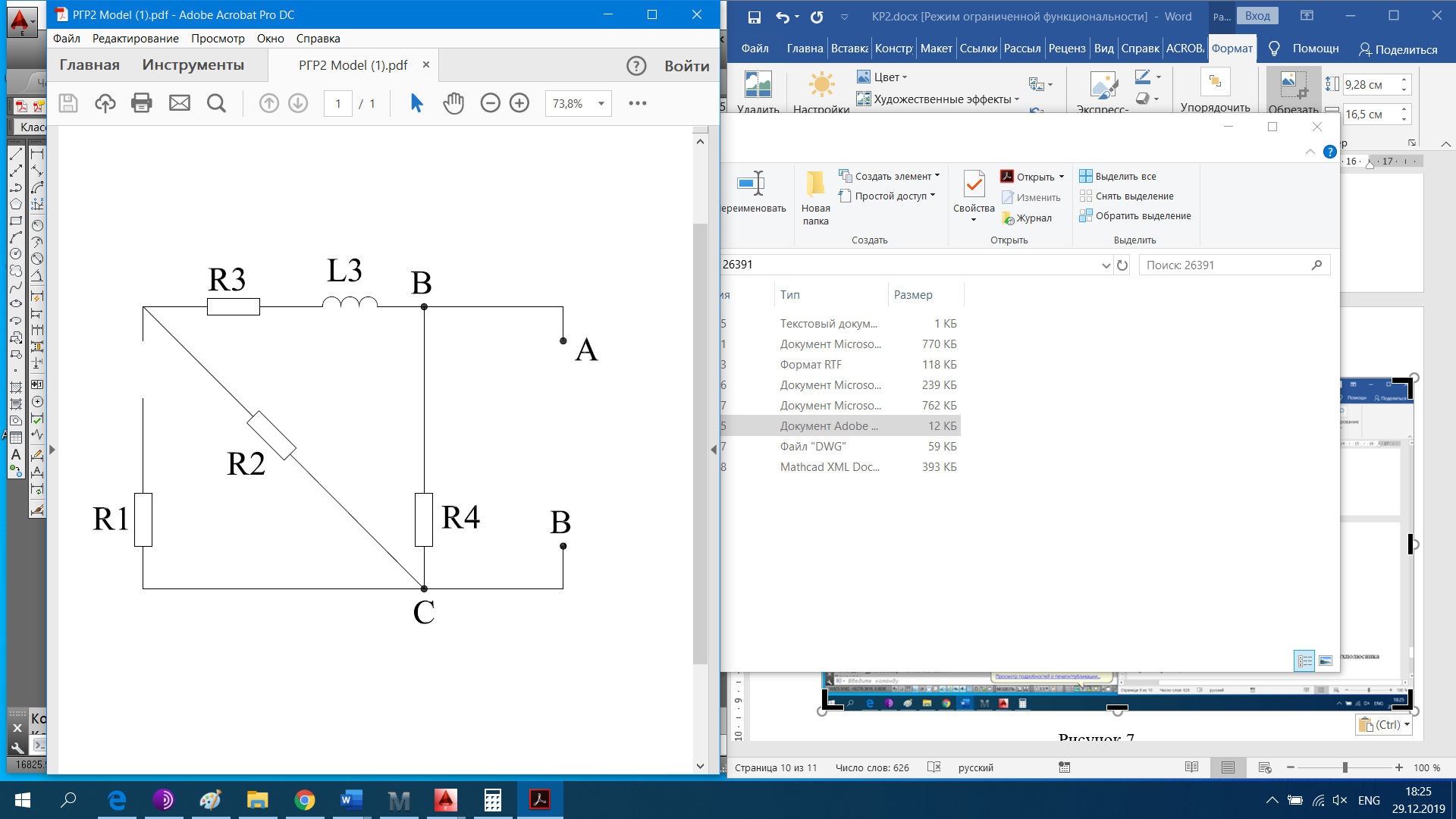 Рисунок 7 Напряжение холостого хода на зажимах активного двухполюсника равно (рис. 6): 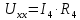 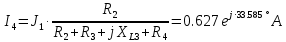 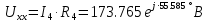 Определение входного сопротивления пассивного двухполюсника (рис. 7). 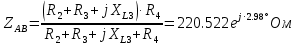 Искомый ток: 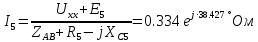 |
