Расчетнографическая работа 3 Расчет переходных процессов в линейных цепях
 Скачать 230.73 Kb. Скачать 230.73 Kb.
|
 Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра теоретических основ электротехники Расчетно-графическая работа №3 Расчет переходных процессов в линейных цепях Выполнил: студент гр.Группа Фамилия И. О. студента Проверил: преподаватель Ф. И. О. преподавателя Уфа Вариант № 12 Схема №3 R1 = 29 Ом R2 = 80 Ом R3 = 58 Ом R4 = 55 Ом L = 59 мГн C = 55 мкФ E = 108 В Найти 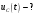 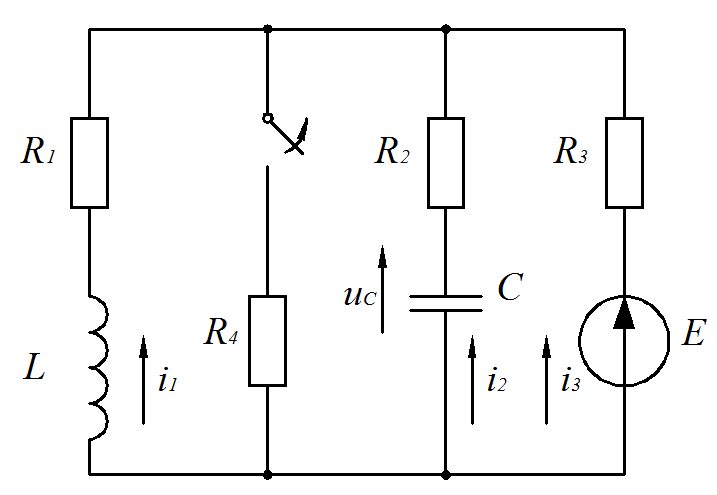 Рис. 1 Исходная схема Задание: Рассчитать закон изменения тока (напряжения) в функции времени классическим методом. Рассчитать закон изменения тока (напряжения) в функции времени операторным методом. На основании полученного аналитического выражения построить график изменения искомой величины в зависимости от времени на интервале от 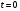 до до 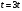 . .Классический метод определения напряжения Искомое напряжение 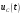 ищем в виде суммы установившегося и свободного напряжения: ищем в виде суммы установившегося и свободного напряжения: 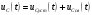 . .Цепь до коммутации: 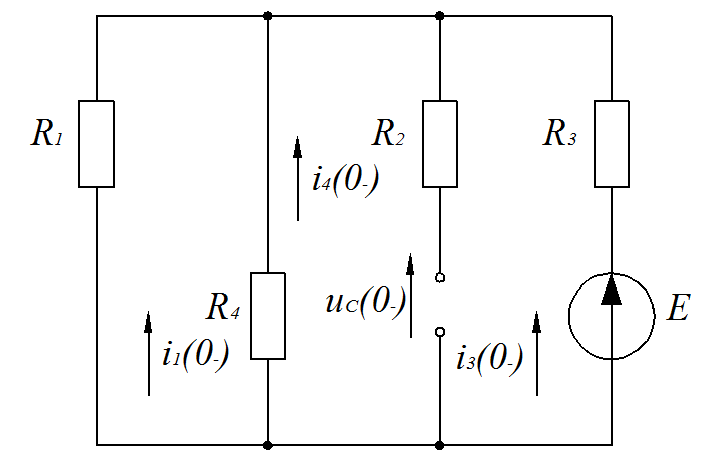 Рис. 2 Цепь до коммутации Независимые начальные условия при 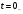 : :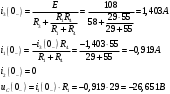 Установившийся режим при t = ∞: 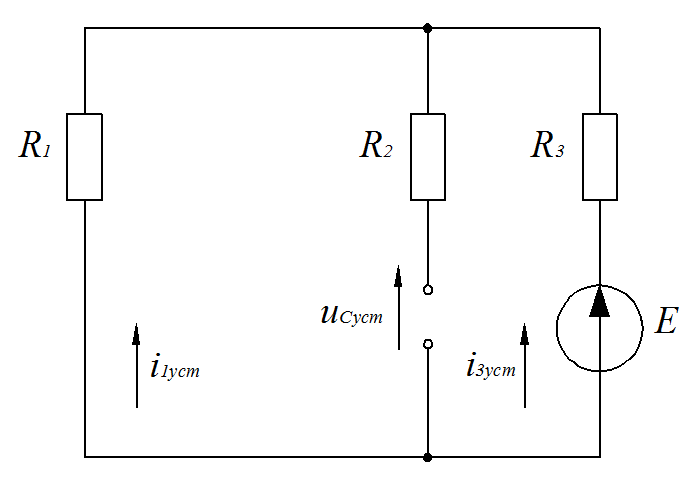 Рис. 3 Цепь в установившимся режиме при t = ∞ 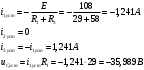 Найдем характеристическое сопротивление цепи 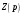 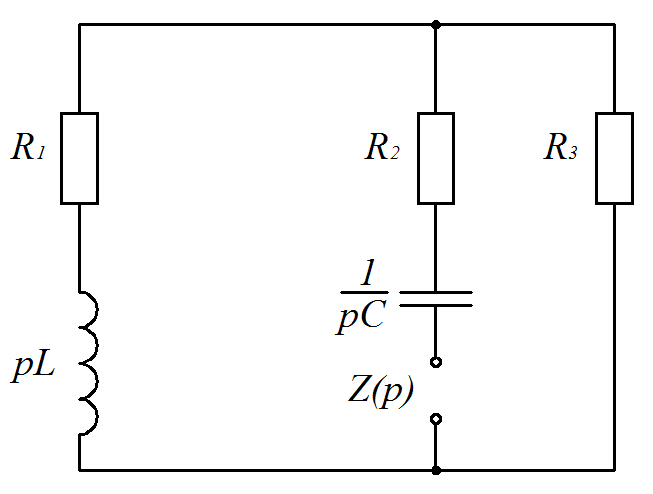 Рис. 4 Схема для определения характеристического сопротивления цепи 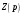 Составим выражение для определения характеристического сопротивления цепи 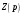 : :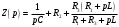 Найдем корни характеристического уравнения для этого приравняем 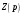 к нулю: к нулю: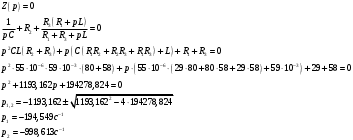 Т.к. корни уравнения вещественные числа, то выражение свободного напряжения примет вид: 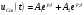 Чтобы найти коэффициенты 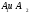 необходимо определить зависимые начальные условия. необходимо определить зависимые начальные условия.Цепь после коммутации: 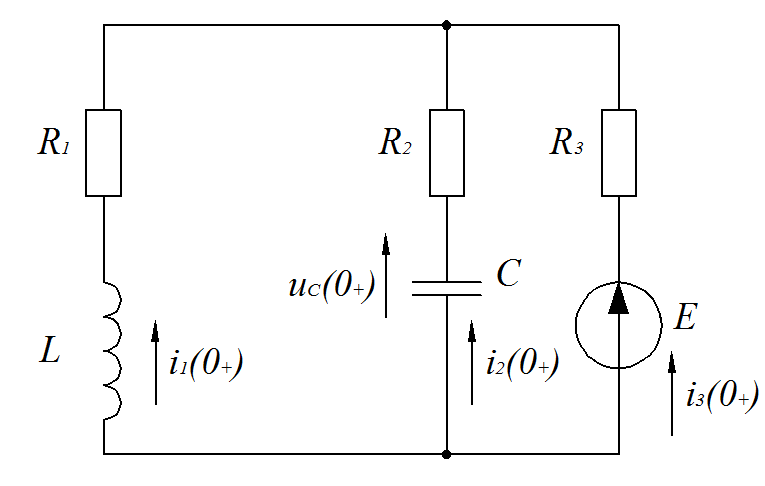 Рис. 5 Цепь после коммутации 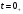 Ток в индуктивных катушках и напряжения на конденсаторах в момент коммутации не изменяются скачками (независимые начальные условия): 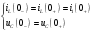 Уравнения Кирхгофа для момента коммутации: 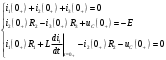 Откуда находим зависимые начальные условия: 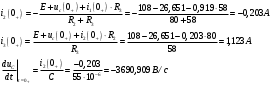 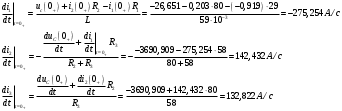 Выражения для искомого напряжения: 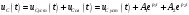 Для определения постоянных интегрирования решим систему из выражений искомого напряжения в момент коммутации и его производной в момент коммутации: 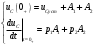 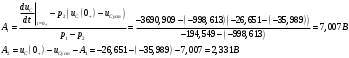 Таким образом, получаем выражение напряжения 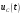 для любого момента времени для любого момента времени  : :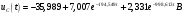 Операторный метод определения напряжения 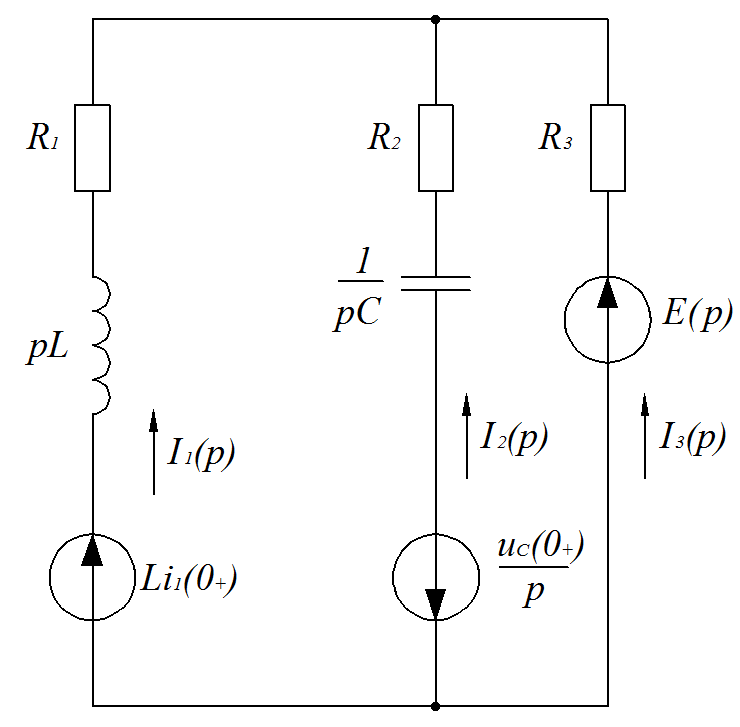 Рис. 6 Схема для операторного метода Независимые начальные условия: 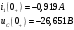 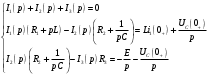 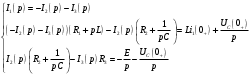 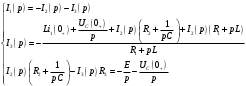 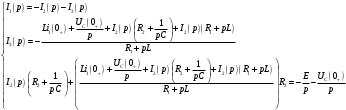 Из третьего уравнения полученной системы уравнений выделим выражение изображения для тока 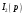 : :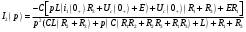 Операторное напряжение на ёмкости следует определять как сумму напряжений непосредственно на сопротивлении 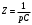 и на внутреннем источнике напряжения и на внутреннем источнике напряжения 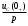 . .Для этого можно воспользоваться обобщенной формой закона Ома: 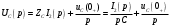 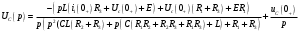 Т.к. изображение искомой величины – сумма отношения двух полиномов 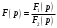 и и 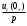 , то для нахождения оригинала по найденному изображению при помощи обратного преобразования Лапласа используем теорему разложения: , то для нахождения оригинала по найденному изображению при помощи обратного преобразования Лапласа используем теорему разложения:Т.к. 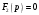 при при 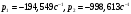 , то , то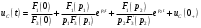 , где , где 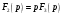 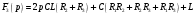 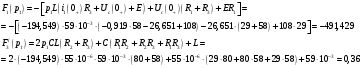  Подставляя полученные значения в исходную формулу для нахождения оригинала, получим искомое значение напряжения: 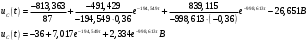 График зависимости напряжения 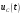 от времени от времени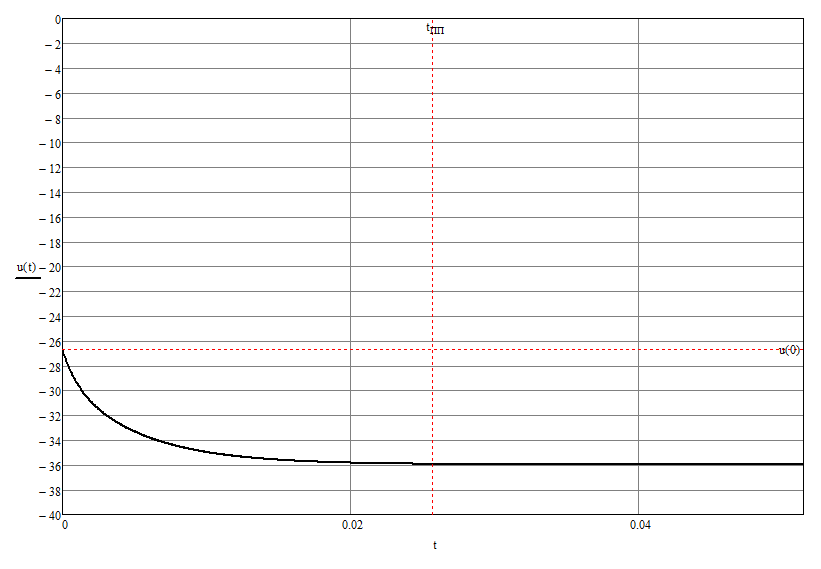 Рис. 7 График функции напряжения 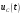 Постоянная времени 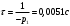 Время переходного процесса 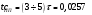 Проверка ответов: "A1": 7,007 "A2": 2,331 "DT1": -275,254 "DT2": 142,432 "DT3": 132,822 "DUC": -3690,909 "I10": -0,919 "I1Y": -1,241 "I20": -0,203 "I30": 1,123 "I3Y": 1,241 "P1": -194,549 "P2": -998,613 "UC0": -26,651 "UCY": -35,989 "Фи": 0 |
