55150. Вар 26. Расчетнографическая работа 5 Переходные процессы в цепях с сосредоточенными параметрами
 Скачать 0.53 Mb. Скачать 0.53 Mb.
|
|
Расчетно-графическая работа № 5 Переходные процессы в цепях с сосредоточенными параметрами Требуется: - рассмотреть переходный процесс в заданной цепи второго порядка с одной ЭДС 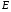 ; ;- определить закон изменения во времени (аналитическое выражение) указанной величины тока или напряжения; - построить график изменения искомой величины в функции времени.  Дано: 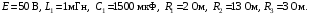 Определить: 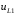 . .Классический метод Размыкание цепи, как задано в условии, не изменяет ток и напряжение на индуктивности, и не возникает переходного процесса. Поэтому решим задачу при замыкании ключа.  Определим сначала ток через индуктивность 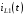 , а затем напряжение на индуктивности , а затем напряжение на индуктивности 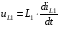 . .1. Расчет установившегося режима до коммутации. Расчет независимых начальных условий.  Определим ток в ветви с индуктивностью и напряжение на емкости 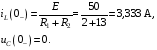 2. Расчет зависимых начальных условий (при 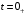 ). ). Составим уравнения по законам Кирхгофа, описывающие состояние цепи после коммутации (при 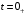 ) )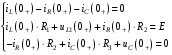 По законам коммутации 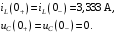 Производная тока ветви с индуктивностью 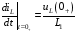 . .Из первого уравнения выразим 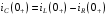 , ,подставим в третье уравнение 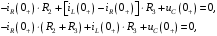 откуда 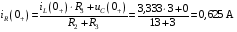 , ,из второго уравнения находим 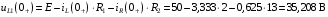 . .Производная тока через индуктивность 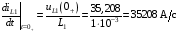 . .3. Составление характеристического уравнения цепи и определение его корней. Составим характеристическое уравнение методом входного сопротивления  В произвольной ветви разорвем цепь и запишем входное сопротивление: 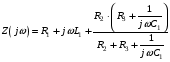 , ,заменив 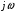 на на 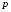 , получим , получим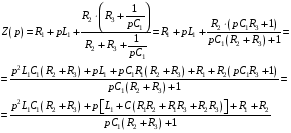 Приравняем 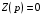 , получим характеристическое уравнение , получим характеристическое уравнение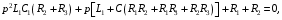 подставим численные значения параметров цепи 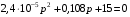 , ,корни характеристического уравнения 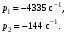 Характеристическое уравнение имеет два действительных и неравных корня, следовательно, переходный процесс в цепи имеет апериодический характер, и свободная составляющая искомой величины имеет вид 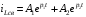 . .Полное решение 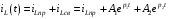 . .4. Расчет принужденного значения.  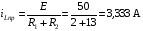 . .5. Определение постоянных интегрирования. 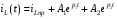 , ,для определения постоянных 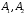 продифференцируем это выражение продифференцируем это выражение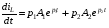 . .При 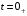 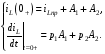 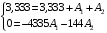 откуда 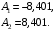 Искомый ток 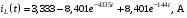 , ,напряжение на индуктивности 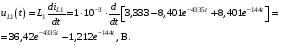 Операторный метод 1. Операторная схема замещения. Учитывая независимые начальные условия, изобразим операторную схему замещения, 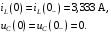  2. Определим ток 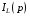 по закону Ома по закону Ома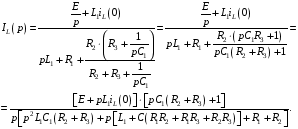 Напряжение на индуктивности 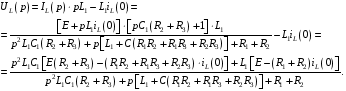 После подстановки числовых значений получим 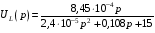 . .3. Определение оригинала искомой величины 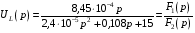 По формуле разложения 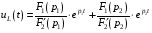 . .Находим корни уравнения 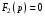 , ,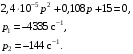 Вычисляем 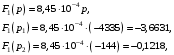 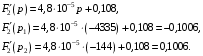 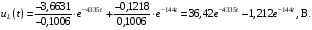 Полученное выражение совпадает с выражением, найденным классическим методом. Построение графиков изменения напряжения Построим график изменения искомой величины в функции времени в интервале от 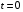 до до 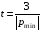 , где , где 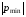 - меньший по модулю корень характеристического - меньший по модулю корень характеристическогоуравнения, 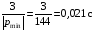 . . |
