Расчётнографическая работа по дисциплине Статистическая радиотехника вариант 1 бригада 5
 Скачать 107.86 Kb. Скачать 107.86 Kb.
|
 МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ФАКУЛЬТЕТ РАДИОТЕХНИКИ И ЭЛЕКТРОНИКИ КАФЕДРА РАДИОПРИЁМНЫХ И РАДИОПЕРЕДАЮЩИХ УСТРОЙСТВ РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА по дисциплине «Статистическая радиотехника» ВАРИАНТ 1 БРИГАДА 5
Новосибирск 2021 год СОДЕРЖАНИЕ Часть 1. Измерение среднего значения…………………………….3 стр. Часть 2. Согласованная фильтрация………………………………..5 стр. Задание 1…………………………………………………………5 стр. Задание 2…………………………………………………………5 стр. Задание 3…………………………………………………………7 стр. Часть 3. Изучение винеровской фильтрации……………………….9 стр. Задание 1…………………………………………………………9 стр. Задание 2…………………………………………………………11 стр. Задание 3…………………………………………………………13 стр. Список использованной литературы………………………………...15 стр.  2 ЧАСТЬ 1. ИЗМЕРЕНИЕ СРЕДНЕГО ЗНАЧЕНИЯ Задание: Отношение 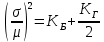 , где , где 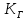 – последняя цифра в номере группы. – последняя цифра в номере группы.Рассчитать длину реализации 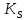 , при которой относительная ошибка , при которой относительная ошибка 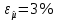 . Округлив значение . Округлив значение 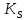 до ближайшего кратного K = 1024, найти соответствующее ему значение до ближайшего кратного K = 1024, найти соответствующее ему значение 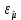 . .Решение: 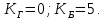 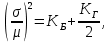 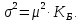 Зададимся математическим ожиданием 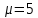 . Тогда: . Тогда: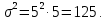 Математическое ожидание: 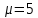 , ,Дисперсия: 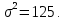 СКО: 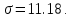 Расчёт длины реализации 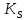 , при которой относительная ошибка равна , при которой относительная ошибка равна 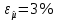 : :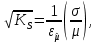 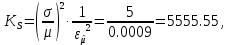 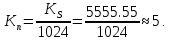 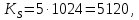  3 Величина относительной ошибки: 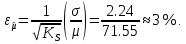 Величина относительной ошибки не превосходит заданную. ВЫВОД: с увеличением объёма выборки 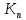 дисперсия уменьшается, т. к. увеличивается точность, что характеризует одно из свойств оценки – её состоятельность. Состоятельная оценка – статистическая оценка параметра распределения вероятностей, обладающая тем свойством, что при увеличении числа наблюдений вероятность отклонения оценки от оцениваемого параметра на величину, превосходящую заданное число, стремится к нулю. дисперсия уменьшается, т. к. увеличивается точность, что характеризует одно из свойств оценки – её состоятельность. Состоятельная оценка – статистическая оценка параметра распределения вероятностей, обладающая тем свойством, что при увеличении числа наблюдений вероятность отклонения оценки от оцениваемого параметра на величину, превосходящую заданное число, стремится к нулю. 4 ЧАСТЬ 2. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ Задание 1: Рассчитать параметры сигнала и шума, при которых полученное на выходе СФ ОСШ 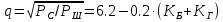 , где , где 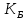 – номер бригады в лабораторном журнале, – номер бригады в лабораторном журнале, 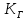 – последняя цифра в номере группы. Длительность сигнала рекомендуется выбирать в пределах – последняя цифра в номере группы. Длительность сигнала рекомендуется выбирать в пределах 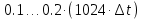 , где , где 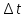 – интервал дискретизации. – интервал дискретизации. Решение: 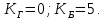 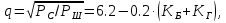 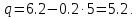 Интервал дискретизации 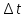 : :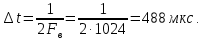 Время наблюдения 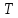 : :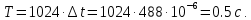 Длительность сигнала 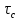 : :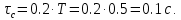 Задание 2: Рассчитать зависимость ОСШ на выходе квазиоптимальных фильтров от постоянной времени интегрирующего звена первого порядка. Найти оптимальные значения параметров, обеспечивающие максимальное ОСШ, и проигрыш по сравнению с СФ. Решение: 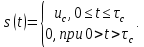  5 Зададимся амплитудой сигнала 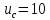 В. В.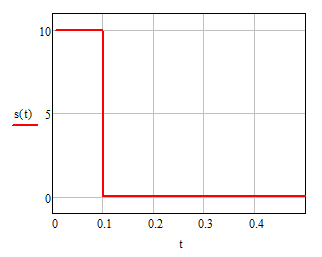 Рис. 2.1. Прямоугольный видеоимпульс Рассчитаем энергию сигнала: 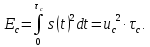 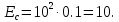 Отношение сигнал/шум на выходе согласованного фильтра: 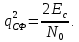 Выражаем и находим уровень шума 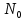 : :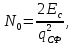  Находим дисперсию шума:   Отношение сигнал/шум на выходе квазиоптимального фильтра (RC):   6 Оптимальное значение постоянной времени интегрирующей RC-цепи: 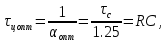 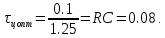 Примем сопротивление 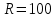 Ом. Тогда ёмкость Ом. Тогда ёмкость 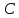 равна: равна: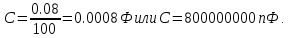 ОСШ на выходе RC-цепи: 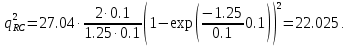 Проверим условие соотношений ОСШ СФ и RC-фильтра: 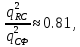 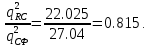 Условие соблюдается. Задание 3: Рассчитайте длину реализации 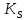 , при которой относительная ошибка измерения дисперсии шума на выходе СФ не превышает 3%. , при которой относительная ошибка измерения дисперсии шума на выходе СФ не превышает 3%.Решение: Длина реализации, при которой относительная ошибка измерения дисперсии шума на выходе СФ не превышает 3%: 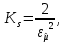 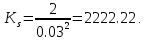 Количество отсчётов 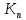 : :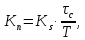 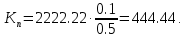 Округлим 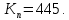  7 ВЫВОД: из расчётов видно, что при использовании квазиоптимального фильтра (фильтра нижних частот) мы несём большие потери в отношении сигнал/шум, по сравнению с согласованным фильтром (20%). Поэтому, нужно увеличивать энергию сигнала (примерно в 1.25), чтобы ОСШ на выходе квазиоптимального фильтра было таким же, как и на выходе согласованного. Таким образом, согласованный фильтр является оптимальным, поскольку обеспечивает минимум отношения сигнал/шум, но из-за того, что согласованный фильтр физически нереализуем (содержит в себе нереализуемый идеальный интегратор и линию задержки), используют квазиоптимальный фильтр с существенно простой реализацией и близкой эффективностью к оптимальному согласованному фильтру.   8 8 ЧАСТЬ 3. ИЗУЧЕНИЕ ВИНЕРОВСКОЙ ФИЛЬТРАЦИИ Задание 1: Рассчитать нормированные дисперсии ошибок фильтрации 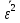 при использовании при использованиифильтра Винера (ФВ); каузального фильтра Винера (КФВ); квазиоптимального фильтра (ФНЧ с прямоугольной АЧХ) при следующих данных: дисперсия сигнала  ; ;интервал корреляции сигнала  спектральная плотность шума  Решение:  Интервал корреляции сигнала: 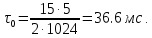 Спектральная плотность шума: 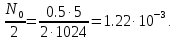 Уровень шума: 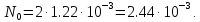 Нормированная дисперсия ошибки при использовании Фильтра Винера определяется как: 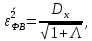  9 где 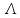 – безразмерный коэффициент, имеющий физический смысл отношения сигнал/шум, который вычисляется по формуле: – безразмерный коэффициент, имеющий физический смысл отношения сигнал/шум, который вычисляется по формуле: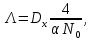 где 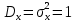 – дисперсия сигнала; – дисперсия сигнала; 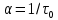 . .Вычислим коэффициент  : :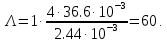 Отсюда нормированная дисперсия ошибки при использовании фильтра Винера: 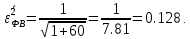 Нормированная дисперсия ошибки при использовании каузального фильтра Винера: 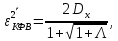  Нормированная дисперсия ошибки при использовании квазиоптимального фильтра Винера:  где  и и  – оптимальные параметры, которые равны: – оптимальные параметры, которые равны:  Подставим эти значения и получим нормированную дисперсию ошибки при использовании квазиоптимального фильтра Винера:    10 Задание 2: Рассчитать зависимости нормированных дисперсий ошибок фильтраций ФВ и КФВ от: а) спектральной плотности шума при заданных в п. 1 значениях  и и  ; ;б) интервала корреляции сигнала при заданных в п.1 значениях  и и  . .Диапазон изменения параметров  в п. 2(а) и в п. 2(а) и  в п. 2(б) должен составлять в п. 2(б) должен составлять  относительно значений, заданных в задании 1. относительно значений, заданных в задании 1.Решение: а) Нормированная дисперсия ошибки фильтрации ФВ:  Нормированная дисперсия ошибки фильтрации КФВ:  где  – СПМ шума в заданном диапазоне изменения – СПМ шума в заданном диапазоне изменения  . . Построим график зависимости нормированных дисперсий ошибок фильтраций ФВ и КФВ от изменения СПМ шума (рис. 3.1).  11  Рис. 3.1. График зависимости нормированных дисперсий ошибок фильтраций ФВ и КФВ от изменения СПМ шума б) Нормированная дисперсия ошибки фильтрации ФВ:  Нормированная дисперсия ошибки фильтрации КФВ:  где  – интервал корреляции сигнала в заданном диапазоне изменения – интервал корреляции сигнала в заданном диапазоне изменения  . . Построим график зависимости нормированных дисперсий ошибок фильтраций ФВ и КФВ от изменения интервала корреляции сигнала (рис. 3.2).  12  Рис. 3.2. График зависимости нормированных дисперсий ошибок фильтраций ФВ и КФВ от изменения интервала корреляции Задание 3: Рассчитать объём выборки (количество  независимых реализаций), при которой относительная ошибка измерения в эксперименте величины независимых реализаций), при которой относительная ошибка измерения в эксперименте величины  не превысит 1%. При этом приближённо принять интервал корреляции не превысит 1%. При этом приближённо принять интервал корреляции  текущей ошибки фильтрации текущей ошибки фильтрации  равным удвоенному интервалу корреляции равным удвоенному интервалу корреляции  процесса процесса 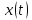 , а отсчёты, отстоящие на интервал корреляции – независимыми. , а отсчёты, отстоящие на интервал корреляции – независимыми. Решение: Интервал дискретизации: 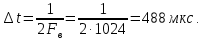 Интервал корреляции, согласно заданию, определяется как: 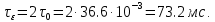  13 Длина реализации, при котором относительная ошибка измерения в эксперименте величины 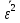 не превысит 1%: не превысит 1%: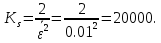 Количество отсчётов 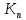 : :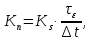 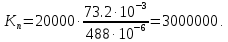 Объём выборки: 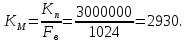 ВЫВОД: из расчётов видно, что лучшие результаты искомых параметров показывает некаузальный фильтр Винера (ФВ), так как он обеспечивает минимум нормированной дисперсии ошибки, по сравнению с квазиоптимальным и каузальным фильтрами. Но фильтр Винера физически нереализуем, что является его существенным недостатком. Это связано с тем, что некаузальный ФВ, использует все входные данные для получения оценки - от ранее поступивших до будущих. Использование прошлых данных, т. е. уже поступивших к текущему моменту времени, физически оправдано и технически реализуемо, а использование будущих данных - невозможно. Каузальный фильтр Винера, физически реализуем и формирует оценку только за счёт ранее поступивших данных, но имеет ошибку фильтрации значительно выше, чем квазиоптимальный фильтр и фильтр Винера. Это связано с тем, что для образования оценки он использует малое количество данных, в отличие от НКФВ и КОФВ.   14 14 СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ Применение теории случайных процессов: уч. пособие/ И. С. Грузман. – Новосибирск: Изд-во НГТУ, 2006. – 84 с.; Основы случайных процессов: уч. пособие/ И. С. Грузман. – Новосибирск: Изд-во НГТУ, 2004. – 96 с.; Лабораторный практикум по курсу “статистическая радиотехника”. Методические указания к лабораторным работам № 1-3 для студентов факультета радиотехники, электроники и физики (специальности 2007) всех форм обучения: уч. пособие/ А. А. Спектор, И. С. Грузман. – Новосибирск: Изд-во НГТУ, 1998. – 33 с.   15 15 |
