Расчетно графическая работа по финансовой математике. Расчетнографическая работа по финансовой математике
 Скачать 170.33 Kb. Скачать 170.33 Kb.
|
|
КАЗАНСКИЙ ИННОВАЦИОННЫЙ УНИВЕРСИТЕТ ИМ. В. Г. ТИМИРЯСОВА (ИЭУП) РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА ПО ФИНАНСОВОЙ МАТЕМАТИКЕ Вариант 58 Выполнил: студент группы № 101c Мухамедшин Айдил Ринатович Зачетная книжка № 20-1-58 Преподаватель: Гафиятова О.В. Казань – 2022г. Задание 1Денежные средства в размере 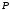 рублей размещаются в виде рублевого депозита, на который начисляются простые проценты по ставке рублей размещаются в виде рублевого депозита, на который начисляются простые проценты по ставке 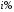 . .Дата 1 – дата начала операции, Дата 2 – дата конца операции. Определить начисляемые проценты и наращенные суммы при начислении по британскому, французскому и германскому методу для двух случаев: если депозит будет открыт и закрыт в 2020 году; если депозит будет открыт и закрыт в 2021 году. Основные результаты решения оформить в виде таблицы:
P = (8+5+5) * 50000 = 900000; i = 0,5 * (8+5) + 4 = 10,5% Дата 1 - 23 января Дата 2 – 16 июля Решение: 2020 год T = 366 2021 год T = 365 Точное кол-во дней t = 174 t = 173 Приближенное: t = 173 t = 173 Наращенная сумма 2020 год: 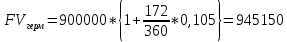 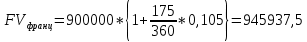 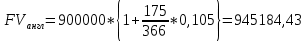 Начислямые проценты 2020г: (PV-FV) Британский метод – 900000 - 945184,43 = 45184,43 Французский – 900000 – 945937,5 = 45937,5 Германский – 900000 – 945412,5 = 45412,5 Наращенная сумма 2021 год: 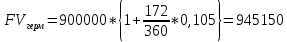 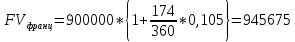 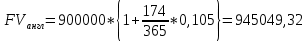 Начислямые проценты 2021г: (PV-FV) Британский метод – 900000 – 945049,32 = 45049,32 Французский – 900000 – 945675 = 45675 Германский – 900000 – 945150 = 45150 Задание 2Денежные средства в размере 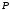 рублей размещаются в виде рублевого депозита на один год с ежемесячным начислением процентов с капитализацией. Номинальная годовая ставка начисления процентов равна рублей размещаются в виде рублевого депозита на один год с ежемесячным начислением процентов с капитализацией. Номинальная годовая ставка начисления процентов равна 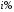 . Дата начала операции – Дата 1, год 2021. . Дата начала операции – Дата 1, год 2021.Операция прерывается раньше срока. Дата прерывания операции – Дата 2, год 2021. Определить начисляемые проценты и наращенные суммы, если, согласно договору, при досрочном расторжении должна быть применена схема: дробного процента; смешанного процента; без начисления процентов за неполный последний период начисления. При расчетах неполного месяца считать, что в полном месяце30 дней. Основные результаты решения оформить в виде таблицы:
Решение: P = (8+5+5) * 50000 = 900000; i = 0,5 * (8+5) + 4 = 10,5% Дата 1 - 23 января 2021 г. Дата 2 – 16 июля 2021 г. Полных месяцев N = 5 i = 0,105/12 = 0,00875 – ежемесячное начисление процентов 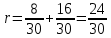 ; ;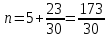 ; ;1)Наращенная сумма по дробной схеме начисления процентов: 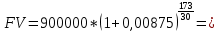 946370,01 946370,012) Смешанный метод: 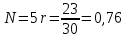 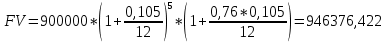 3) без начисления процентов за неполный последний период начисления 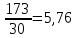 – 5 полных месяцев, оставшиеся 23 дня не учитываются – 5 полных месяцев, оставшиеся 23 дня не учитываются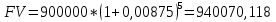 Задание 3У банка имеется возможность кратковременного размещения средств по двум схемам: СХЕМА 1 – выдать денежные средства в размере 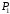 рублей на рублей на 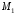 месяцев и получить в конце операции месяцев и получить в конце операции 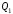 рублей; рублей;СХЕМА 2 – выдать денежные средства в размере 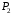 рублей на рублей на 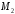 месяцев и получить в конце операции месяцев и получить в конце операции 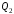 рублей. рублей.Определить, какая из схем наиболее выгодна для банка, если операции оцениваются по правилу простого процента. Вывод обосновать. Данные для расчетов в задании 3: 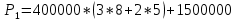 ; ; 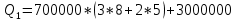 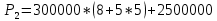 ; ; 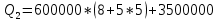 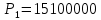 ; ; 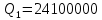 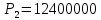 ; ; 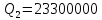 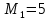 ; ; 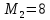 Схема 1: 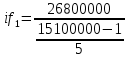 =0,15496=15,496% =0,15496=15,496%Схема 2: 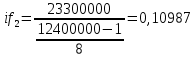 =10,987% =10,987%Для банка более выгодной схемой является с наибольшей процентной ставкой в месяц. Эффективная ставка Схемы 1 – 15,49 % в месяц, а для Схемы 2 – 10,98 % в месяц. Для банка наиболее выгодна СХЕМА 1, так как ее процентная ставка выше СХЕМЫ 2 на 1%. Годовые процентные ставки: Схемы 1: 12 * 0,15496 = 1,85952 = 185,95% в год Схемы 2: 12 * 0,10987 = 1,31844 = 131,84% Задание 4В банк сделан вклад в размере 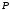 рублей сроком на рублей сроком на 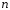 лет под лет под 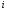 % годовых. Проценты начисляются по схеме сложного процента. % годовых. Проценты начисляются по схеме сложного процента.Определить, какая сумма будет возвращена в конце срока операции, если проценты начисляются и капитализируются: а) раз в год; б) раз в полгода; в) раз в квартал; г) раз в два месяца; д) раз в месяц; е) два раза в месяц; ж) раз в неделю (считать, что в году ровно 53 недели); з) раз в день (считать, что в году 365 дней); и) непрерывно. Для всех указанных случаев определить эффективную годовую процентную ставку (в этом задании – с точностью до тысячной доли процента). Построить график зависимости эффективной процентной ставки от числа начислений процентов в год. Основные результаты решения оформить в виде таблицы:
Данные для расчетов в задании 4: P = (8 + 5 + 5) * 50000 = 900000; i = 0,5 * (8 + 5) + 4 =10,5 ; n = 5 + 4 = 9 Решение а) раз в год m = 1 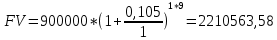 б) раз в пол года m = 2 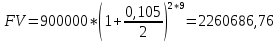 в) раз в квартал m = 4 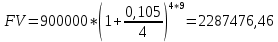 г) раз в два месяца m = 6 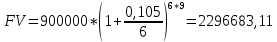 д) раз в месяц m = 12 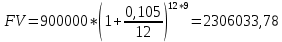 е) два раза в месяц m = 24 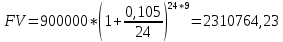 ж) раз в неделю m = 53 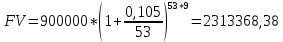 з) раз в день m = 365 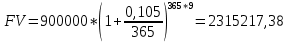 и) непрерывно; число Эйлера = 2,718281828 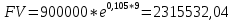 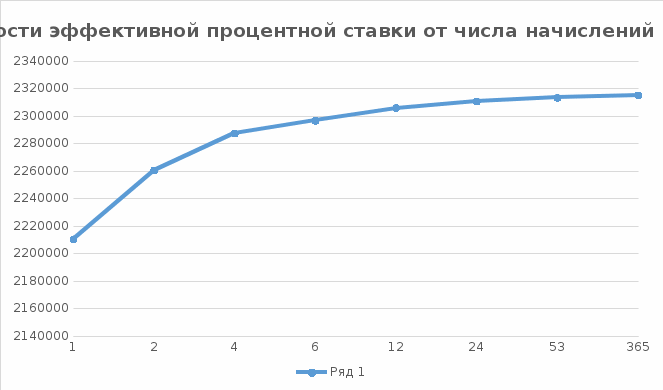 Эффективная процентная ставка а) 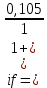 б) 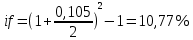 в)  г) 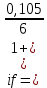 д) 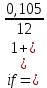 е) 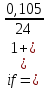 ж) 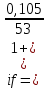 з) 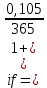 и) 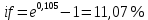 Задание 5В банк сделан вклад в размере 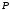 рублей сроком на рублей сроком на 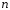 лет под лет под 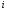 % годовых. Проценты начисляются по схеме сложного процента. Проценты начисляются так, как указано в таблице с данными к заданию. % годовых. Проценты начисляются по схеме сложного процента. Проценты начисляются так, как указано в таблице с данными к заданию.За указанный период времени среднегодовой уровень инфляции составил 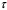 %. %.Определить: реальную наращенную сумму за указанный период времени; реальную годовую процентную ставку; компенсирующую годовую процентную ставку указанной операции, соответствующую данному уровню инфляции; обеспечивающую годовую процентную ставку указанной операции, для реальной доходности 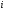 % в год при данном уровне инфляции. % в год при данном уровне инфляции.Основные результаты решения оформить в виде таблицы:
Данные для расчетов в задании 5: P = (8 + 5 + 5) * 50000 = 900000; i = 0,5 * (8 + 5) + 4 =10,5 ; n = 5 + 4 = 9 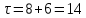 Период начисления процентов два раза в месяц m = 24 Решение 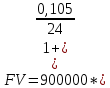 1)Реальная наращенная сумма 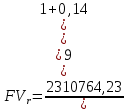 2)Реальная годовая процентная ставка 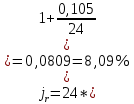 3) компенсирующая годовая ставка 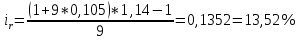 4) обеспечивающая годовая процентная ставка 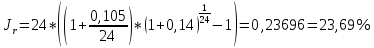 Задание 6У предпринимателя есть ценная бумага, гарантирующая выплату по ней в размере 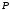 рублей через рублей через 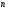 лет. Предприниматель, желая получить деньги прямо сейчас, переуступает это обязательство банку. Банк согласен принять данную ценную бумагу с дисконтом лет. Предприниматель, желая получить деньги прямо сейчас, переуступает это обязательство банку. Банк согласен принять данную ценную бумагу с дисконтом 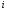 % годовых. % годовых.Определить, какая сумма будет выплачена предпринимателю, если дисконтирование будет осуществлено по следующим схемам: а) по правилу математического дисконтирования с простым процентом; б) по правилу математического дисконтирования со сложным процентом; в) по правилу банковского учета с простым процентом; г) по правилу банковского учета со сложным процентом. Для вариантов, в которых получатся отрицательные значения, прокомментировать их. Основные результаты решения оформить в виде таблицы:
Данные для расчетов в задании 6 P = (8 + 5 + 5) * 50000 = 900000; i = 0,1 * (8 + 5) + 4 = 5,3; n = 5 + 4 = 9 Решение а) по правилу математического дисконтирования с простым процентом; 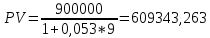 б) по правилу математического дисконтирования со сложным процентом; 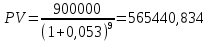 в) по правилу банковского учета с простым процентом; 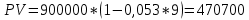 г) по правилу банковского учета со сложным процентом 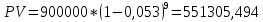 Задание 7У финансовой организации есть три варианта долгосрочного вложения средств: ВАРИАНТ 1 – вложить денежные средства в размере 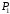 руб. на руб. на 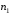 лет в банк под лет в банк под 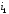 % годовых с ежеквартальным начислением процентов; % годовых с ежеквартальным начислением процентов;ВАРИАНТ 2 – вложить средства в размере 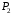 руб. на руб. на 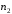 лет в проект, который принесет в конце срока не облагаемый налогом доход лет в проект, который принесет в конце срока не облагаемый налогом доход 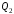 рублей; рублей;ВАРИАНТ 3 – вложить денежные средства в размере 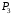 рублей на рублей на 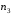 лет в бизнес, который принесет в конце срока доход лет в бизнес, который принесет в конце срока доход 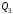 рублей, но нужно будет заплатить налог рублей, но нужно будет заплатить налог 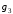 % со всего полученного дохода. % со всего полученного дохода.Определить, какой из вариантов вложения средств наиболее выгоден для финансовой организации, если операции оцениваются по правилу сложного процента. Вывод обосновать. Данные для расчетов в задании 7: P1 = (8 + 5 + 5) * 50000 = 900000; i = 0,5 * (8+5) + 4 = 10,5; n1 = 5 + 4 = 9; P2 = (2 * 5 + 4) * 40000 = 560000; Q2 = (3 * 5 + 4) * 60000 = 1140000; n2 = 6 + 5 = 11; P3 = (50 – 5 * 8) * 20000 = 200000; Q3 = (50 – 4 * 8) * 30000 = 540000; n3 = 4 + 8 = 12 g3 = 0,5 * 8 + 5 = 9 ВАРИАНТ 1 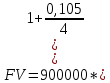 =2287476,46 =2287476,46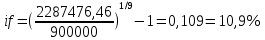 ВАРИАНТ 2 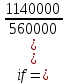 ВАРИАНТ 3 Сумма после уплаты налога = 491400 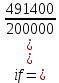 чем выше эффективная ставка финансовой операции, тем она выгоднее для вкладчика, в данном случае это вариант 1 Задание 8Государство Y просит в долг у государства X денежную сумму в размере 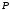 млрд. €. По взаимной договоренности установлена процентная ставка кредитной операции в размере млрд. €. По взаимной договоренности установлена процентная ставка кредитной операции в размере 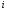 %. Согласно договору займа, долг должен быть возвращен двумя платежами: %. Согласно договору займа, долг должен быть возвращен двумя платежами: 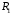 млрд. € через млрд. € через 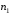 лет и лет и 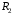 млрд. € через млрд. € через 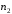 лет. лет.Определить, какой должна быть сумма второго платежа 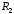 , при известной сумме первого платежа , при известной сумме первого платежа 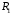 млрд. €. млрд. €.Первый платеж выполнен вовремя в полном объеме. Но к моменту второго платежа 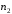 в государстве Y разразился экономический кризис, и оно настаивает на реструктуризации выплат. На переговорах государство-заемщик Y предлагает государству-кредитору X два варианта реструктуризации: в государстве Y разразился экономический кризис, и оно настаивает на реструктуризации выплат. На переговорах государство-заемщик Y предлагает государству-кредитору X два варианта реструктуризации:ВАРИАНТ 1. Единым платежом в размере 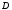 млрд. € с переносом его на момент времени млрд. € с переносом его на момент времени 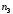 лет от даты взятия в долг. лет от даты взятия в долг.ВАРИАНТ 2. Двумя равными платежами в размере 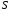 млрд. €, один в указанный в договоре момент времени млрд. €, один в указанный в договоре момент времени 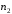 лет от даты взятия в долг, а второй в момент времени лет от даты взятия в долг, а второй в момент времени 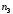 лет от даты взятия в долг. лет от даты взятия в долг.Государство-кредитор X вынуждено согласиться с каким-либо вариантом, иначе оно рискует не получить деньги вовсе. Определить, какой из двух перечисленных вариантов будет выбран государством-кредитором X? Изменилась ли его выгода от предоставленного кредита относительно исходных условий договора и в какую сторону? Данные для расчетов в задании 8 P = 44; 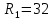 ; D = 18; S = 10; i = 5,5; ; D = 18; S = 10; i = 5,5; 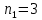 ; ; 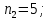 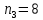 Решение Сумма второго платежа 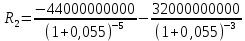 ≈ -19930519000 € ≈ -19930519000 €ВАРИАНТ 1 Единым платежом 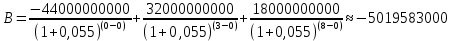 Как видно из баланса, этот вариант не выгоден государству кредитору так как баланс оказался отрицательным. ВАРИАНТ 2. Двумя равными платежами 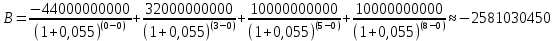 Вывод: 1) Сумма второго платежа по договору займа должна быть равна 19930519000 2) Государством кредитором будет выбран 1 Вариант реструктуризации так как -5019583000 > -2581030450 3)Второй вариант реструктуризации выгоднее для государства-заемщика потому что чистая приведенная стоимость по второму варианту чем по первому варианту. Не до конца Задание 9Инвестор рассматривает вариант покупки торгового комплекса за 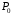 млн. руб. Перестройка комплекса потребует вложения через год еще млн. руб. Перестройка комплекса потребует вложения через год еще 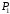 млн. руб. Оборудование комплекса обойдется в млн. руб. Оборудование комплекса обойдется в 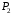 млн. руб. и эти затраты будут произведены через 2 года. Прибыль от комплекса ожидается в размере млн. руб. и эти затраты будут произведены через 2 года. Прибыль от комплекса ожидается в размере 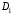 млн. руб. через млн. руб. через 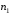 лет, лет, 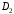 млн. руб. через млн. руб. через 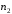 лет и лет и 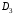 через через 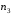 лет. В конце лет. В конце 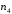 года комплекс планируется продать за года комплекс планируется продать за 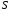 млн. руб. В остальные годы доходы и расходы практически компенсируют друг друга. млн. руб. В остальные годы доходы и расходы практически компенсируют друг друга.1. Определить (только на основе понятия чистого приведенного дохода NPV): а) выгоден ли для инвестора предлагаемый проект, если он ожидает от вложения нормы доходности не ниже чем 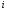 % годовых? % годовых?б) останется ли проект выгодным, если ожидания инвестора станут равными 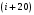 % годовых? % годовых?2. Определить с использованием функции ВСД MS Excel внутреннюю норму доходности (IRR) проекта. Ответить на пункты (а) и (б) вопроса 1 на основе понятия внутренней норы доходности. 3. Определить срок окупаемости проекта для случая (а), понимая подданным понятием год, когда проект даст первый положительный накопленный чистый приведенный доход.
Данные для расчета в задании 9: 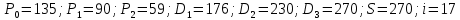 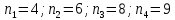 Решение В момент покупки n1 = 0, а доход от инвестиции D1 = 0 Вложения через год n2 = 1, расходы P1 = 90, доход D2 = 0 Через два года n3 = 2, расходы P2 = 59, доход D3 = 0 Через четыре года n4 = 4, расходов нет, доход D4 = 176 млн.руб Через шесть лет n5 = 6, расходов нет, доход D5 = 230 млн.руб Через восемь лет n6 = 8, расходов нет, доход D6 =270 млн.руб Через девять лет n7 = 9, расходов нет, доход от продажи = 270 млн.руб 1) А) NPV при ставке 17% 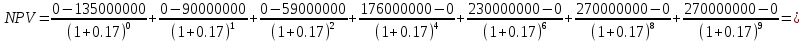 71172158,51 71172158,51NPV>0 проект можно признать выгодным при годовой норме доходности 17% Б) NPV при ставке 37% 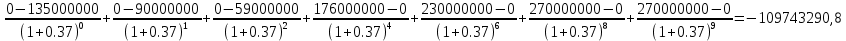 NPV<0 проект следует признать невыгодным при годовой норме доходности 37% Определить с использованием функции ВСД MS Excel внутреннюю норму доходности (IRR) проекта.
Годовая внутренняя норма доходности операции по покупке торгового комплекса равна 22% в год. Значит, если инвестор рассчитывает на доходность 17%, то покупка торгового комплекса выгодна, так как 22% > 17%. Если же инвестор рассчитывает на доходность 37%, то покупка не выгодна, так как внутренняя норма доходности IRR равна 22%, а это меньше на 15% ожидаемой доходности. 3. Определить срок окупаемости проекта для случая (а), понимая подданным понятием год, когда проект даст первый положительный накопленный чистый приведенный доход. 1) 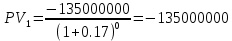 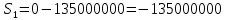 2) 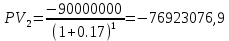 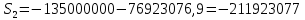 3) 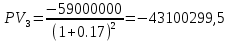 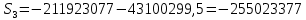 4) 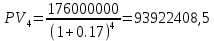 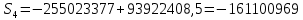 5) 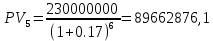 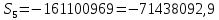 6) 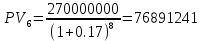 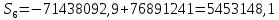 Положительный результат достигнут на 6 шаге, тогда период окупаемости равен 8 лет Задание 10 (задание повышенного уровня)Банк предлагает предпринимателю кредит в размере 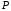 рублей с номинальной годовой процентной ставкой рублей с номинальной годовой процентной ставкой  %. Проценты начисляются ежемесячно. Рассматриваются различные варианты срока кредита – 5, 6, 7, 8, 9 и 10 лет. Интервалы выплат – раз в месяц. %. Проценты начисляются ежемесячно. Рассматриваются различные варианты срока кредита – 5, 6, 7, 8, 9 и 10 лет. Интервалы выплат – раз в месяц.Возврат кредита осуществляется аннуитетным способом (общие выплаты равными платежами). Определить размер ежемесячного платежа для каждого варианта срока кредита. Построить графики общей суммы возврата и ежемесячного платежа в зависимости от срока кредита. Сделать вывод о выгодности для предпринимателя того или иного варианта получения кредита в зависимости от экономической ситуации. Какие еще выводы можно сделать на основе решения этого задания? Данные для расчетов в задании 10: 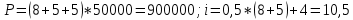 Аннуитетный платеж 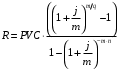 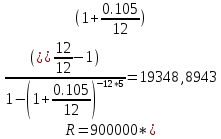 Определим выплаты процентов и основной части долга. 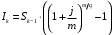 ; ;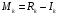 ; ;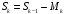 ; ;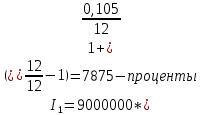 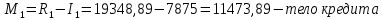 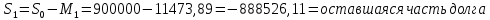 Общее количество выплат: 19348,89 * 60 (кол-во месяцев) = 1160933,4 Проценты по кредиту: 1160933,4-900000 = 260933,4 Расчеты по остальным периодам проводились в программе MSExcel: 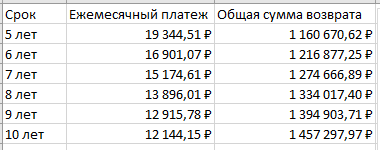 Таблица 1. Расчеты по кредиту с процентной ставкой 10,5% 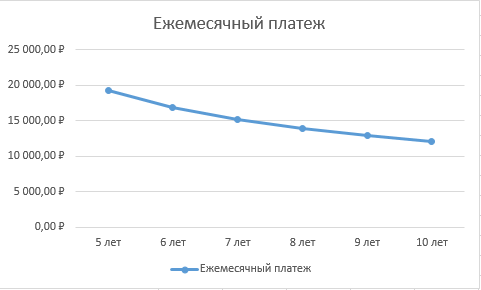 График ежемесячных выплат в зависимости от срока 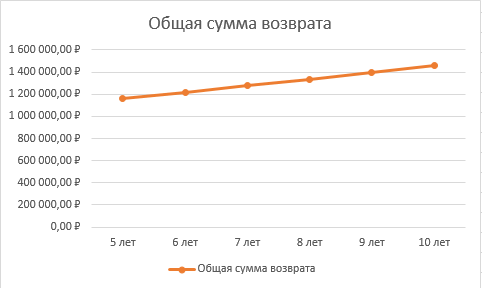 График общей суммы выплат с процентами Выводы: По результатам расчетов мы можем наблюдать следующие варианты кредитования представленные банком для предпринимателя (Таблица 1). При выборе плана с наиболее меньшим сроком (5 лет) переплата будет ниже но при этом ежемесячные выплаты будут гораздо выше чем при длительном сроке (10 лет) на 60%. А при кредитовании с более длительным сроком, ежемесячные выплаты будут ниже но общая сумма возврата с процентами будет выше на 25% чем при кредите на 5 лет. |