РГР Фин.математика. РГР (1). Расчетнографическая работа по финансовой математике
 Скачать 104.92 Kb.
|
 КАЗАНСКИЙ ИННОВАЦИОННЫЙ УНИВЕРСИТЕТ ИМ. В. Г. ТИМИРЯСОВА (ИЭУП)РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА ПО ФИНАНСОВОЙ МАТЕМАТИКЕ Вариант 21 Выполнил: студент группы № 102у Имамова Регина Робертовна зачетная книжка № 10021-з Преподаватель: (проф.; доц.; ст. преп.) Шевченко Д.В. Набережные Челны – 2021 г. Содержание В  ведение………………………………………………………………………………….3Задание 1……………………………………………………………………………...…..4 Задание 2…………………………………………………………………………….……7 Задание 3……………………………………………………………………………...…10 Задание 4…………………………………………………………………………...……12 Задание 5………………………………………………………………………...………16 Задание 6……………………………………………………………………………..….18 Задание 7……………………………………………………………………………..….20 Задание 8…………………………………………………………………………...……23 Заключение………………………………………………………………………...……26 Список использованной литературы…………………...………………………..……28 Введение В работе были использованы основные необходимые формулы такие как: Формула для нахождения наращенных сумм: по германской практике: 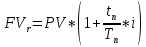 по французской практике: 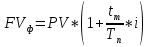 по британской практике: 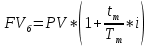 Формула для нахождения наращенной суммы по дробной схеме начисления процентов: 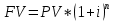 Формула для нахождения наращенной суммы по схеме начисления смешанного процента:  Формула для нахождения наращенной суммы по схеме без начисления процентов за неполный последний период начисления: 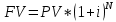 Формула для нахождения реальной процентной ставки: 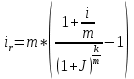 Формула для нахождения компенсирующей ставки: 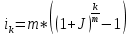 Формула для нахождения обеспечивающей ставки: 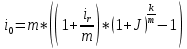 Общую формула для определения эффективной годовой процентной ставки:  Задание 1 Денежные средства в размере P рублей размещаются в виде рублевого депозита, на который начисляются простые проценты по ставке i%. Дата 1 – дата начала операции, Дата 2 – дата конца операции. Определить начисляемые проценты и наращенные суммы при начислении по британскому, французскому и германскому методу для двух случаев: 1) если депозит будет открыт и закрыт в 2020 году; 2) если депозит будет открыт и закрыт в 2021 году. Данные для расчетов в заданиях 1 и 2: a = 1; b = 2; Р = (a + b + 5) * 50000 = (1 + 2 +5) * 50000 = 400000; i 0,5 * a b 4 = 0,5 * (1 + 2) + 4 =5,5.
Дата 1: число 12 + 6 = 18 , месяц – февраль, т.е. 18 февраля; Дата 2: число 27 – 6 = 21 , месяц – октябрь, т.е. 21 октября. Решение: если депозит будет открыт и закрыт в 2020 году. Определим точное и приближенное число дней указанной операции. Точное число дней в високосной год: 17 дней в феврале (от 13 до 29); 31 день в марте; 30 дней в апреле;31 день в мае; 30 дней в июне; 31 день в июле; 31 день в августе; 30 дней в сентябре; 26 дней в октябре (от 1 до 26). Из общего количества дней необходимо вычесть 1, так как день открытия и закрытия операции считаются одним днем. В итоге получаем точное число дней: 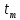 17+31+30+31+30+31+31+30+26-1=256.Приближенное число дней: 17 дней в феврале (от 13 до 29); По 30 дней в семи месяцах: в марте; апреле; мае; июне; июле; августе; сентябре; 26 дней в октябре (от 1 до 26). Из общего количества дней необходимо вычесть 1, так как день открытия и закрытия операции считаются одним днем. Получаем приближенное число дней: 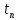 17+30*7+26-1=252Так как 2020 год високосный, то точное число дней в году равно  366 . Приближенное число дней в любом году равно  360. Таким образом, наращенные суммы будут равны: по германской практике: 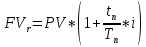=  по французской практике: 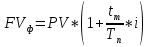= по британской практике: 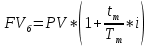= 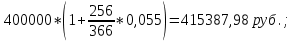2) если депозит будет открыт и закрыт в 2021 году; (Не високосный год) Так как 2021 год не високосный, то точное число дней в году равно 365 Приближенное число дней в любом году равно 360. Таким образом, наращенные суммы будут равны: по германской практике: 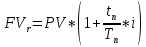=  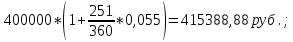по французской практике: 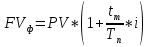= 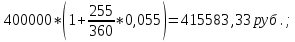по британской практике: 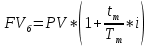=  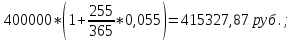Основные результаты решения Задания 1
Отличительной чертой расчета високосного и не високосного года является еще один день расчета (28 и 29 дней в году), за счет чего и происходит понижение выплат в 2021 году в сравнении с 2020 годом. Следует отметить, что наиболее выгодным из всех методов является французский, это связано с тем, что к расчету принимается точное количество дней начислений на приблизительное число дней в году. Задание 2 Денежные средства в размере P рублей размещаются в виде рублевого депозита на один год с ежемесячным начислением процентов с капитализацией. Номинальная годовая ставка начисления процентов равна i%. Дата начала операции – Дата 1, год 2021. Операция прерывается раньше срока. Дата прерывания операции – Дата 2, год 2021. Определить начисляемые проценты и наращенные суммы, если, согласно договору, при досрочном расторжении должна быть применена схема: 1) дробного процента; 2) смешанного процента; 3) без начисления процентов за неполный последний период начисления. При расчетах неполного месяца считать, что в полном месяце30 дней. Данные для расчетов в задании 2: такие же, как и для задания 1.
Решение: 1) Определим полное число месяцев между датами финансовой операции. С 13.02.2021 по 26.10.2021 всего 8 полных месяцев. Значит N 8. Определим дробную часть периода. С 13.10.2021 по 26.10.2021 будет 14 - 1=13 дней. Значит дробная часть 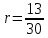 .Таким образом, 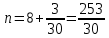 .Так как процентная ставка уже соответствует периоду начисления, никаких преобразований для нее делать не нужно. Наращенная сумма по дробной схеме начисления процентов:   415727,092Процент, будет равен: I = FV - PV 415727,092 – 400000 = 15727,092 руб. 2) Определим полное число месяцев между датами финансовой операции. С 13.02.2021 по 26.10.2021 всего 8 полных месяцев. Значит N = 8. Определим оставшийся неполный интервал времени. Для этого сначала найдем число дней между 13.10.2021 по 26.10.2021 будет 14 - 1= 13 дней. Значит, 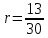.Заметим, что начисления процентов происходят помесячно, а в договоре зафиксирована годовая процентная ставка j = 5,5% = 0,055. Тогда ставка, отнесенная к расчетному периоду времени (ежемесячному) будет равна 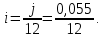 Так как в году 12 месяцев. Наращенная сумма по формуле смешанного процента будет равна: =  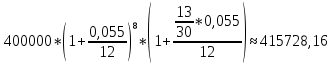Процент, будет равен: I = FV - PV =415728,16 – 400000 = 15728,16 3) Определим полное число месяцев между датами финансовой операции. С 13.02.2021 по 26.10.2021 всего 8 полных месяцев. Значит N = 8. Заметим, что начисления процентов происходят помесячно, а в договоре зафиксирована годовая процентная ставка j = 5,5% = 0,055. Тогда ставка, отнесенная к расчетному периоду времени (ежемесячному) будет равна 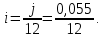Наращенная сумма по схеме без начисления процентов за неполный последний период начисления будет равна: 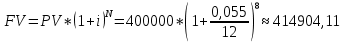 Процент, будет равен: I = FV – PV = 414904,11 – 400000 = 14904,11 Основные результаты решения Задания 2
Вывод: на основе данных таблицы видно, что схема дробного процента является самым высоким процентом начисления и наращивания суммы. Задание 3 У банка имеется возможность кратковременного размещения средств по двум схемам: СХЕМА 1 – выдать денежные средства в размере P1 рублей на M1 месяцев и получить в конце операции Q1 рублей; СХЕМА 2 – выдать денежные средства в размере P2 рублей на M2 месяцев и получить в конце операции Q2 рублей. Определить, какая из схем наиболее выгодна для банка, если операции оцениваются по правилу простого процента. Вывод обосновать.
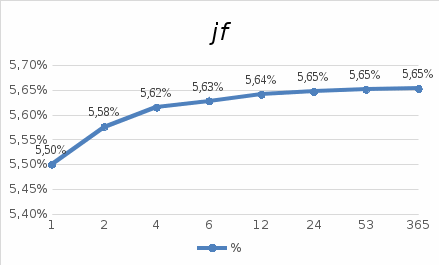
Данные для расчетов в задании 3: P1 4000003 a 2 b1500000=400000*(3*1+2*2)+1500000=4300000; Q1 7000003 a 2b 3000000=700000*(3*1+2*2)+3000000=7900000; M1 4; P2 300000a 5b 2500000=300000*(1+5*2)+2500000=5800000; Q2 600000a 5b 3500000=600000*(1+5*2)+3500000=10100000; M2 10. Решение: Первая схема:  20,93%Вторая схема:  Вывод: Для банка наиболее выгодной является схема с наибольшей процентной ставкой. Значит он выберет для кратковременного размещения средств первую схему со ставкой 20,93%. Для более наглядного сравнения можно привести обе ставки к годовым: 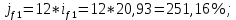 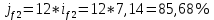 .Задание 4 В банк сделан вклад в размере P рублей сроком на n лет под i % годовых. Проценты начисляются по схеме сложного процента. Определить, какая сумма будет возвращена в конце срока операции, если проценты начисляются и капитализируются: а) раз в год; б) раз в полгода; в) раз в квартал; г) раз в два месяца; д) раз в месяц; е) два раза в месяц; ж) раз в неделю (считать, что в году ровно 53 недели); з) раз в день (считать, что в году 365 дней); и) непрерывно. Для всех указанных случаев определить эффективную годовую процентную ставку (в этом задании – с точностью до тысячной доли процента). Построить график зависимости эффективной процентной ставки от числа начислений процентов в год. (Рекомендуется использовать логарифмическую шкалу для оси отображения числа начислений процентов в год. Непрерывное начисление на график не заносить). Данные для расчетов в задании 4: P a b 550000=(1+2+5)*50000=400000; i 0,5a b 4=0,5*(1+2)+4=5,5; n b 4=2+4=6. Решение: Во всех указанных случаях для расчета наращенной суммы необходимо использовать правило сложного процента. В случаях 1) – 8) используется формула: 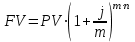 PV=400000 рублей; j=5,5=0,055; n=6. Число m зависит от схемы наращения: 1) проценты начисляются и капитализируются раз в год, тогда m=1  551537,12 руб.2) проценты начисляются и капитализируются раз в полгода, тогда m=2 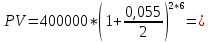 553913,51 руб.3) проценты начисляются и капитализируются раз в квартал, тогда m=4  555137,81 руб.4) проценты начисляются и капитализируются раз в два месяца, тогда m=6 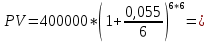 555551,45 руб.5) проценты начисляются и капитализируются раз в месяц, тогда m=12  555967,92 руб.6) проценты начисляются и капитализируются два раза в месяц, тогда m=24 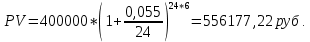 7) проценты начисляются и капитализируются раз в неделю (считать, что в году ровно 53 недели), тогда m=53  8) проценты начисляются и капитализируются раз в день (считать, что в году 365 дней), тогда m=365  556373,42 руб.9) используется формула для непрерывного наращения процентов:  556387,25 руб.Построим график наращенной суммы в зависимости от числа наращений в год (без учета последнего случая). Для этого сначала составим таблицу:
 Для примера использования формулу расчетов эффективных процентных ставок, рассчитаем случаи 1) – 4) по общей формуле, а случаи 5) – 9) – по частным.   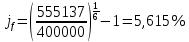 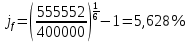  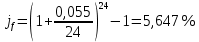 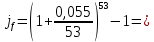 5,651%  5,654%Построим график наращенной суммы в зависимости от числа наращений в год (без учета последнего случая). Для этого сначала составим таблицу:
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
