РГР Фин.математика. РГР (1). Расчетнографическая работа по финансовой математике
 Скачать 104.92 Kb. Скачать 104.92 Kb.
|
|
Основные результаты решения Задания 4
Задание 5 В банк сделан вклад в размере P рублей сроком на n лет под i % годовых. Проценты начисляются по схеме сложного процента. Проценты начисляются так, как указано в таблице с данными к заданию. За указанный период времени среднегодовой уровень инфляции составил j %. Определить: 1) реальную наращенную сумму за указанный период времени; 2) реальную годовую процентную ставку; 3) компенсирующую годовую процентную ставку указанной операции, соответствующую данному уровню инфляции; 4) обеспечивающую годовую процентную ставку указанной операции, для реальной доходности i % в год при данном уровне инфляции. Данные для расчетов в задании 5: P=(a+b+5)*50000=(1+2+5)*50000=400000 i=0,5*(a+b)+4=0,5*(1+2)+4=5,5 n=b+4=2+4=6 j=a+6=1+6=7 проценты начисляются раз в два месяца Решение: 1) Реально наращенная сумма Определим сначала сумму, которую получит вкладчик в конце вклада. Так как проценты начисляются раз в два месяца, то есть 6 раза в год, то m=6. Число лет n=6: 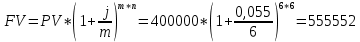 руб. руб.Определим реальную наращенную сумму. Так как уровень инфляции отнесен к году, то k=1. Реальная наращенная сумма будет равна: 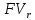 = =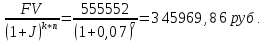 В данном случае за счет высокой инфляции вкладчик получит сумму, позволяющую приобрести товаров в среднем меньше, чем это можно было сделать до вклада. 2) Определим по формуле реальную процентную ставку 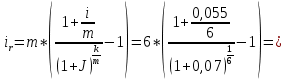 -0,34=-3,4% -0,34=-3,4%3) По формуле определяем компенсирующую ставку: 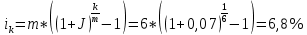 То есть для того, чтобы данная банковская операция компенсировала инфляционный рост цен, необходимо, чтобы номинальная ставка была равна 6,8%. 4) Требуемая реальная ставка, согласно условию 5,5%. По формуле определяем обеспечивающую ставку: 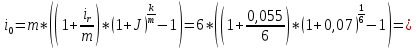 12,36% 12,36%То есть для того, чтобы реальная сумма вклада росла на 5,5% в год, необходимо, чтобы номинальная ставка была равна 12,36%. Основные результаты решения Задания 5
Задание 6 У предпринимателя есть ценная бумага, гарантирующая выплату по ней в размере P рублей через n лет. Предприниматель, желая получить деньги прямо сейчас, переуступает это обязательство банку. Банк согласен принять данную ценную бумагу с дисконтом i % годовых. Определить, какая сумма будет выплачена предпринимателю, если дисконтирование будет осуществлено по следующим схемам: а) по правилу математического дисконтирования с простым процентом; б) по правилу математического дисконтирования со сложным процентом; в) по правилу банковского учета с простым процентом; г) по правилу банковского учета со сложным процентом. Для вариантов, в которых получатся отрицательные значения, прокомментировать их. Данные для расчетов в задании 6: P=(a+b+5)*50000=(1+2+5)*50000=400000 i=0,1*(a+b)+4=0,1*(1+2)+4=4,3 n=b+4=2+4=6 Решение: 1) Математическое дисконтирование по простому проценту 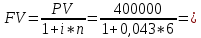 317965,02 руб. 317965,02 руб.2) Математическое дисконтирование по сложному проценту 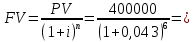 310709,22 руб. 310709,22 руб.3) Банковский учет по простому проценту  руб. руб.4) Банковский учет по сложному проценту 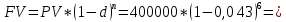 307278,11 руб. 307278,11 руб.Таким образом, предпринимателю выгоднее переуступить обязательство по ценной бумаге по правилу математического дисконтирования с простым процентом, так как по такой схеме он получит наибольший доход. Основные результаты решения Задания 6
Задание 7 У финансовой организации есть три варианта долгосрочного вложения средств: ВАРИАНТ 1 – вложить денежные средства в размере P1 руб. на 1 n лет в банк под 1 i % годовых с ежеквартальным начислением процентов; ВАРИАНТ 2 – вложить средства в размере P2 руб. на 2 n лет в проект, который принесет в конце срока не облагаемый налогом доход Q2 рублей; ВАРИАНТ 3 – вложить денежные средства в размере P3 рублей на 3 n лет в бизнес, который принесет в конце срока доход Q3 рублей, но нужно будет заплатить налог g3 % со всего полученного дохода. Определить, какой из вариантов вложения средств наиболее выгоден для финансовой организации, если операции оцениваются по правилу сложного процента. Вывод обосновать. Основные результаты решения оформить в виде вывода, примерно такого содержания: Вывод: финансовой организации выгоднее выбрать (1 или 2 или 3) вариант вложения денежных средств, потому что (краткое обоснование с приведением сравнения необходимых параметров). Данные для расчетов в задании 7: P1 a b 5*50000=(1+2+5)*50000=400000 P2 = (2*b+4)*40000=(2*2+4)*40000=320000 P3 = (50-5*a)*20000=(50-5*1)*20000=900000 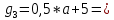 0,5*1+5=5,5 0,5*1+5=5,5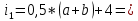 0,5*(1+2)+4=5,5 0,5*(1+2)+4=5,5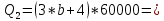 (3*2+4)*60000=600000 (3*2+4)*60000=600000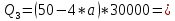 (50-4*1)*30000=1380000 (50-4*1)*30000=1380000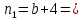 2+4=6 2+4=6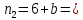 6+2=8 6+2=8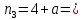 4+1=5 4+1=5Решение: Ответ на поставленный вопрос будем давать на основе сравнения эффективных процентных ставок. Так как операции длительные (от года и более), то будем использовать формулы для сложного процента. Так как из возможных схем только одна является стандартной, то лучше использовать общую формулу для определения эффективной годовой процентной ставки  где в данном случае PV – вложенные коммерсантом средства; FV – сумма, полученная коммерсантов в конце операции; n – срок операции в годах. Применим эту формулу для всех возможных вариантов деятельности: 1) В этом варианте PV=400000; n=6. Определим, какую сумму получит предприниматель через 6 лет по формуле сложного процента с начислением 4 раза в год (ежеквартально): 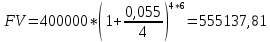 Тогда:  2) В этом варианте PV=320000; FV=600000; n=8. Тогда: 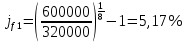 3) В этом варианте PV=900000; n=5. Для определения FV надо найти прибыль предпринимателя. После выплаты 5,5% налога у предпринимателя останется 900000-900000 *055 = 850500 руб. Тогда: 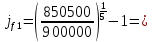 -1.12% -1.12%Чем выше годовая эффективная ставка, тем экономически выгоднее вариант вложения средств для предпринимателя. Наибольшая годовая эффективная ставка реализуется в первом варианте. Именно его и нужно выбрать предпринимателю. Вывод: финансовой организации выгоднее выбрать 1 вариант вложения денежных средств, потому что эффективная ставка равна 5,61%, которая является максимальной из всех вариантов. Задание 8 Государство Y просит в долг у государства X денежную сумму в размере P млрд. €. По взаимной договоренности установлена процентная ставка кредитной операции в размере i %. Согласно договору займа, долг должен быть возвращен двумя платежами: R1 млрд. € через 1n лет и R2 млрд. € через 2n лет. 1) Определить, какой должна быть сумма второго платежа R2 , при известной сумме первого платежа R1 млрд. €. Первый платеж выполнен вовремя в полном объеме. Но к моменту второго платежа 2n в государстве Y разразился экономический кризис, и оно настаивает на реструктуризации выплат. На переговорах государство-заемщик Y предлагает государству-кредитору X два варианта реструктуризации: ВАРИАНТ 1. Единым платежом в размере D млрд. € с переносом его на момент времени n3 лет от даты взятия в долг. ВАРИАНТ 2. Двумя равными платежами в размере S млрд. €, один в указанный в договоре момент времени 2 n лет от даты взятия в долг, а второй в момент времени n3 лет от даты взятия в долг. Государство-кредитор X вынуждено согласиться с каким-либо вариантом, иначе оно рискует не получить деньги вовсе. 2) Определить, какой из двух перечисленных вариантов будет выбран государством-кредитором X? 3) Изменилась ли его выгода от предоставленного кредита относительно исходных условий договора и в какую сторону? Основные результаты решения оформить в виде вывода, примерно такого содержания: Вывод: 1) Сумма второго платежа по договору займа должна быть равна (указать правильную сумму) млрд. €. 2) Государством-кредитором будет выбран (1 или 2) вариант реструктуризации, потому что (краткое обоснование с приведением сравнения необходимых числовых параметров). 3) Данный вариант реструктуризации выгоднее для (государства-кредитора или государства-заёмщика), потому что (краткое обоснование с приведением сравнения необходимых числовых параметров). Данные для расчетов в задании 8:
P=41; 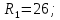 D=21; S=12; D=21; S=12;i= 3; 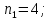 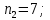 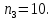 Решение: 1) Будем рассматривать ситуацию с точки зрения государства X. Тогда предоставляемый кредит будет иметь отрицательный знак (деньги уходят из государства Х), а все остальные платежи будут положительными (деньги при-ходят). Параметры финансового договора для примера таковы: i=3 %=0,03 R0= - 41 млрд. €..; R2 неизвестно; R1=26 млрд. €. n1=4 (кредит выдается вначале операции); n2 =7; n3=14 Приведем все величины к 7-му году и запишем уравнение баланса: 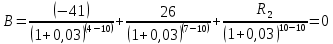 Тогда 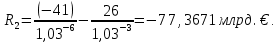 То есть второй платеж будет примерно равен -77,3671 €. 2) Для варианта 1 Составим баланс нового договора с позиции государства Х. В этом случае параметры договора будут равны: j=3 %=0,033 R1=26 млрд. €..; R2 = -70,80181 млрд. €.; n1=4; n2 =7; Баланс этого варианта договора равен 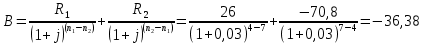 < 0 < 0Так как баланс, составленный с точки зрения кредитора, оказался отрицательным, можно сделать вывод, что данное изменение кредитору не выгодно и кредитор не согласится на предложенный вариант изменения договора. 3)Для варианта 2 Составим баланс нового договора с позиции государства Х. В этом случае параметры договора будут равны: j=3 %=0,03 R1=26 млрд. €..; R2 = -70,8 €.; R3 = R4=12 млрд. €. n1=4; n2 =7; n3=10 В качестве момента приведения можно использовать любую дату. Выберем датой приведения момент начала операции. Баланс договора равен: 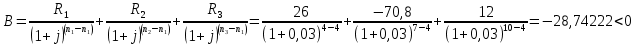 Как видно из баланса, этот вариант более выгодный исходного договора (так как баланс оказался менее отрицательным), и более выгоден, чем предыдущий вариант изменения. Вывод: 1) Сумма второго платежа по договору займа должна быть равна -77,36705€. 2) Государством-кредитором будет выбран 2 вариант реструктуризации, потому что он более выгоден 1 варианта. 3) Данный вариант реструктуризации выгоден для государства-кредитора, чем исходный вариант договора только для варианта 2, потому что его баланс менее отрицателен, а вариант 1 не выгодный, так как его баланс отрицательнее. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
