РГР Москаленко. Расчетнографическая работа Введение в теорию цепей Маркова

• Название: Расчетнографическая работа Введение в теорию цепей Маркова
• Дата: 10.05.2023
• Размер: 52.55 Kb.
• Имя файла: РГР Москаленко.docx
• Тип: Документы; #1120117

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное

учреждение высшего образования
«Ивановский государственный энергетический университет имени В.И. Ленина»
Кафедра прикладной математики
Расчетно-графическая работа

Введение в теорию цепей Маркова

Выполнил:

Москаленко Д.А. 1-1м

Проверил:

д.т.н., профессор

Беляков А.Н.

Иваново 2023

Студент ищет уравнение в методических указаниях для решения задачи. Всего 8 страниц. Он начинает искать уравнение с первой страницы. Искомое уравнение написано на 5ой и 8ой страницах МУ. Уравнение на странице 5 – правильное, а уравнение на 8 странице – с опечаткой. Ячейки 5 и 8 – поглощающие. Между другими ячейками студент ходит с определённой вероятностью. Нужно найти какая доля студентов найдёт правильное уравнение, а какая неправильное.

Изобразим исходную цепь с вероятностями переходов между ячейками: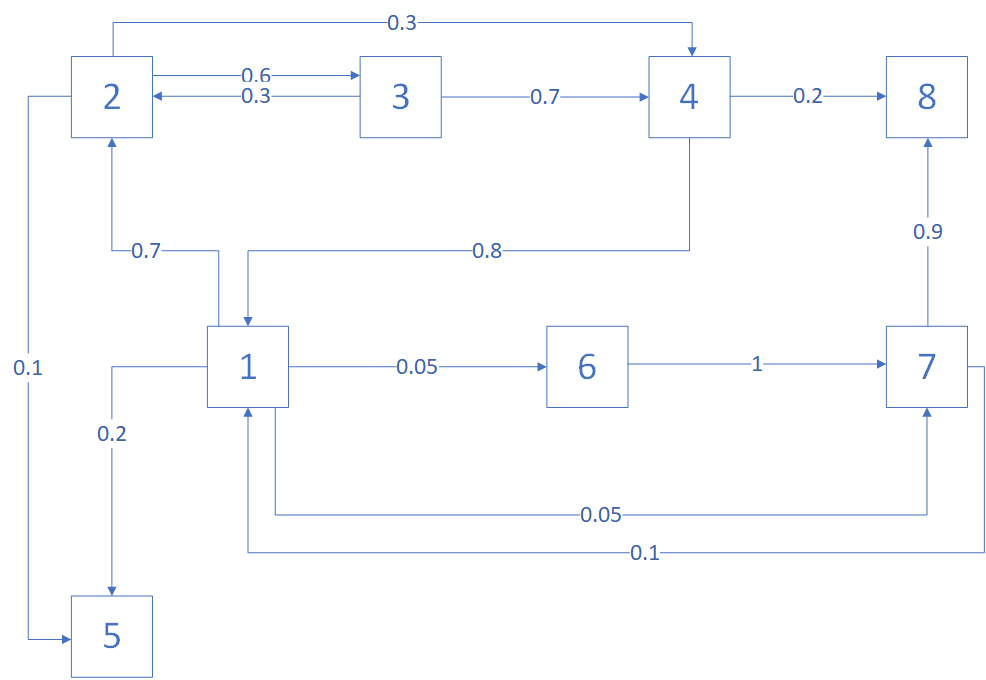



Составим матрицу переходных вероятностей P: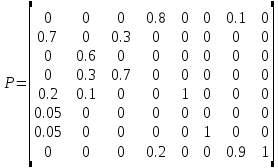



Начальный вектор состояния: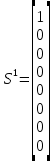



Организуем рекуррентную процедуру S^k+1=PS^k для различных значений параметра z.
Текст программы:

P = [0 0 0 0.8 0 0 0.1 0;

0.7 0 0.3 0 0 0 0 0;

0 0.6 0 0 0 0 0 0;

0 0.3 0.7 0 0 0 0 0;

0.2 0.1 0 0 1 0 0 0;

0.05 0 0 0 0 0 0 0;

0.05 0 0 0 0 1 0 0;

0 0 0 0.2 0 0 0.9 1;

];
S = [1 0 0 0 0 0 0 0]';

N=100;
for k=1:N

S = P * S;

%plot(k, S(8), '*b'); hold on;

ans1(k) = S(8);

ans2(k) = S(5);

end

figure(1);

subplot(2,1,1);

plot(ans1);

subplot(2,1,2);

plot(ans2);
Визуальное представление распределения студентов за 100 переходов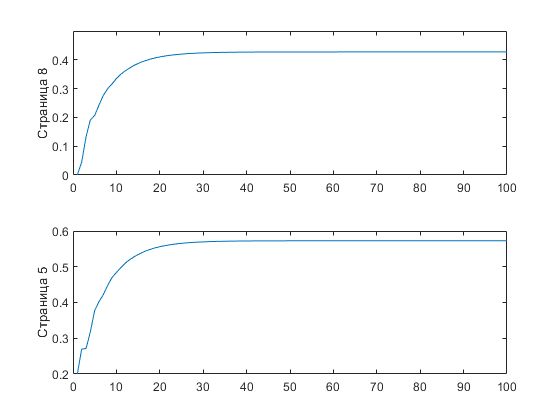



Вывод:

В работе была решена задача на тему «введение в теорию Марсковских цепей». Создана матрица вероятностей и начальный вектор состояния. Составлен граф и программа. Проведены эксперименты и получены итоговые зависимости.