Распространяется ли понятие надёжности на объект во время плановопредупредительных работ и ремонта
 Скачать 26.35 Kb.
|
|
Тест к экзамену Распространяется ли понятие надёжности на объект во время планово-предупредительных работ и ремонта: - Нет 2. Является ли исправным состояние машины, если она может выполнять свои функции, но не отвечает всем требованиям технической документации (например, помято крыло автомобиля): - нет 3. Какой вид долговечности задаётся техническим заданием на проектирование: - требуемая 4. Какой вид действительной долговечности определяет срок службы, за пределами которого проведение ремонтов данной машины становится экономически нецелесообразным: - моральная или - технико-экономическая 5. Свойство машины, заключающееся в её приспособленности к предупреждению, обнаружению, а также устранению отказов и неисправностей проведением ТО и ремонтов – это: - ремонтопригодность Показателем безотказности не является: - γ-процентный ресурс 7. К комплексным показателям надёжности относятся: - коэффициент технического использования - коэффициент готовности 8. Какая характеристика случайной величины определяет её разброс: - среднее квадратическое отклонение 9. Какой показатель случайной величины определяет наиболее вероятное её значение: - мода 10. Какой показатель случайной величины позволяет сравнить рассеивания величин, имеющих разную размерность - коэффициент вариации На испытание поставлено 1000 однотипных электронных ламп, за 3000 ч. отказало 80 ламп. Чему будет равняться вероятность безотказной работы P(t) при t = 3000 ч.? Ответ: 0.92 12. На испытание было поставлено 1000 однотипных ламп. За первые 3000 ч. отказало 80 ламп, а за интервал времени 3000-4000 ч. отказало еще 50 ламп. Чему будет равна интенсивность отказов электронных ламп в промежутке времени 3000-4000 ч.? Ответ: 5,6*10-5 1/час 13. На испытание было поставлено 1000 однотипных ламп. За первые 3000 ч. отказало 80 ламп, а за интервал времени 3000-4000 ч. отказало еще 50 ламп. Чему будет равна частота отказов электронных ламп в промежутке времени 3000-4000 ч.? Ответ: 5*10-5 1/час 14. На испытание поставлено 6 однотипных изделий. Получены следующие значения хi (хi - время безотказной работы i-го изделия): х1 = 280 ч; х2 = 350 ч; х3 = 400 ч; х4 = 320 ч; х5 = 380 ч; х6 = 330 ч. Определить статистическую оценку среднего времени безотказной работы изделия. Ответ: 343.3 час 15. На испытание поставлено N = 400 изделий. За время х = 3000 ч отказало 200 изделий, т.е. N(х) = 200. За интервал времени (х, х + Δх), где Δх = 100 ч, отказало 100 изделий, т.е. N(x + Δх)= 100. Требуется определить P(3100). Ответ: 0,25 Пусть поломка рессор автомобиля ГАЗ-3110 подчиняется нормальному закону с параметрами 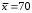 тыс. км и σ = 20 тыс. км. Определить вероятность безотказной работы рессор за пробег х = 50 тыс. км.Ответ: 0,84 17. Определить пробег рессоры автомобиля, при котором поломки составляют не более 20%, если известно, что 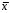 = 70 тыс. км и σ = 20 тыс. км.Ответ: 53.16 тыс км 18. Пусть интенсивность отказов подшипников скольжения λ = 0,0008 отказ/тыс. км. Определить вероятность безотказной работы подшипника за пробег 70 тыс. км, если известно, что отказы подчиняются экспоненциальному закону. P= 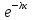 P=  19. При каком пробеге откажут 10 передач редукторов из 100, если отказы подчиняются экспоненциальному закону распределения? Интенсивность отказов составляет λ = 0,005 отказ/тыс. км. P(x)= 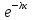=(100-10)/100=0.9 = =-0.105 (отказ)x=-0.105/-0.005=21 тыс.км 20. Пусть интенсивность отказов подшипников скольжения λ = 0,005. Определить наработку на отказ подшипника за пробег 30 тыс. км между пробегами 150 и 180 тыс. км и., если известно, что отказы подчиняются экспоненциальному закону. P= P=  21. При наблюдении за длительной период работы станции обслуживания установлено, что количество автомобилей, прибывающих на станцию, в среднем составляет 2 автомобилей в час. Определить вероятность поступления на станцию не более 8 автомобилей за t = 8 ч работы станции. P(m<8) =  a= λt = 2*8= 16 автомобилей P = 0,0000018 + 0,0000114 + 0,0000768 + 0,00031 + 0,00098 + 0,0026 + 0,0059 + 0,0119 = 0,0217 22. В результате наблюдений получено 120 значений случайной величины х. Наибольшее расхождение между теоретическим и расчётным значениями функции F(x) составляет Dn = 0,012. Необходимо оценить принадлежность распределения нормальному закону. - принадлежит 23. Требуется проверить близость некоторого фактического распределения с параметрами k = 8 и χ2 = 10,6 к нормальному. - соответствует R=6 Х^2(6)=12.6 10.6<12.6 24. Требуется определить необходимое количество двигателей, испытываемых на ресурсные показатели при δ = 10%, β0 = 0,95, если известно, что коэффициент вариации v = 0,32, а отказы подчиняются нормальному закону распределения.  по таблице из справочных материалов N=30.ОТВЕТ: 30 25. Требуется определить необходимое количество двигателей, испытываемых на ресурсные показатели при δ = 10%, β0 = 0,95, если известно, что коэффициент вариации v = 0,44, а отказы подчиняются закону распределения Вейбулла. при v = 0,44, b=2,4 (по таблице)  по таблице из справ. мат. N=60.ОТВЕТ: 60 26. Требуется определить необходимое количество двигателей, испытываемых на ресурсные показатели при заданной вероятности безотказной работы Р = 0,9, β0 = 0,95 при неизвестном законе распределения.  ОТВЕТ: 28 27. Для работы системы с последовательным соединением элементов при полной нагрузке необходимы два разнотипных насоса. Насосы имеют постоянные интенсивности отказов, равные λ1 = 0,0005 ч-1 и λ2 = 0,0006 ч-1 и подчиняются экспоненциальному закону распределения. Требуется определить вероятность безотказной работы данной системы в течение 200 ч. Предполагается, что оба насоса начинают работать в момент времени t = 0. Ответ: 0.8 28. Два одинаковых двигателя работают в системе с резервированием, причём если один из них выходит из строя, то другой способен работать при полной системной нагрузке. Найти безотказность системы в течение 800 ч при условии, что интенсивности отказов двигателей постоянны и равны λ = 0,0003 ч-1. Отказы двигателей статистически независимы, и оба двигателя начинают работать в момент времени t = 0. Ответ: 0.954 29. Система состоит из двух идентичных устройств, одно из которых функционирует, а другое находится в режиме ненагруженного резерва. Интенсивности отказов обоих устройств постоянны. Кроме того, предполагается, что в начале работы резервное устройство имеет такие же характеристики, как и новое. Требуется определить вероятность безотказной работы системы в течение 200 ч при условии, что интенсивности отказов данных устройств составляют λ = 0,0007 ч-1. Ответ: 0,869358 30. Данные испытания не являются контрольными: - аттестационные - ресурсные - исследовательские 31. Данные испытания не являются определительными - оценочные - предварительные - периодические - ресурсные - государственные 32. Какие испытания проводятся для проверки соответствия машины или сборочной единицы техническому заданию и технической документации? - предварительные 33. Какие испытания проводят для контроля стабильности качества производимой продукции? - периодические 34. Какие испытания проводят для решения вопроса о целесообразности постановки изделия на производство и ввода его в эксплуатацию? - государственные 35. Перечислите субъективные факторы, влияющие на надёжность машин. - выбор конструкторского решения при проектировании машины - рабочие режимы - организация ТО и Р 36. Перечислите объективные факторы, влияющие на надёжность машин. - климатические воздействия - механические воздействия 37. Перечислите конструктивные методы повышения надёжности машин - агрегатирование - упрочнение деталей - резервирование 38. Перечислите технологические методы повышения надёжности машин - упрочнение деталей - контроль качества изготовления деталей 39. Перечислите методы повышения надёжности машин при эксплуатации - проведение периодических ТО - обкатка новых и отремонтированных машин - контроль и дефектация деталей |