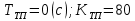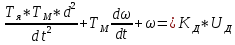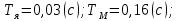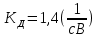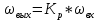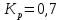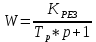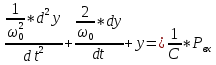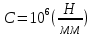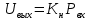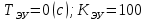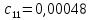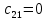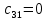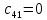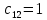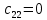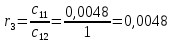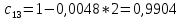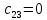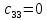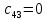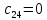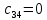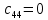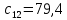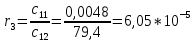Документ Microsoft Word (2). Рассчитать и проанализировать систему автоматического управления скоростью резанья при точении
 Скачать 2.67 Mb. Скачать 2.67 Mb.
|
  МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯРОССИЙСКОЙ ФЕДЕРАЦИИ ФГБОУ ВО «Брянский государственный технический университет» Политехнический колледж КУРСОВОЙ ПРОЕКТ по дисциплине: «МДК 04.01 Теоретические основы разработки и моделирования несложных систем автоматики с учетом спецификации технологических процессов» на тему: «Рассчитать и проанализировать систему автоматического управления скоростью резанья при точении» Всего 49 листов Студент гр. О-19-АТП-1: Коровин А.А. Преподаватель: Сергеева Е.Г. Брянск 2022 Содержание3 Раздел 1. Цели и задачи курсового проекта 5 Раздел 2. Конструктивная схема задание 6 Раздел 3. Передаточная функция элементов системы 7 Раздел 4. Функциональная и структурная схемы 10 Раздел 5. Расчет динамических характеристик 12 Раздел 6. Расчет устойчивости САУ. 23 Раздел 7. Определение показателей качества САУ 27 Раздел 8. Коррекция САУ 35 Заключение 36 Список литературы 37 Введение Раздел 1. Цели и задачи курсового проектаЦель выполнения курсового проекта - приобретение навыков самостоятельной работы при расчёте и анализе основных параметров заданной системы автоматического управления. Задачи курсового проекта: - правильно построить функциональную схему заданной системы автоматического управления; - правильно выделить типовые динамические звенья; - построить структурную схему системы автоматического управления с определением видосоединения типовых динамических звеньев; - определить передаточные функции всех элементов системы автоматического управления; - определение устойчивость заданной системы автоматического управления. - при необходимости провести коррекцию параметров с целью достижения устойчивости системы автоматического управления. - определение переходную характеристику замкнутой системы автоматического управления методом вещественных частотных трапециидальных характеристик или другим методом. - провести анализ системы автоматического управления по полученным характеристикам и сделать выводы. Раздел 2. Конструктивная схема задание«Рассчитать и проанализировать систему автоматического управления скоростью резания при точении» Исходные данные для проектирования: Конструктивная схема системы автоматического управления Обрабатываемая деталь 1 установлена в патроне 2 в заднем центре 3 токарного станка. В качестве двигателя 4 главного движения используется двигатель постоянного тока, для питания которого служит усилитель-преобразователь 5. Резец 6 установлен в тензометрическом динамометре 7 (типа УДМ-600), который связан с усилителем 8. В качестве преобразователя силы может быть использован динамометр другого типа, например, магнитоупругий. Суппорт 9 станка получает продольную подачу от коробки передач 10 с автономным двигателем 11. В систему входит сравнивающее устройство 12. В качестве объекта управления САУ включает в себя процесс резания (ПР) в замкнуто технологической системе станка (ТСС). 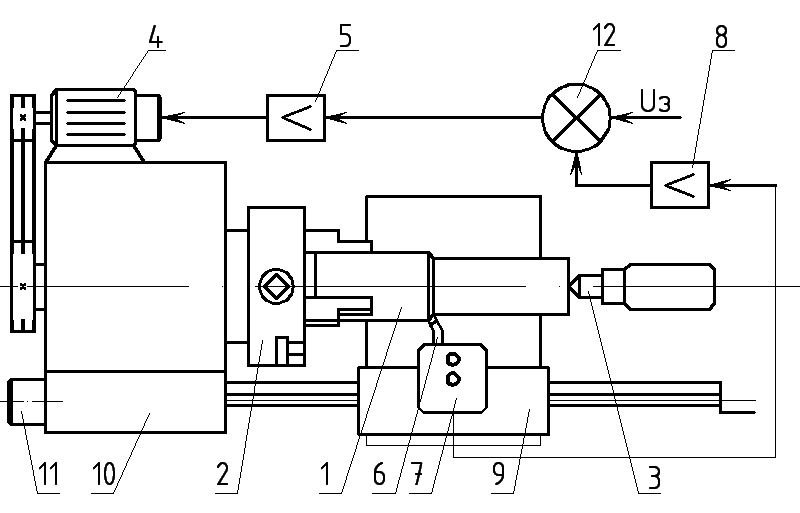 Рисунок 1 Конструктивная схема системы автоматического управления. Система автоматического управления скоростью резания при точении Раздел 3. Передаточная функция элементов системыТаблица 1 Заданные параметры элементов САУ
При определение передаточных функций звеньев в качестве входных принимать следующие дифференциальные уравнения движения. Тиристорный усилитель-преобразователь 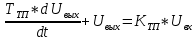 где 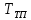 - постоянная выхода тиристорного преобразователя; - постоянная выхода тиристорного преобразователя;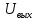 - выходное напряжение; - выходное напряжение; 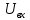 - входное напряжение; - входное напряжение; 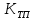 –коэффициент передачи (усиления). –коэффициент передачи (усиления).Электродвигатель постоянного тока 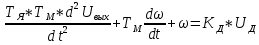 где 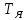 - электромагнитная постоянная времени якоря; - электромагнитная постоянная времени якоря;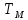 - электромеханическая постоянная двигателя; - электромеханическая постоянная двигателя;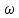 - угловая скорость; - угловая скорость; 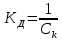 , ,Где  - коэффициент пропорциональности между обратной ЭДС и угловой скоростью; - коэффициент пропорциональности между обратной ЭДС и угловой скоростью;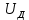 - напряжение якоря. - напряжение якоря.Механический редуктор 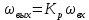 Где 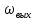 - угловая скорость выходного звена редуктора; - угловая скорость выходного звена редуктора;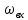 - угловая скорость входного звена редуктора; - угловая скорость входного звена редуктора;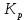 – коэффициент передачи. – коэффициент передачи.Процесс резания 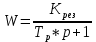 Где 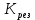 - коэффициент резания; - коэффициент резания;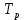 - постоянная времени стружкообразования. - постоянная времени стружкообразования.Технологическая система станка 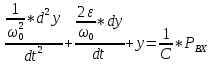 Где 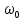 - собственная частота колебаний; - собственная частота колебаний; - коэффициент затухания колебаний; - коэффициент затухания колебаний;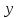 - деформация упругой системы станка; - деформация упругой системы станка; – жесткость упругой системы станка; – жесткость упругой системы станка; – входной силовой параметр. – входной силовой параметр.Преобразователь перемещения 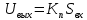 Где 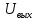 – выходное напряжение преобразователя; – выходное напряжение преобразователя;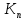 - коэффициент передачи; - коэффициент передачи;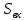 - выходное перемещение. - выходное перемещение.Усилитель  Где 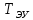 - постоянная выхода тиристорного преобразователя; - постоянная выхода тиристорного преобразователя;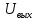 - выходное напряжение; - выходное напряжение; 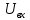 - входное напряжение; - входное напряжение; 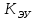 –коэффициент передачи (усиления). –коэффициент передачи (усиления).Раздел 4. Функциональная и структурная схемыСтруктурная схема САУ -это изображение системы регулирования в виде совокупности динамических звеньев с указанием связей между ними. Структурная схема САУ в простейшем случае строится из элементарных динамических звеньев. Структурная схема используется при математическом моделировании процесса управления. Она описывает основные составные части САУ с изображением типовых звеньев математическими правилами связей между ними и описываемых алгоритмами преобразования информации. Обратная связь(ОС) – это связь между выходом и входом системы или отдельного элемента внутри системы. Главная ОС – связь между выходом и входом системы. Местная ОС (коррекция) – это связь внутри системы, охватывающая один или несколько элементов.  Рисунок 2 Структурная схема системы автоматического регулирования скоростью резания при точении Функциональная схема САУ отображает устройства и элементы САУ более подробно, а также функциональные связи между ними. ТП-усилитель М-регулярный двигатель КП-коробка передач ПР – процесс резания ТСС – технологическая система станка ПС-тензометрический динамометр ЭУ-усилитель 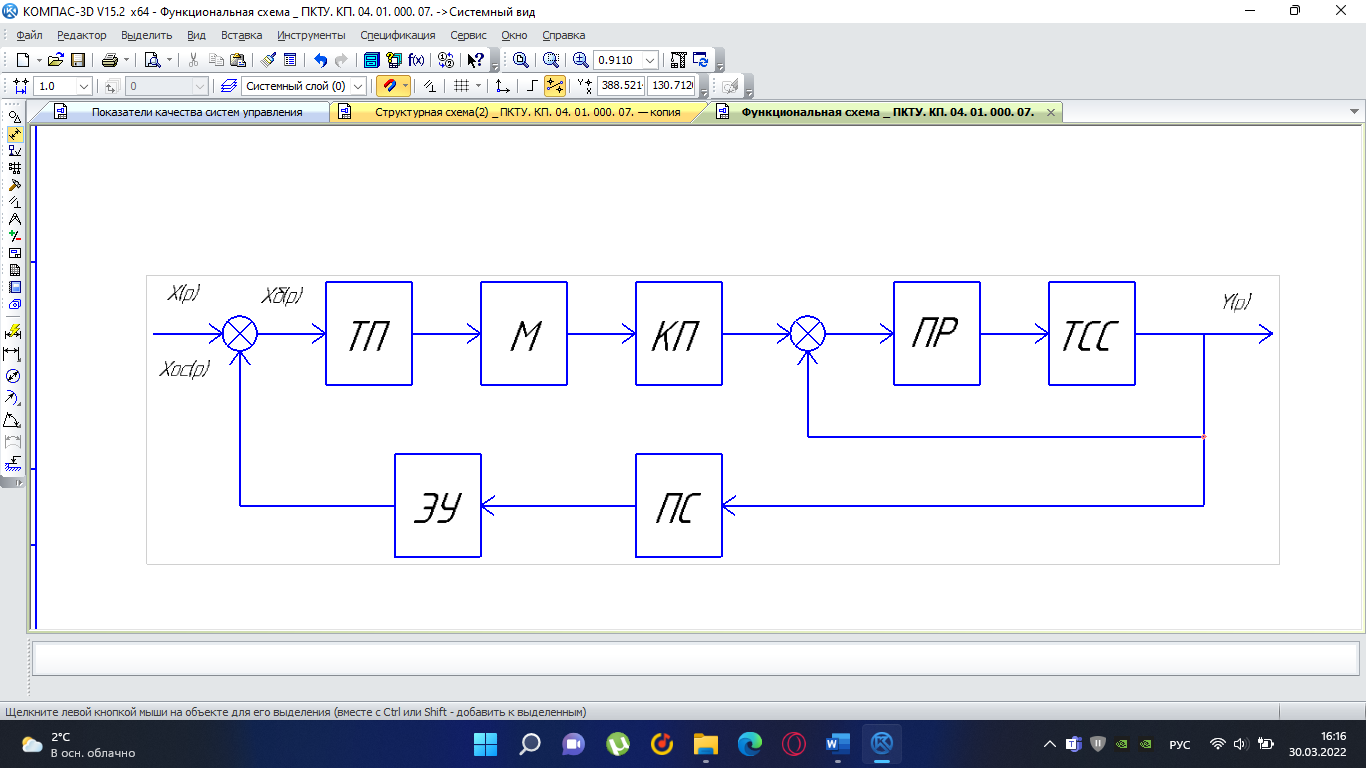 Рисунок 3 Функциональная схема системы автоматического регулирования скоростью резания при точении Раздел 5. Расчет динамических характеристикПередаточная функция – это отношение изображения выходного воздействия Y(p) к изображению входного X(p) при нулевых начальных условиях. Передаточная функция системы определяется видом соединения звеньев системы (последовательное, параллельное и параллельно-встречное). 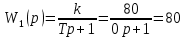 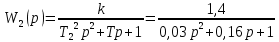 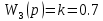 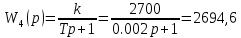  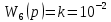   Рисунок 4. Нахождение передаточной функции для замкнутой и разомкнутой системы автоматического управления в Mathcad 15. 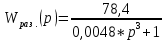 Частотная передаточная функция – замена оператора Лапласа на комплекс jω. 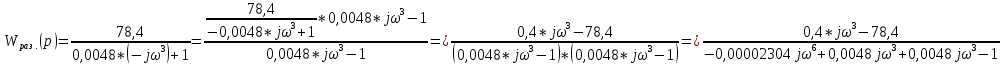 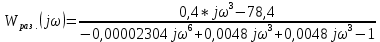 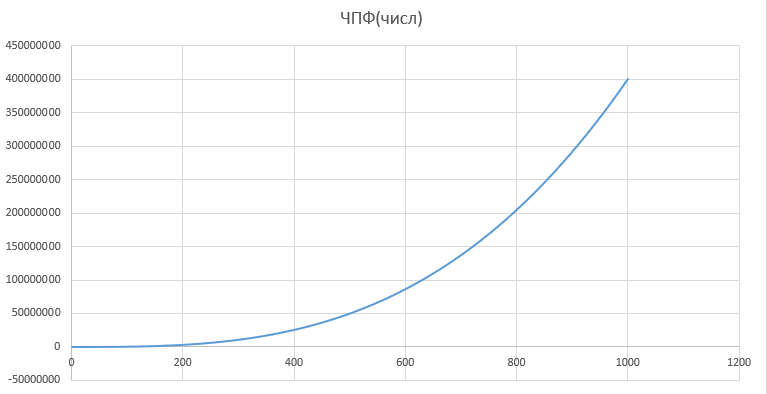 Рисунок 5. График частотной передаточной функции разомкнутой системы. Числитель.  Рисунок 6. График частотной передаточной функции разомкнутой системы. Знаменатель. Вещественная частотная характеристика (ВЧХ) 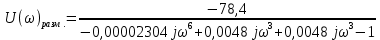  Рисунок 9. График ВЧХ разомкнутой системы. Мнимая частотная характеристика (МЧХ) 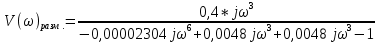 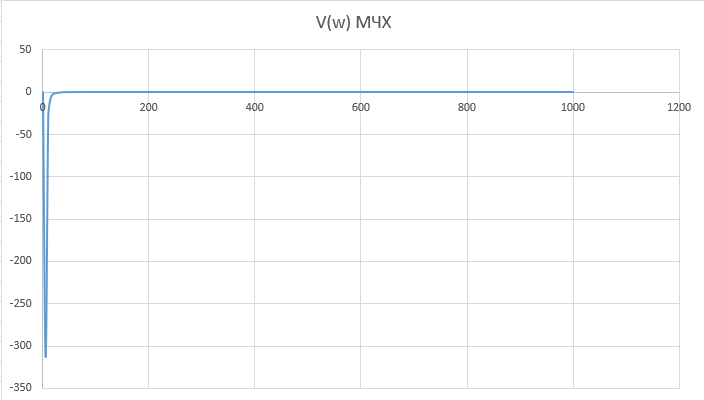 Рисунок 11. График МЧХ разомкнутой системы. Амплитудная частотная характеристика (АЧХ) -зависимость амплитуды установившихся колебаний выходного сигнала некоторой системы от частоты её входного гармонического сигнала. 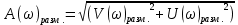  Рисунок 13. График АЧХ разомкнутой системы. Фазовая частотная характеристика (ФЧХ) - зависимость разности фаз между выходным и входным сигналами от частоты сигнала, функция, выражающая (описывающая) эту зависимость, также — график этой функции. 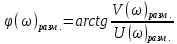 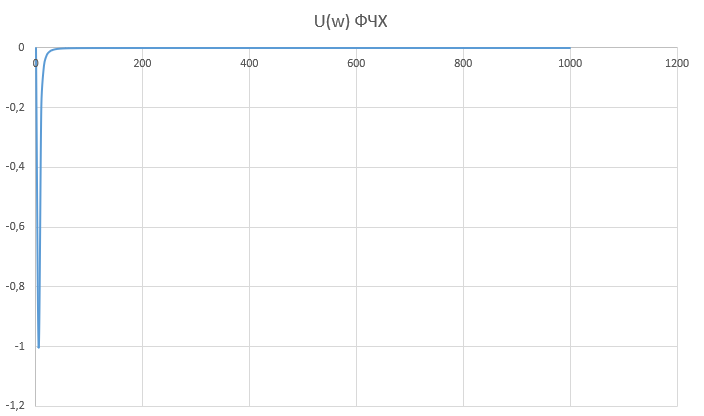 Рисунок 15. График ФЧХ разомкнутой системы. Амплитудная фазовая частотная характеристика (АФЧХ) –это геометрическое место точек описываемых концом вектора при изменении частоты от 0 до +∞ причем величина вектора равна амплитудной частотной характеристике, а угол поворота фазовой частотной характеристике. 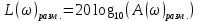 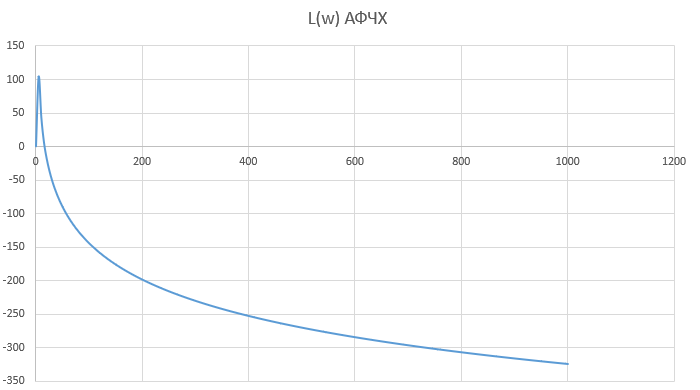 Рисунок 17. График АФЧХ разомкнутой системы. Логарифмическая амплитудная частотная характеристика (ЛАЧХ) – это кривая, соответствующая выражения 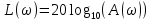 и построенная в логарифмическом масштабе частот. и построенная в логарифмическом масштабе частот.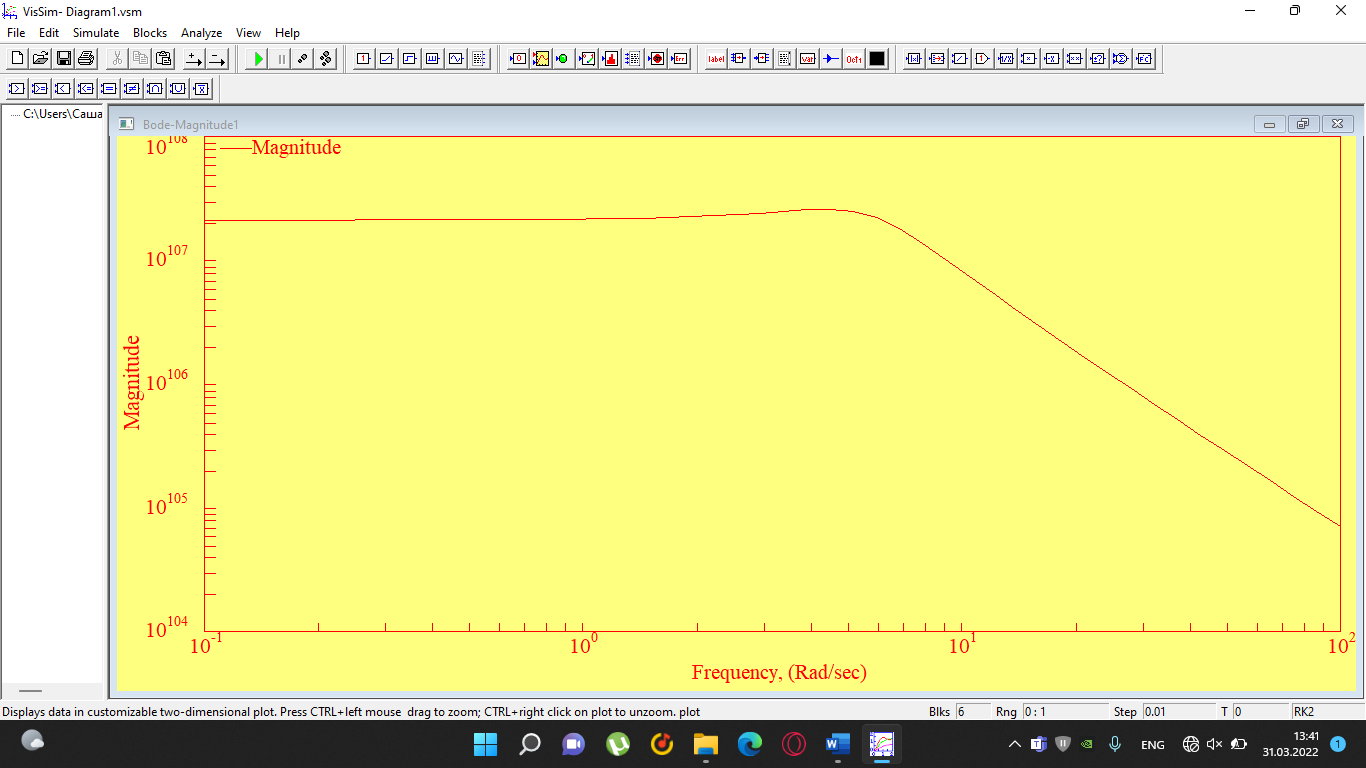 Рисунок 19. График ЛАЧХ разомкнутой системы. Логарифмическая фазовая частотная характеристика (ЛФЧХ) – это фазовая частотная характеристика φ(ω), построенная в логарифмическом масштабе частот. 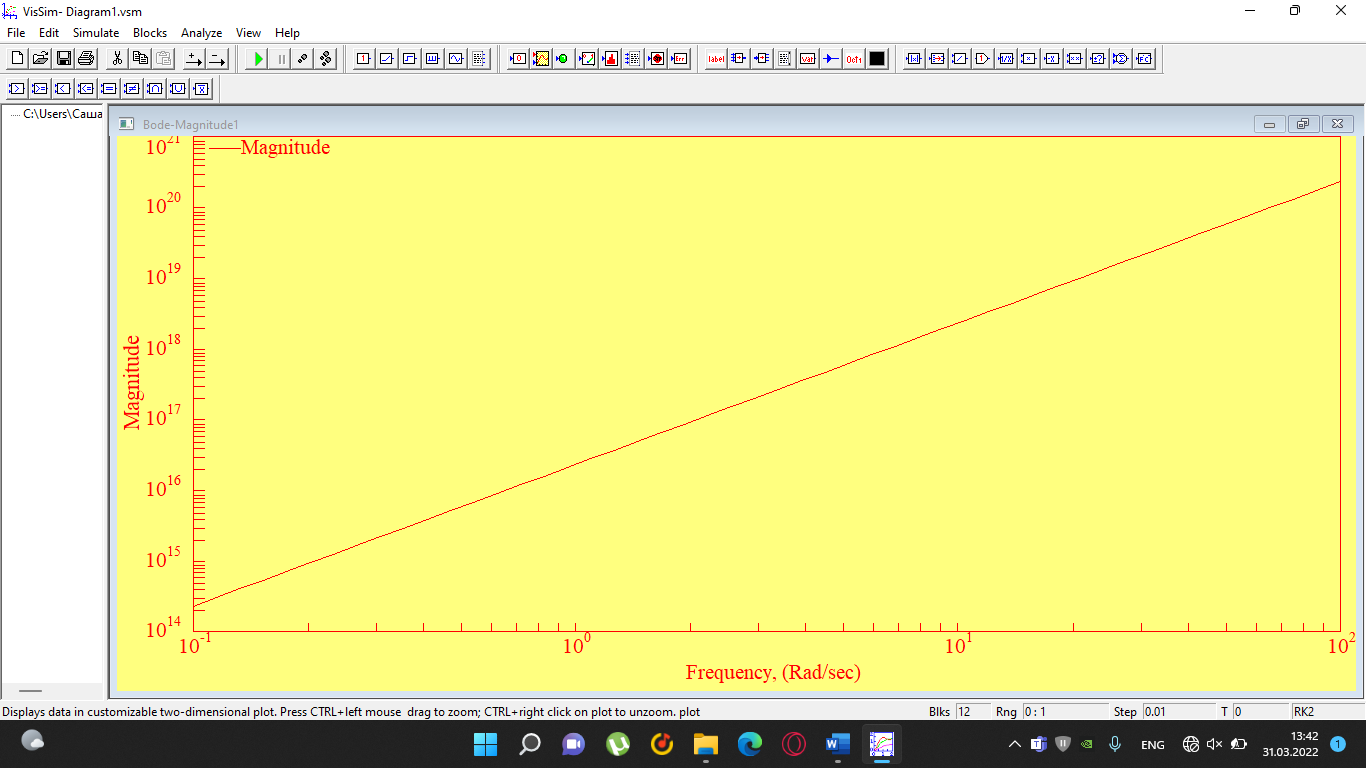 Рисунок 21. График ЛФЧХ разомкнутой системы. 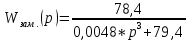  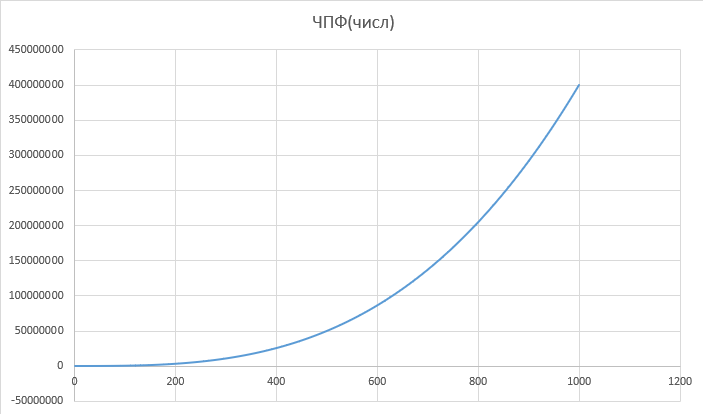 Рисунок 7. График частотной передаточной функции замкнутой системы. Числитель. 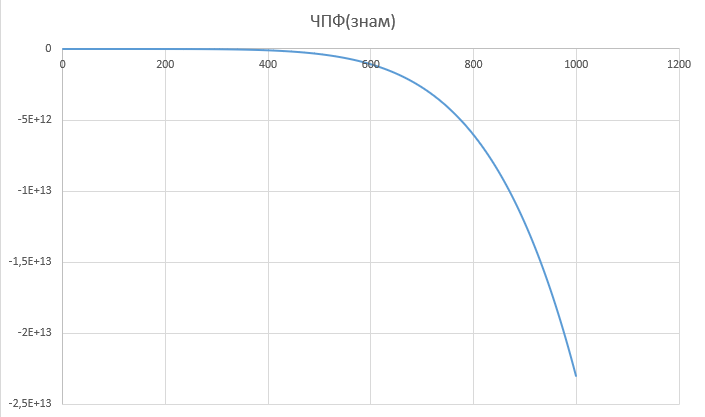 Рисунок 8. График частотной передаточной функции замкнутой системы. Знаменатель.  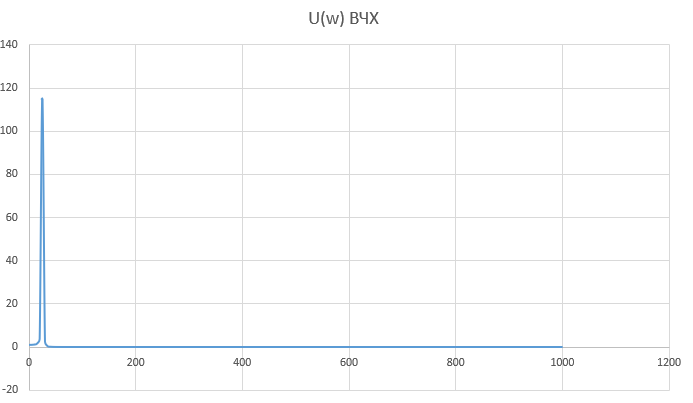 Рисунок 10. График ВЧХ замкнутой системы. 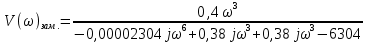 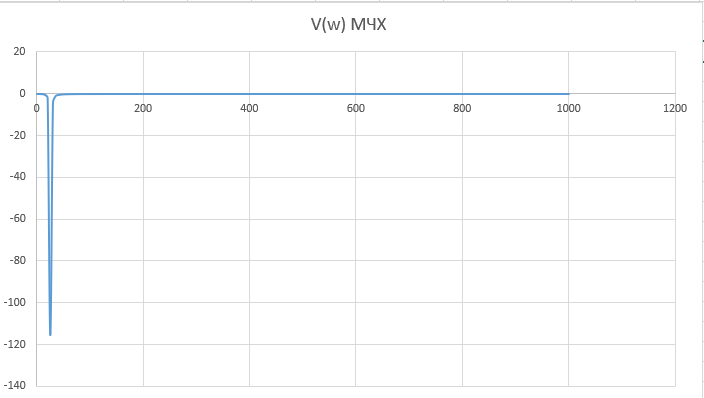 Рисунок 12. График МЧХ замкнутой системы. 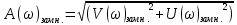 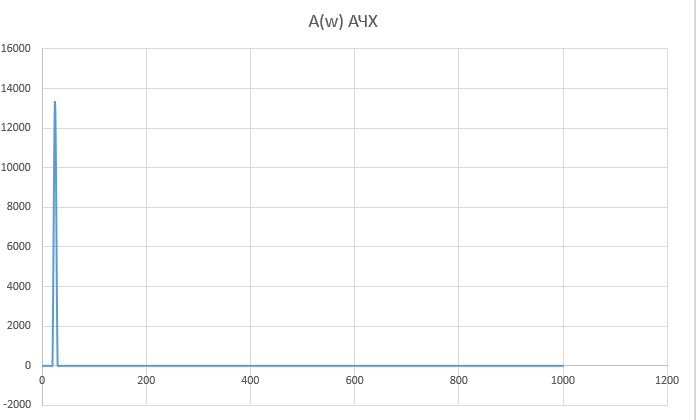 Рисунок 14. График АЧХ замкнутой системы.  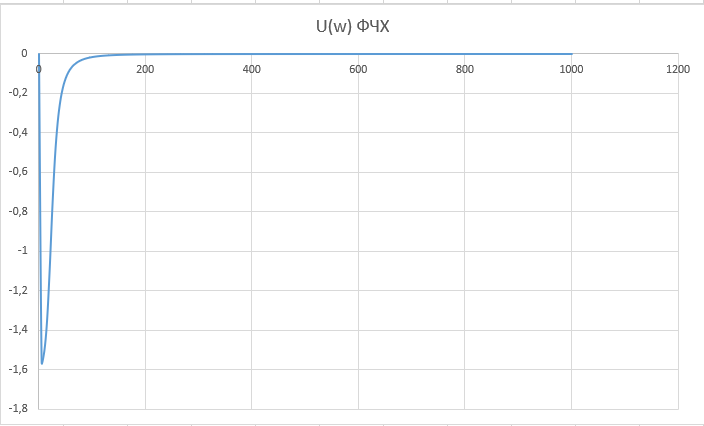 Рисунок 16. График ФЧХ замкнутой системы 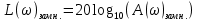 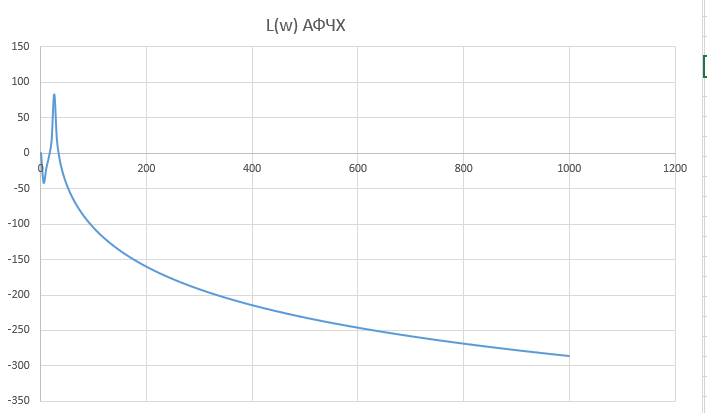 Рисунок 18. График АФЧХ замкнутой системы. 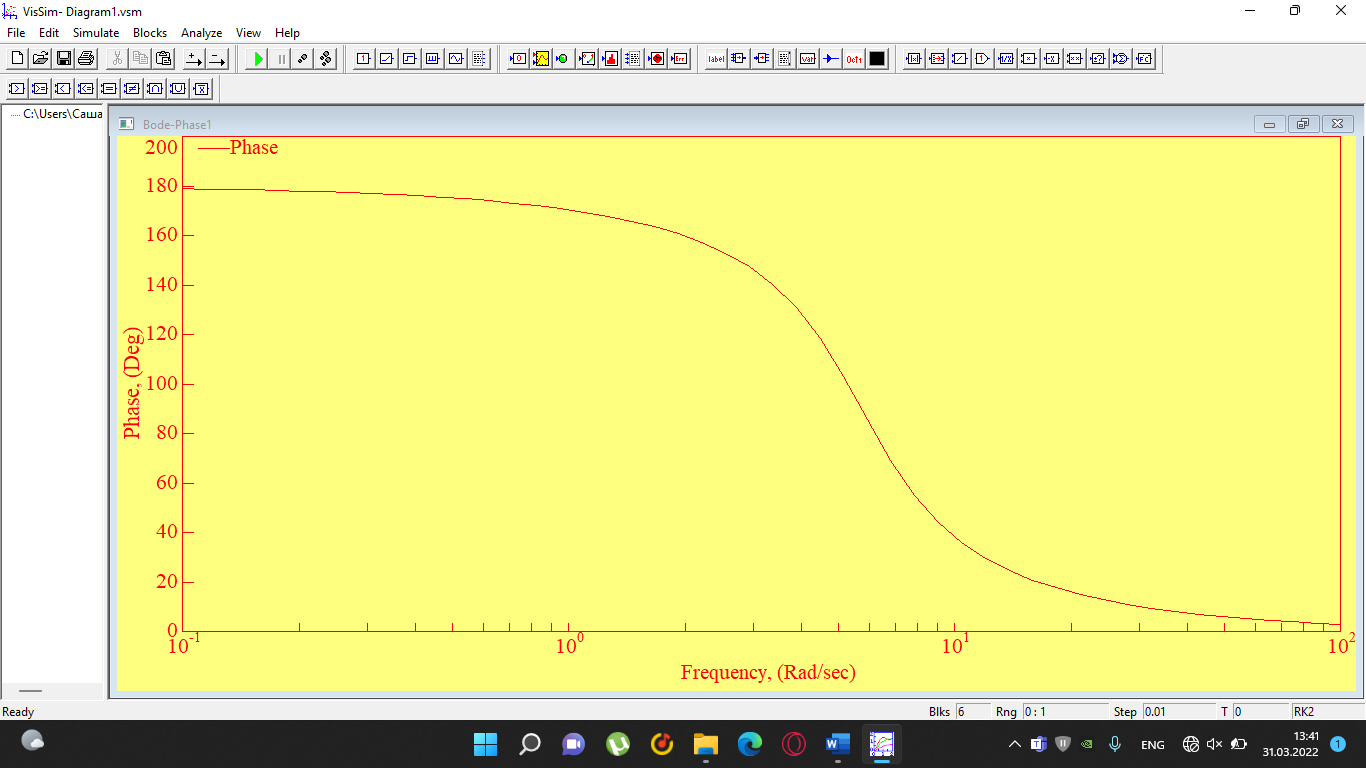 Рисунок 20. График ЛАЧХ замкнутой системы.  Рисунок 22. График ЛФЧХ замкнутой системы. Раздел 6. Расчет устойчивости САУ.Расчет критерии устойчивости по Раусу 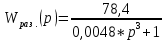 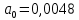 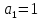 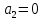 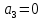 Таблица 2
Разомкнутая система является устойчивой по Раусу. 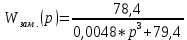 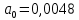 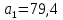 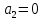 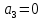 Таблица 3
Замкнутая система является устойчивой по Раусу. Чтобы система была устойчива, необходимо и достаточно, чтобы коэффициент первого столбца таблицы Рауса 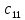 , , 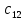 , ,  ,… была положительными. ,… была положительными.Расчет критерии устойчивости по Гурвицу 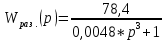 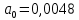 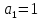 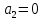 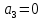  Разомкнутая система является на границе устойчивости по Гурвицу. 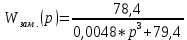 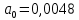 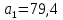 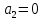 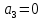  Замкнутая система является на границе устойчивости по Гурвицу. Чтобы система была устойчива, необходимо и достаточно, чтобы все коэффициенты характеристического уравнения и все n главных диагональных миноров матрицы Гурвицы были положительны. Расчет критерии устойчивости по Михайлову 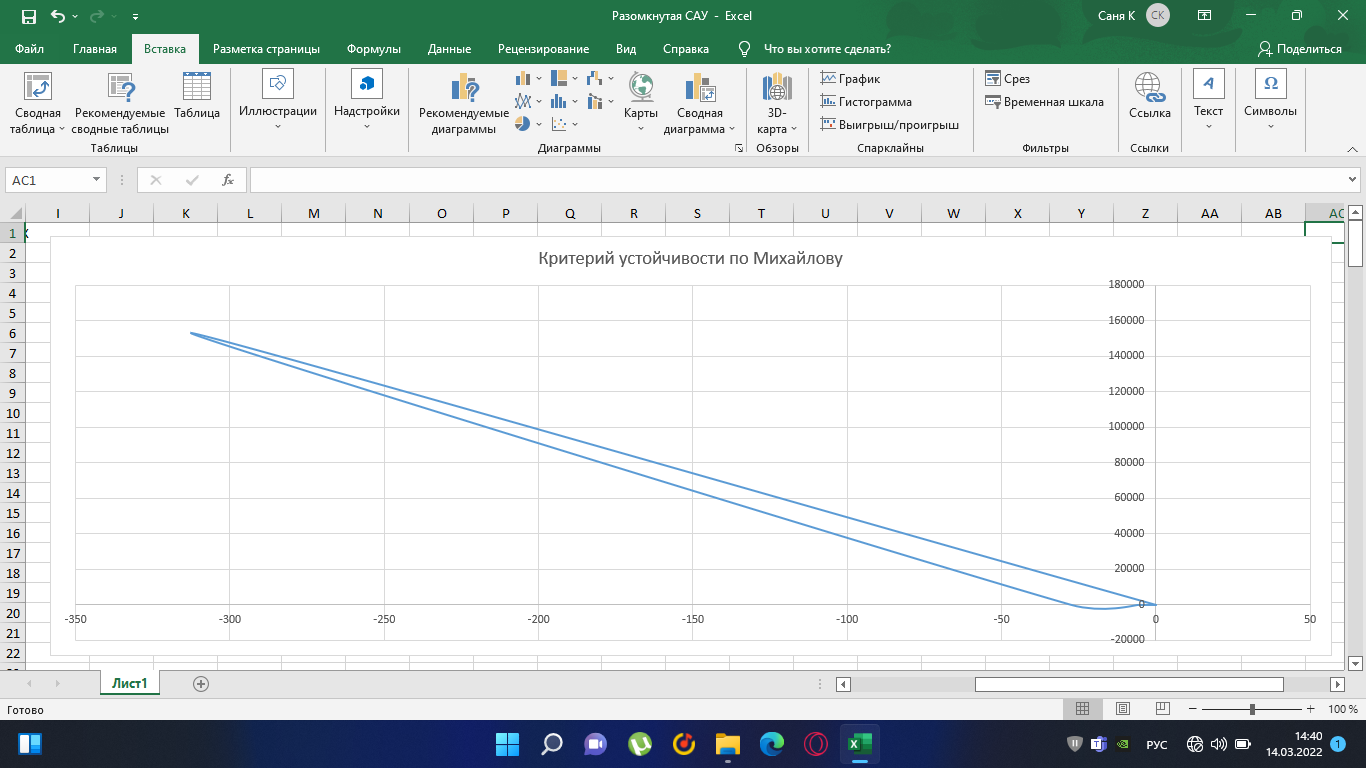 Рисунок 23. Расчет критерии устойчивости по Михайлову разомкнутой системы. Разомкнутая система является устойчивой по Михайлову. 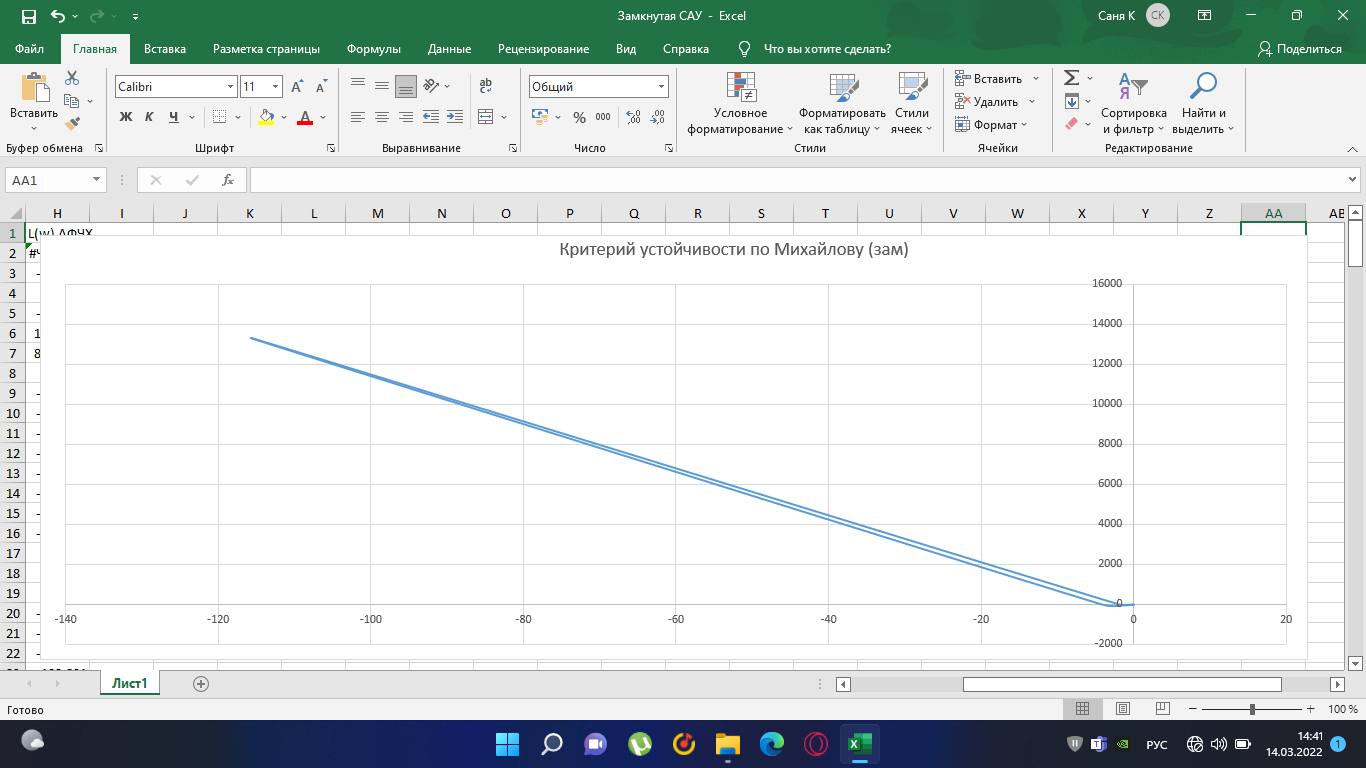 Рисунок 24. Расчет критерии устойчивости по Михайлову замкнутая системы. Замкнутая система является устойчивой по Михайлову. Если годограф начинается на положительной полуоси при 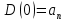 , и, при изменении частоты от 0 до , и, при изменении частоты от 0 до 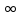 , последовательно проходит против часовой стрелки n квадрантов комплексной плоскости, с уходом в бесконечность в n- ом квадранте ни где не обращаясь в ноль, то такая система устойчива. , последовательно проходит против часовой стрелки n квадрантов комплексной плоскости, с уходом в бесконечность в n- ом квадранте ни где не обращаясь в ноль, то такая система устойчива.Расчет критерии устойчивости по Найквисту. 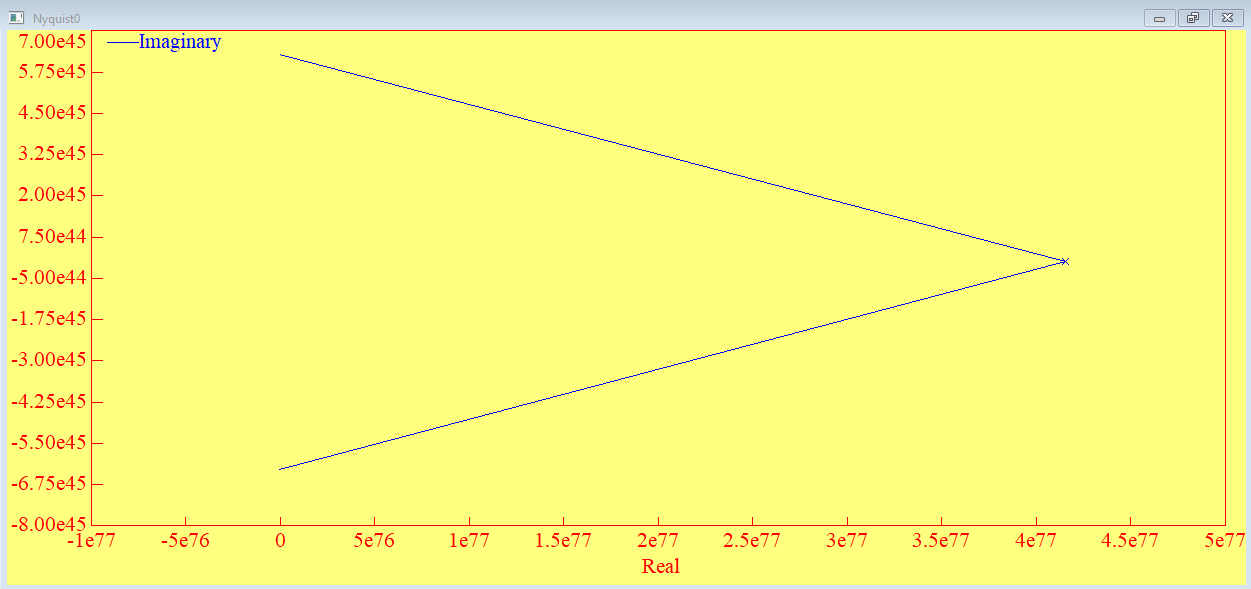 Рисунок 25. Расчет критерии устойчивости по Найквисту замкнутая системы. Замкнутая система является устойчивой по Найквисту. Линейная динамическая система устойчивая в разомкнутом состоянии, устойчива и в замкнутом состоянии, если АФЧХ разомкнутой системы 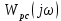 при изменении частоты от 0 до при изменении частоты от 0 до  не охватывает на комплексной плоскости точку с координатами (-1; j0) (годограф 1); линейная динамическая система, неустойчивая в разомкнутой состоянии, устойчива в замкнутом состоянии, если АФЧХ разомкнутая система не охватывает на комплексной плоскости точку с координатами (-1; j0) (годограф 1); линейная динамическая система, неустойчивая в разомкнутой состоянии, устойчива в замкнутом состоянии, если АФЧХ разомкнутая система  при изменении частоты от от 0 до при изменении частоты от от 0 до  охватывает на комплексной плоскости точку с координатами (-1; j0) столько раз, сколько корней характеристического уравнения лежит справа от мнимой оси на комплексной плоскости корней (годограф 2). охватывает на комплексной плоскости точку с координатами (-1; j0) столько раз, сколько корней характеристического уравнения лежит справа от мнимой оси на комплексной плоскости корней (годограф 2).Раздел 7. Определение показателей качества САУРассчитаем показатели качества систем управления Передаточная функция дифференциальном виде 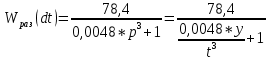 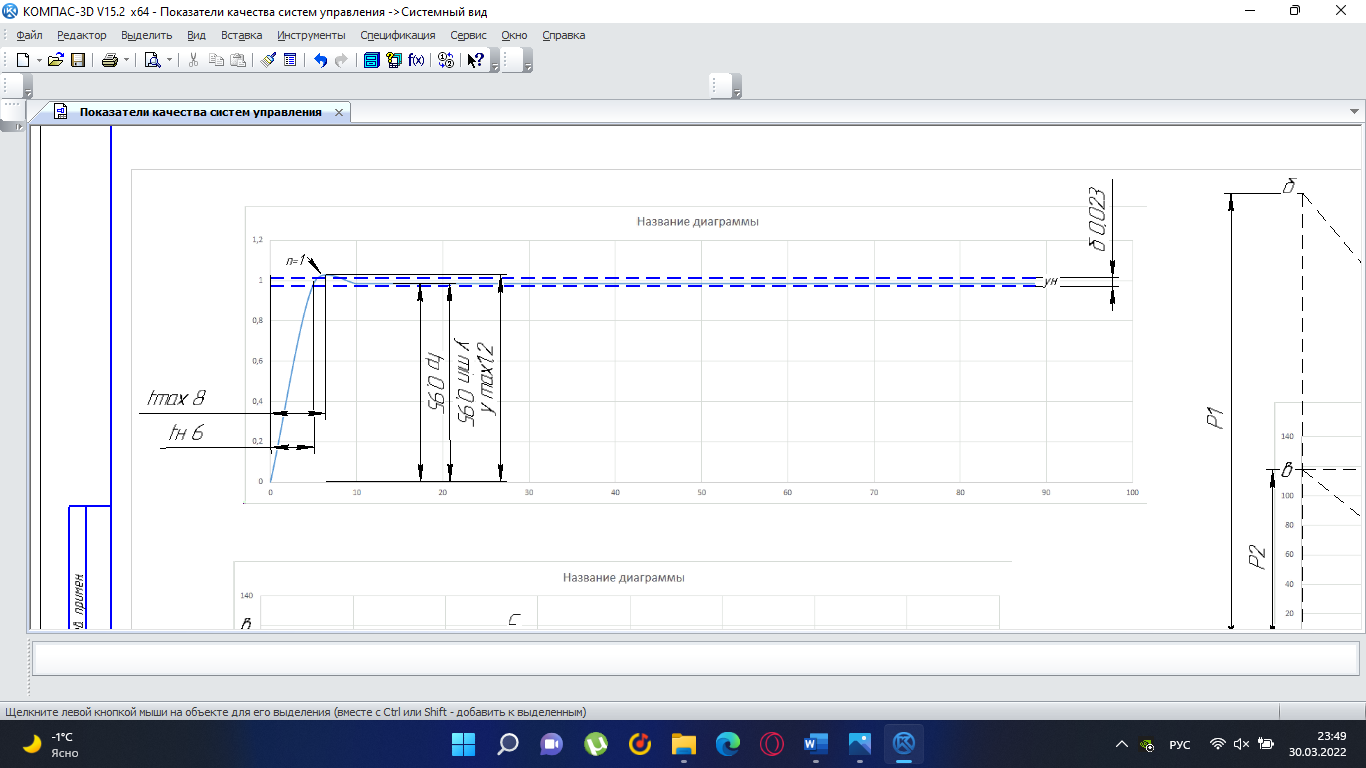 Рисунок 36. Показатели качества систем управления в КОМПАСЕ Установившееся значение регулируемого параметра - 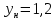 ; ;Время регулирования - 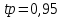 ; ;Величина перерегулирования - 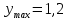 ; ;Установившаяся регулирования - 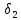 =0,023 =0,023Колебательность переходного процесса -M Число колебаний за время регулирования -n=1 Время нарастания - 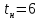 Время достижения первого максимума - 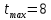 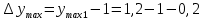  Косвенные методы оценки качества Оценка качества переходного процесса по амплитудо-частотной характеристике замкнутой системы с единичной обратной связью.   Рисунок 27. График оценки качества переходного процесса по амплитудо-частотной характеристике замкнутой системы с единичной обратной связью через формолу OA в Excel 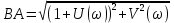  Рисунок 28. График оценки качества переходного процесса по амплитудо-частотной характеристике замкнутой системы с единичной обратной связью через формолу BA в Excel. 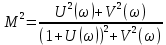 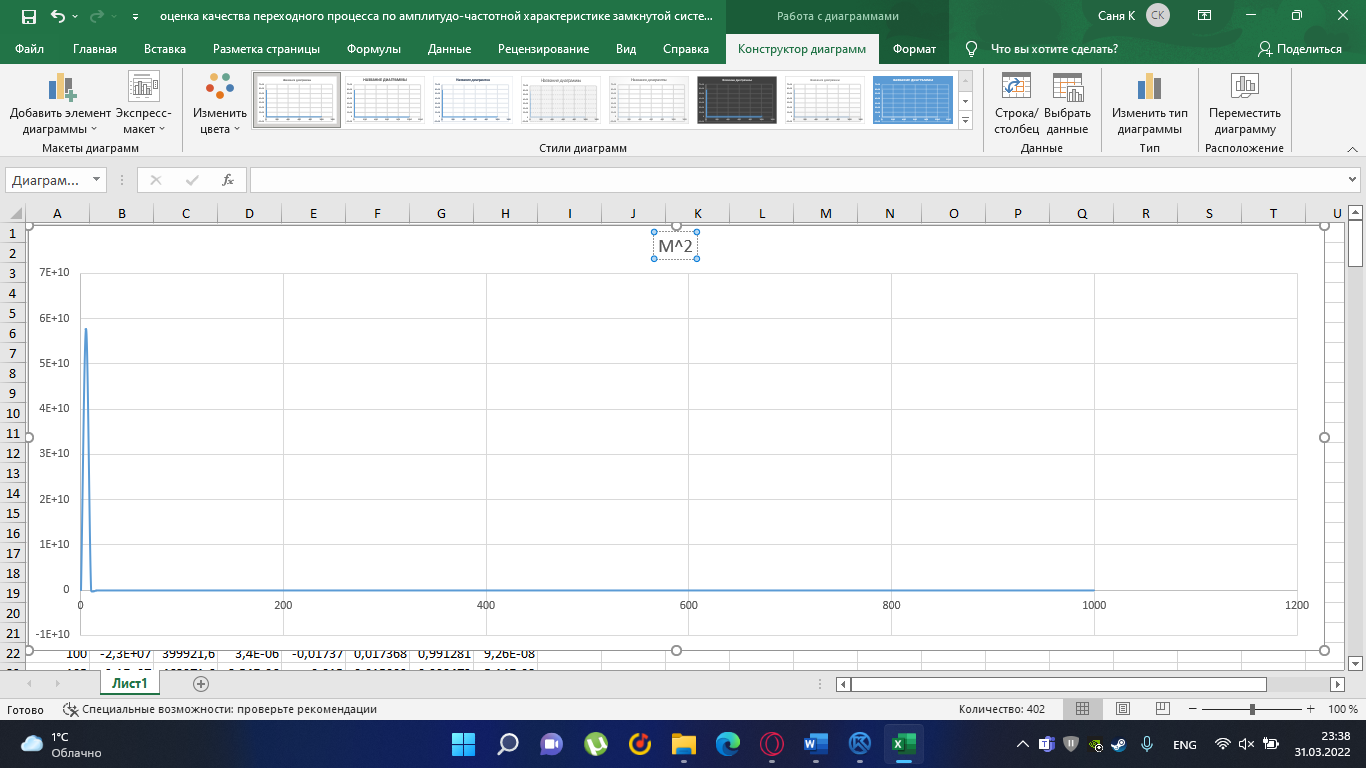 Рисунок 29. График оценки качества переходного процесса по амплитудо-частотной характеристике замкнутой системы с единичной обратной связью через формолу  в Excel в Excel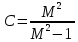 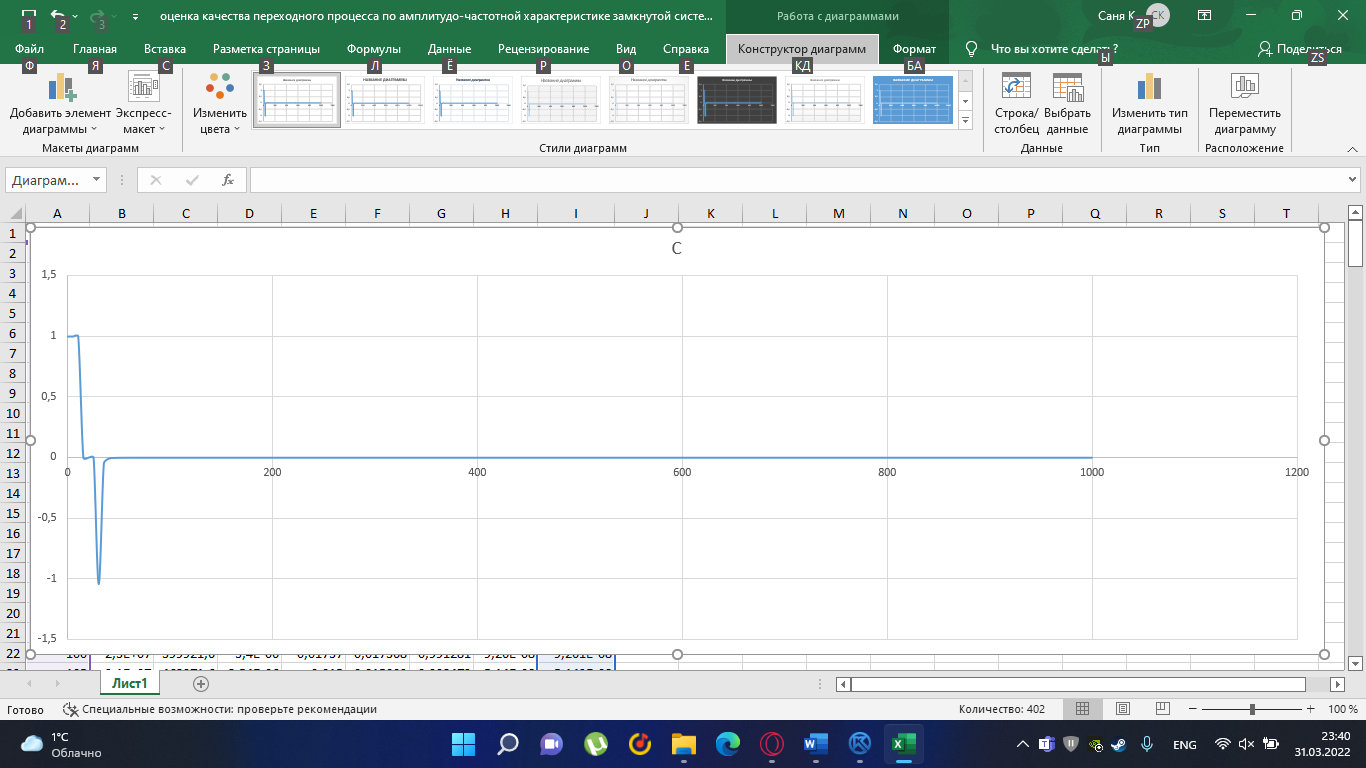 Рисунок 30. График оценки качества переходного процесса по амплитудо-частотной характеристике замкнутой системы с единичной обратной связью через формолу C в Excel  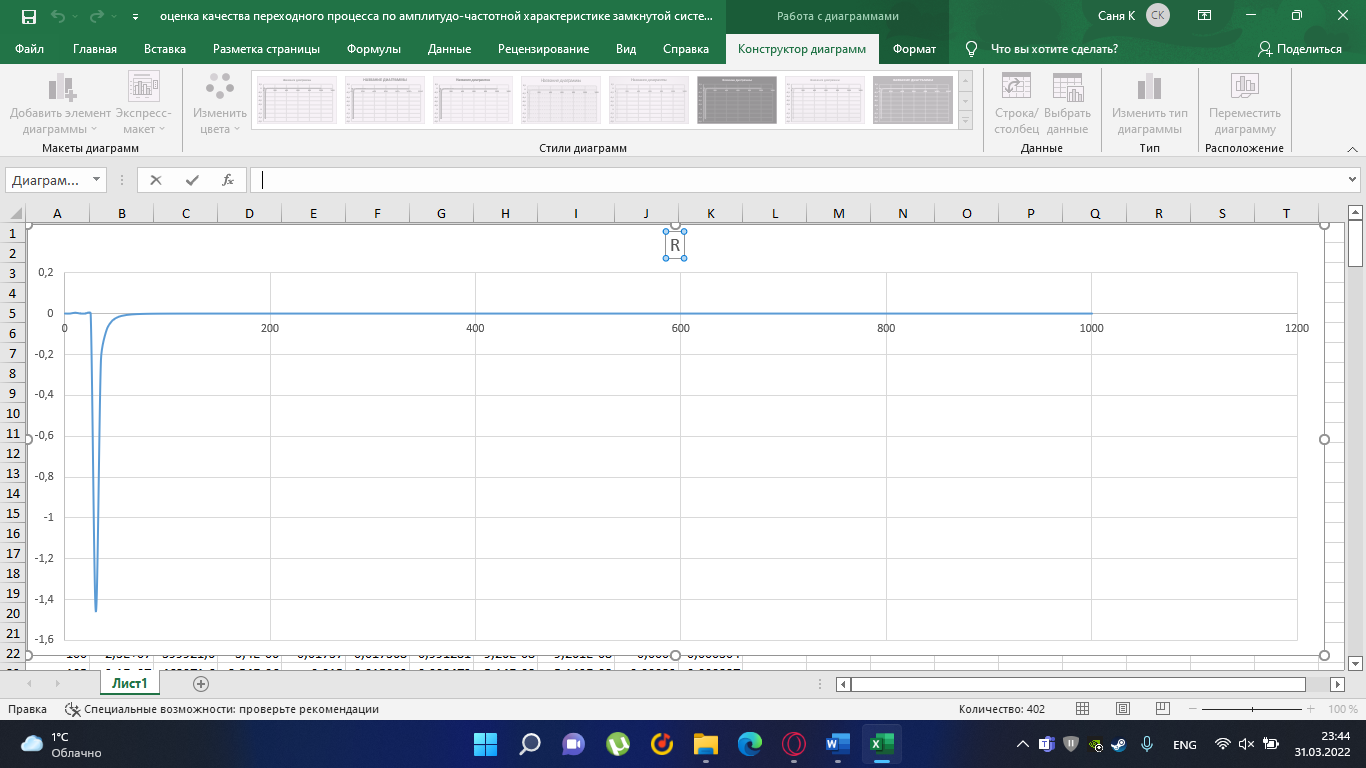 Рисунок 31. График оценки качества переходного процесса по амплитудо-частотной характеристике замкнутой системы с единичной обратной связью через формолу R в Excel Оценка качества переходного процесса по диаграмме Вышнеградского 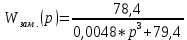 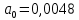 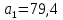   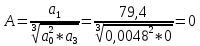   Рисунок 32. Диаграмма Вышнеградского Система является не устойчивой по диаграмме Вышнеградского, т.к. точка стоит (0;0). Корневой метод оценки качества 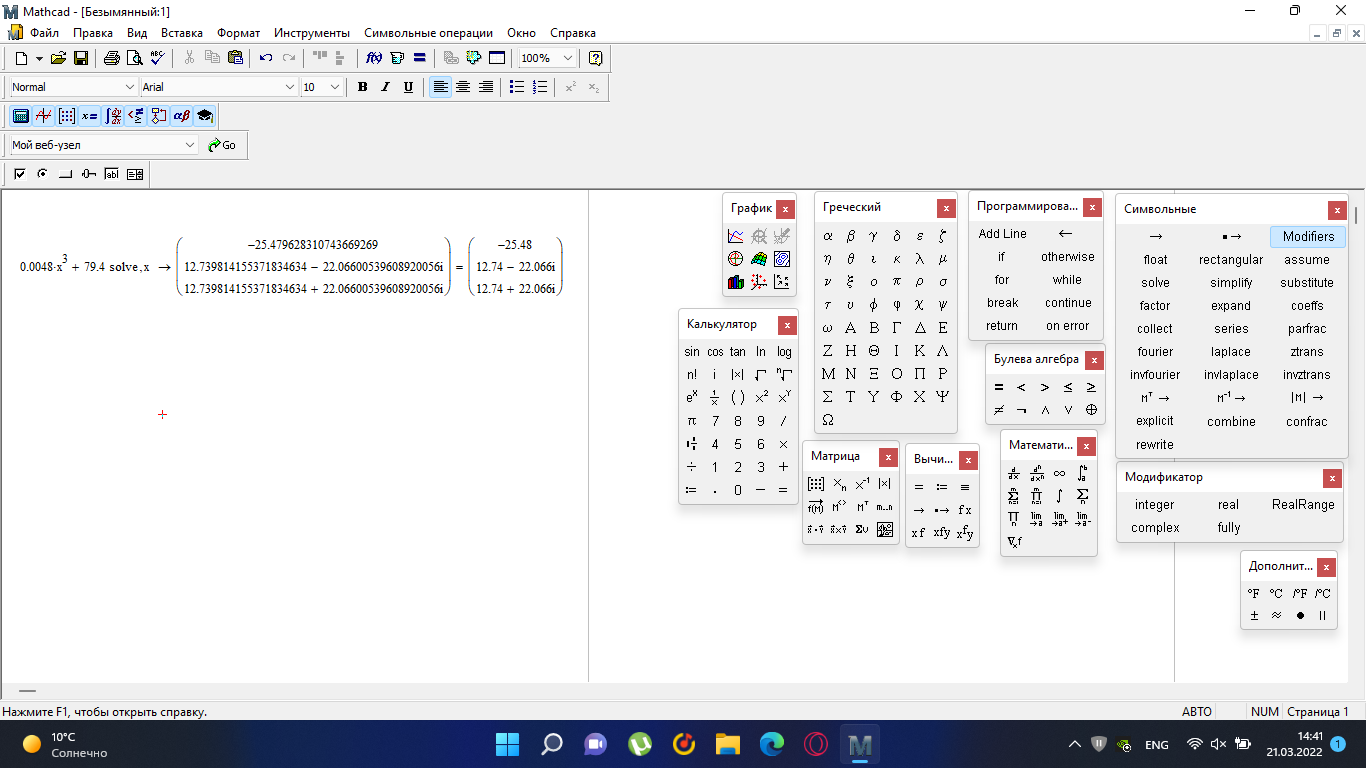 Рисунок 33. Расчет корневого метода в Mathcad 15. 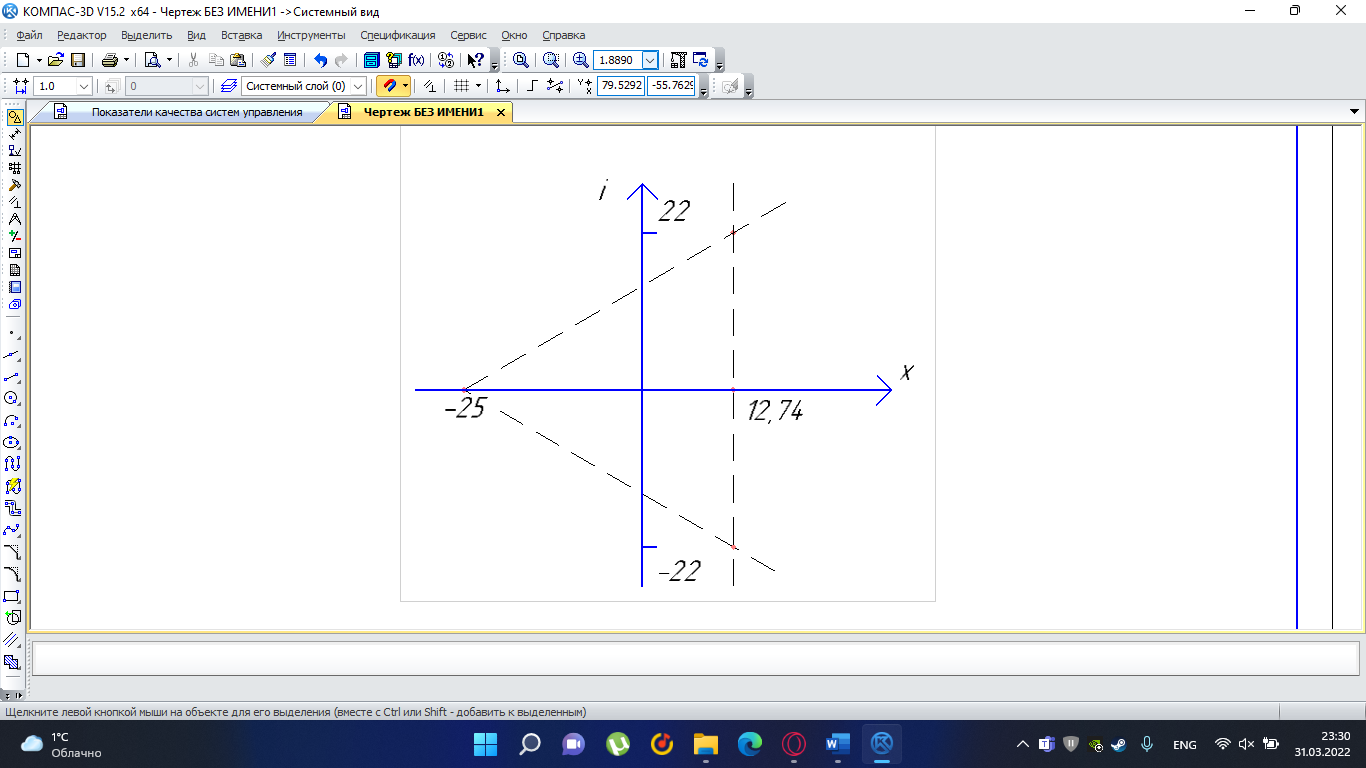 Рисунок 34. Корневой метод график (КОМПАС) Интегральный метод оценки качества 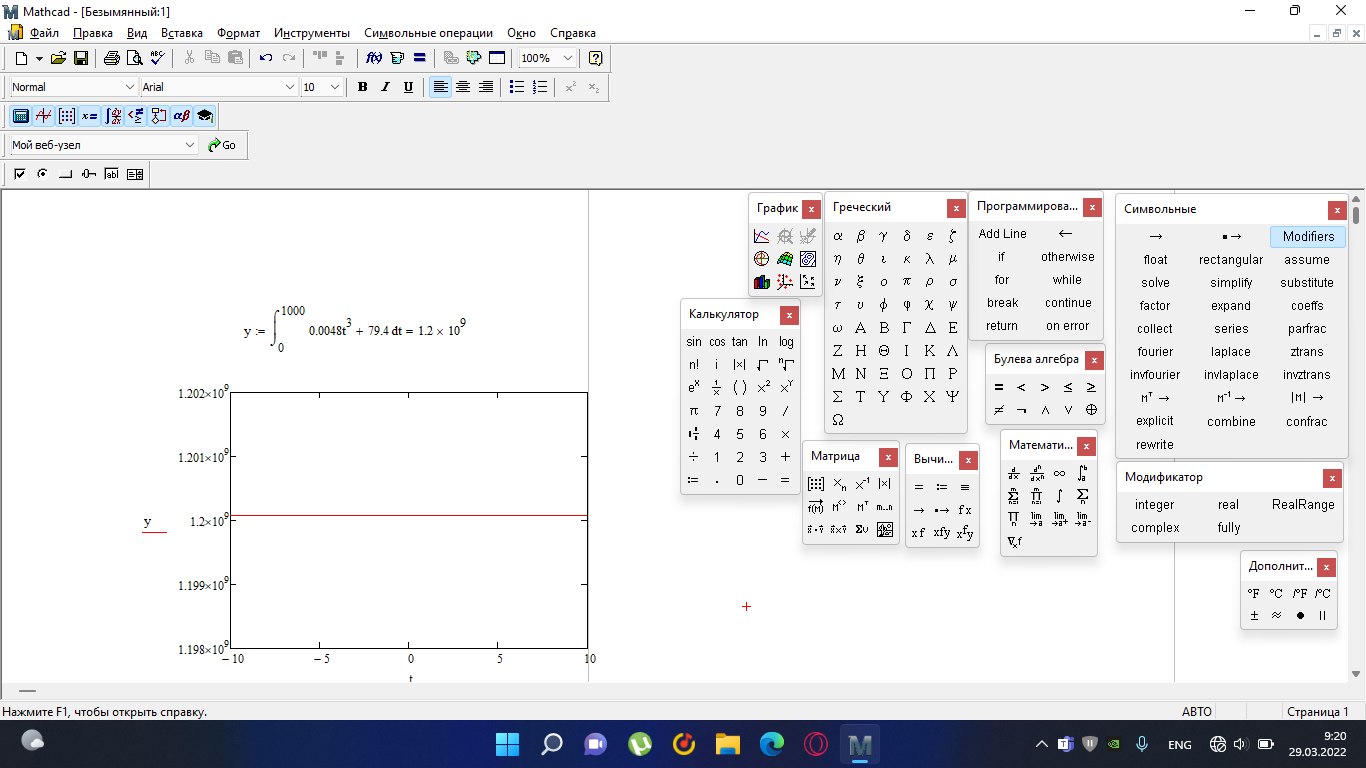 Рисунок 35. Расчет интегрального метода в Mathcad 15. Величина 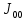 представляет собой линейную оценку качества управления. Чем меньше, тем выше быстродействие системы. При выборе параметров системы стремятся обеспечить минимум представляет собой линейную оценку качества управления. Чем меньше, тем выше быстродействие системы. При выборе параметров системы стремятся обеспечить минимум 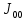 . .Прямые Трапеции Пусть передаточная функция системы имеет вид: 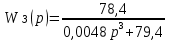 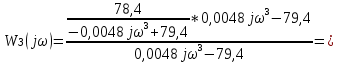 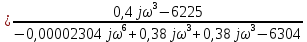 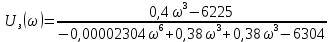
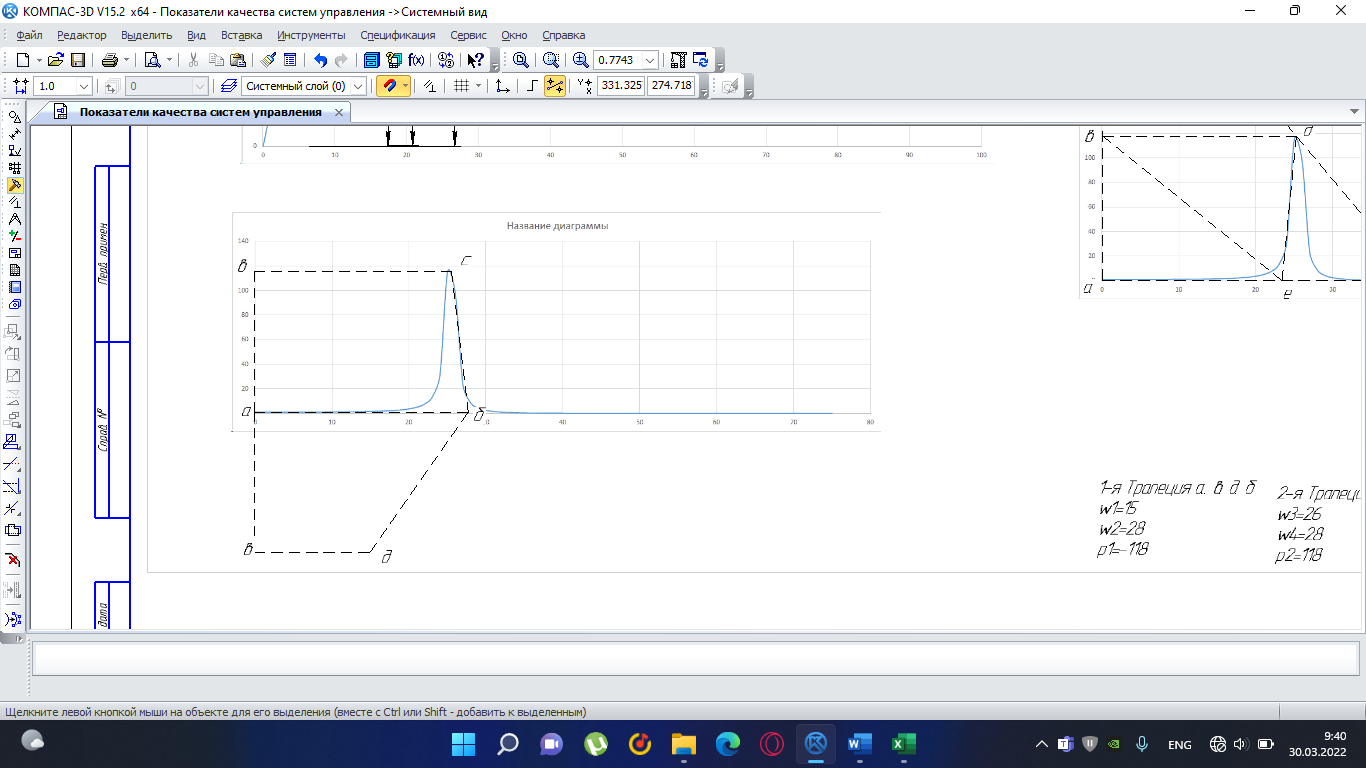 1-я трапеция а-в-д-б: 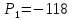 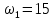  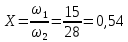 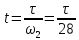 2-я трапеция а-б-в-с 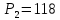 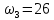 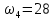 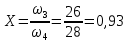 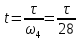 Треугольники 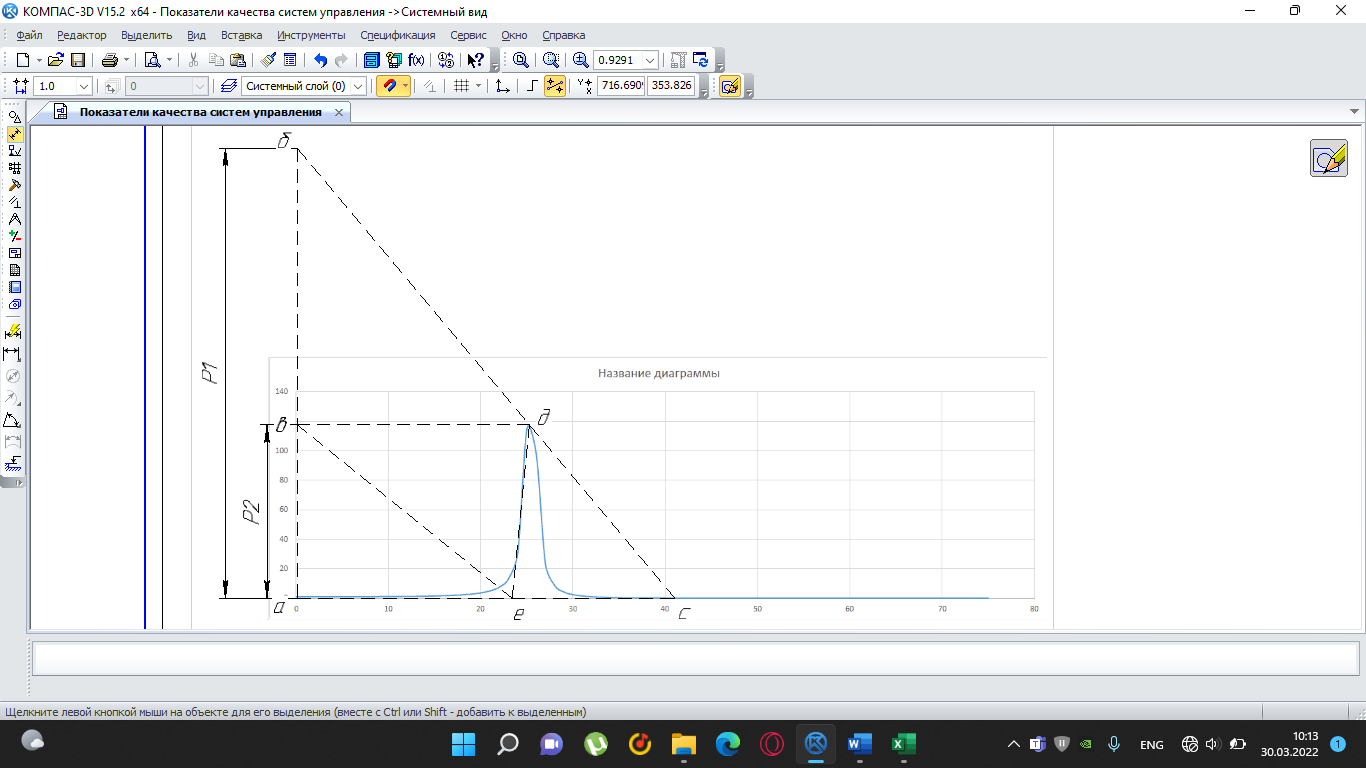 Треугольник 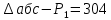 Треугольник  Раздел 8. Коррекция САУКорректирующие звенья – динамические звенья с определенным передаточными функциями. Т.к. данная САУ устойчева по всем алгебраическим и частотным критериям ,то корректировку САУ не требуется. ЗаключениеСписок литературы |