алгоритм Евклида. Расширенный алгоритм Евклида (1). Расширенный алгоритм Евклида

• Название: Расширенный алгоритм Евклида
• Анкор: алгоритм Евклида
• Дата: 01.11.2022
• Размер: 51.11 Kb.
• Имя файла: Расширенный алгоритм Евклида (1).docx
• Тип: Решение; #765629

Расширенный алгоритм Евклида

Даны два целых числа a и b. Нам зачастую надо найти другие два целых числа, s и t, такие, которые

s x a + t x b = НОД(a,b)

Расширенный алгоритм Евклида может вычислить НОД (a, b) и в то же самое время вычислить значения s и t. Алгоритм и процесс такого вычисления показан на рис. 2.8.

Здесь расширенный алгоритм Евклида использует те же самые шаги, что и простой алгоритм Евклида. Однако в каждом шаге мы применяем три группы вычислений вместо одной. Алгоритм использует три набора переменных: r, s и t.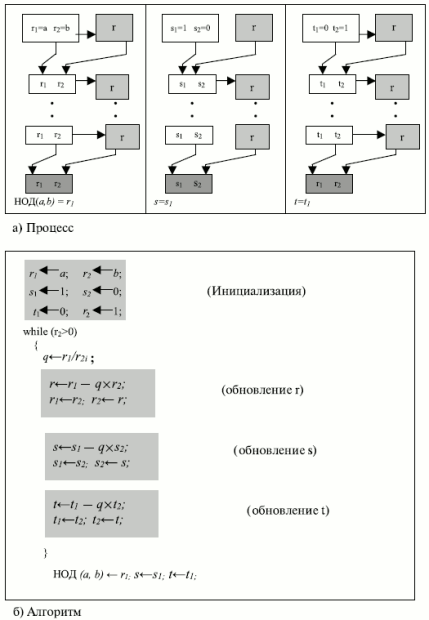




увеличить изображение
Рис. 2.8. Расширенный алгоритм Евклида

На каждом шаге переменные r₁, r₂ и r используются так же, как в алгоритме Евклида. Переменным r₁ и r₂присваиваются начальные значения a и b соответственно. Переменным s₁ и s₂ присваиваются начальные значения 1 и 0соответственно. Переменным t₁ и t₂ присваиваются начальные значения 0 и 1, соответственно. Вычисления r, s и tодинаковы, но с одним отличием. Хотя r — остаток от деления r₁ на r₂, такого соответствия в других двух группах вычислений нет. Есть только одно частное, q, которое вычисляется как r₁/r₂ и используется для других двух вычислений.

Пример 2.9

Дано a = 161 и b = 28, надо найти НОД (a, b) и значения s и t.

Решение

r = r₁ – q x r₂ s = s₁ – qs₂ t = t₁ – q x t₂

Для отображения алгоритма мы используем следующую таблицу:

q	r1	r2	R	s1	s2	s	t1	t2	t
5	161	28	21	1	0	1	0	1	-5
1	28	21	7	0	1	-1	1	-5	6
3	21	7	0	1	-1	4	-5	6	-23
	7	0		-1	4		6	-23

Мы получаем НОД (161, 28) = 7, s = –1 и t = 6. Ответы могут быть проверены, как это показано ниже.

(–1) x 161 + 6 x 28 = 7

Пример 2.10

Дано a = 17 и b = 0, найти НОД (a, b) и значения s и t.

Решение

Для отображения алгоритма мы используем таблицу.

q	r1	r2	R	s1	s2	s	t1	t2	t
	17	0		1	0		0	1

Обратите внимание, что нам не надо вычислять q, r и s. Первое значение r₂ соответствует условию завершения алгоритма. Мы получаем НОД (17, 0) = 17, s = 1 и t = 0. Это показывает, почему мы должны придавать начальные значения s₁ — 1 и t₁ — 0. Ответы могут быть проверены так, как это показано ниже:

(1 x 17) + (0 x 0) = 17

Пример 2.11

Даны a = 0 и b = 45, найти НОД (a, b) и значения s и t.

Решение

Для отображения алгоритма мы используем следующую таблицу:

q	r1	r2	R	s1	s2	s	t1	t2	t
0	0	45	0	1	0	1	0	1	0
	45	0		0	1		0	1

Мы получаем НОД (0,45) = 45, s = 0 и t = 1. Отсюда ясно, что мы должны инициализировать s₂ равным 0, а t₂ — равным 1. Ответ может быть проверен, как это показано ниже:

(0 x 0) + (1 x 45) = 45