Методы решения некорректно поставленных задач. Методы_решения_некорректно_поставленных_задач_-_StudentLib. Рассмотрим систему линейных алгебраических уравнений

• Название: Рассмотрим систему линейных алгебраических уравнений
• Анкор: Методы решения некорректно поставленных задач
• Дата: 13.07.2022
• Размер: 270.5 Kb.
• Имя файла: Методы_решения_некорректно_поставленных_задач_-_StudentLib.com[1.doc
• Тип: Документы; #630246
• страница: 3 из 4

3.МЕТОД РЕГУЛЯРИЗАЦИИ РЕШЕНИЯ ОПЕРАТОРНЫХ УРАВНЕНИЙ

В главе предыдущем разделе рассмотрены случаи, когда класс возможных решений уравнения (2; 0,1) является компактом. Однако для ряда прикладных задач характерна ситуация, когда этот класс F не является компактом, и, кроме того, изме­нения правой части уравнения

Аz= u, (3; 0,1)

связанные с ее приближенным характером, могут выво­дить за пределы множества AF — образа множества F при отображении его с помощью оператора А. Такие задачи называются существенно некорректными. Был разработан новый подход к решению некорректно поставленных задач, позволяющий строить приближенные решения уравнения (3; 0,1), устойчивые к малым изме­нениям исходных данных, для существенно некорректных задач. В основе этого подхода лежит фундаментальное понятие регуляризирующего оператора (P.O.) . Для упрощения изложения в настоящей главе мы будем полагать, что в уравнении (3; 0,1) приближенной может быть лишь пра­вая часть и, а оператор А известен точно.
3.1. Понятие регуляризирующего оператора

3.1.1. Пусть оператор А в уравнении (3; 0,1) таков, что обратный ему оператор

A^-1 не является непрерывным на множестве AF и множество возможных решений F не является компактом.

Пусть z_T есть решение уравнения Az =u_T, т. е. Az_T=u_T. Часто вместо u_T мы имеем некоторый элемент u_ и известное число  > 0 такие, что _U(u_,u_T)<=, т. е. вместо точных исходных данных (u_T,А) мы имеем при­ближенные исходные данные (u_, А) и оценку их погрешности . Задача состоит в том, чтобы по известным исход­ным данным (u_, A, ) найти приближение z_ к элементу z_t, обладающее свойством устойчивости к малым измене­ниям u_. Очевидно, что в качестве приближенного реше­ния z_ уравнения (3; 0,1) нельзя брать точное решение этого уравнения с приближенной правой частью и= u_, т. е. элемент z_T, определяемый по формуле

z_=A^-1 u_

так как оно существует не для всякого элемента uU ине обладает свойством устойчивости к малым изменениям правой части и.

Числовой параметр  характеризует погрешность пра­вой части уравнения (3;0,1). Поэтому представляется естественным определить z_ с помощью оператора, зави­сящего от параметра, значения которого надо брать согла­сованными с погрешностью  исходных данных u_ . Эта согласованность должна быть такой, чтобы при 0, т. е. при приближении (в метрике пространства U) правой части u_ уравнения (3; 0,1) к точному значению u_T, при­ближенное решение z_ стремилось бы (в метрике прост­ранства F) к искомому точному решению z_t уравнения Az_T =u_T.

Пусть элементы z_T  F и u_T U связаны соотношением Az_T = u_T.

Определение 1. Оператор R(и,), действующий из пространства U в пространство F, называется регуля-ризирующим для уравнения Az = и (относительно эле­мента u_T), если он обладает свойствами:

1) существует такое число 1 > 0, что оператор R(u, ) определен для всякого , 0<=<=1, и любого u_U такого, что

_U(u_,u_T)<=;

2) для всякого  > 0 существует 0=0(, u_)<=1 такое, что из неравенства

_U(u_,u_T)<=<=0;

следует неравенство

_F(z_,z_T)<=,

где

z_=R(u_,).

Здесь не предполагается, вообще говоря, однозначность оператора R(u,). Через z_ обозначается произвольный элемент из множества {R(u_,)} значений оператора R(u_,).

3.1.2. В ряде случаев целесообразнее пользоваться другим определением регуляризирующего оператора (P.O.).

Определение 2. Оператор R(u,), зависящий от параметра  и действующий из U в F, называется регуляризирующим для уравнения Az=и (относительно эле­мента u_T), если он обладает свойствами:

1) существуют такие числа 1>0,1>0, что опера­тор R(u,) определен для всякого , принадлежащего промежутку (0,1), и любого uU, для которого

_U(u,u_T)<=1;

2) существует такой функционал =(u,), опреде­ленный на множестве U₁{u;(u,u_T)<=1} эле­ментов иU, что для любого  > 0 найдется число ()<=1 такое, что если u¹U и _U(u¹,u_T)<=<=(), то

_F(z_,z_T)<= , где

z_=R(u¹,(u¹,)).

В этом определении не предполагается однозначность оператора R(u¹,(u¹,)). Следует отметить, что при =  получаем определение 1 .

3.1.3. Если _U(u_,u_T)<=, то известно, что в качест­ве приближенного решения уравнения (3; 0,1) с прибли­женно известной правой частью u_ можно брать элемент z_=R(,), полученный с помощью регуляризирующе­го оператора R(u,), где =(u_)=1() согласовано с погрешностью исходных данных u_. Это решение назы­вается регуляризованным решением уравнения (3; 0,1). Числовой параметр  называется параметром регуляриза­ции. Очевидно, что всякий регуляризирующий оператор вместе с выбором параметра регуляризации , согласо­ванного с погрешностью исходных данных u_ , =(u_), определяет устойчивый к малым изменениям правой час­ти и метод построения приближенных решений уравнения (3;0,1). Если известно, что _U(u_,u_T)<=, то согласно определению регуляризирующего оператора можно так выбрать значение параметра регуляризации =(u_) ,

что при 0 регуляризованное решение R(u_,(u_)) стремится (в метрике F) к искомому точному ре­шению z_T, т. е. _F(z_T,z_(u)). Это и оправдывает пред­ложение брать в качестве приближенного решения урав­нения (3; 0,1) регуляризованное решение.

Таким образом, задача нахождения приближенного решения уравнения (3; 0,1), устойчивого к малым изме­нениям правой части, сводится:

а) к нахождению регуляризирующих операторов;

б) к определению параметра регуляризации  по до­полнительной информации о задаче, например, по величи­не погрешности, с которой задается правая часть u_.

Описанный метод построения приближенных решений называется методом регуляризации.
3.2. О решении вырожденных и плохо обусловленных систем линейных алгебраических уравнений
3.2.1. Известно, с какими трудностями связано решение так называемых плохо обусловленных систем линей­ных алгебраических уравнений: малым изменениям пра­вых частей таких систем могут отвечать большие (выхо­дящие за допустимые пределы) изменения решения.

Рассмотрим систему уравнений

Аz=u, (3; 2,1)

где А — матрица с элементами a_ij, А ={a_ij}, z — иско­мый вектор с координатами z_j , z={z_j}, и — известный вектор с координатами и_i ,u= {u_i}, i, j =1, 2, ..., п.Система (3; 2,1) называется вырожденной, если опреде­литель системы равен нулю, detA = 0. В этом случае матрица А имеет равные нулю собственные значения. У плохо обусловленных систем такого вида матрица А имеет близкие к нулю собственные значения.

Если вычисления производятся с конечной точностью, то в ряде случаев не представляется возможным уста­новить, является ли заданная система уравнений вырож­денной или плохо обусловленной. Таким образом, плохо обусловленные и вырожденные системы могут быть не­различимыми в рамках заданной точности. Очевидно, такая ситуация имеет место в случаях, когда матрица А имеет достаточно близкие к нулю собственные значения.

В практических задачах часто правая часть и и эле­менты матрицы А, т. е. коэффициенты системы (3; 2,1), известны приближенно. В этих случаях вместо системы (3;2,1) мы имеем дело с некоторой другой системой Az=и такой, что ||A-A||<=h, ||u-u||<=, где смысл норм обычно определяется характером задачи. Имея

вместо матрицы А матрицу A, мы тем более не можем высказать определенного суждения о вырожденности или невырожденности системы (3; 2,1).

В этих случаях о точной системе Аz=u, решение которой надо определить, нам известно лишь то, что для матрицы А и правой части и выполняются неравенства

||A-A||<=h, ||u-u||<=. Но систем с такими исходными данными (А, и) бесконечно много, и в рамках извест­ного нам уровня погрешности они неразличимы. Поскольку вместо точной системы (3; 2,1) мы имеем приближенную систему Аz= и, то речь может идти лишь о нахождении приближенного решения. Но приближенная система Аz=и может быть неразрешимой. Возникает вопрос:

что надо понимать под приближенным решением систе­мы (3; 2,1) в описанной ситуации?

Среди «возможных точных систем» могут быть и вы­рожденные. Если они разрешимы, то имеют бесконечно много решений. О приближенном нахождении какого из них должна идти речь?

Таким образом, в большом числе случаев мы должны рассматривать целый класс неразличимых между собой (в рамках заданного уровня погрешности) систем урав­нений, среди которых могут быть и вырожденные, и неразрешимые. Методы построения приближенных реше­ний систем этого класса должны быть одними и теми же, общими. Эти решения должны быть устойчивыми к малым изменениям исходных данных (3; 2,1).

В основе построения таких методов лежит идея «от­бора». Отбор можно осуществлять с помощью специальных, заранее задаваемых функционалов [ z ] , входящих в постановку задачи.

Неотрицательный функционал [ z ] , определенный на всюду плотном в F подмножестве F₁ множества F, называется стабилизирующим функционалом, если:

а) элемент z_T принадлежит его области определения;

б) для всякого числа d>0 множество F_1,d элементов z из F₁ , для которых

[ z ]<=d, компактно на F.

3.2.2. Итак, рассмотрим произвольную систему линейных алгебраических уравнений (короче — СЛАУ)

Аz =u, (3; 2,2)

в которой z и u—векторы, z=(z₁, z₂, ...,z_n)Rⁿ, и=(u₁,u₂, ...,u_n)R^m, А—матрица с элементами a_ij, А = {a_ij}, где j =1, 2, ..., n; i= 1, 2, ..., т, и число п не обязано быть равным числу т.

Эта система может быть однозначно разрешимой, вы­рожденной (и иметь бесконечно много решений) и не­разрешимой.

Псевдорешением системы (3; 2,2) называют вектор z, минимизирующий невязку || Az – u || на всем пространстве Rⁿ. Система (3; 2,2) может иметь не одно псевдоре­шение. Пусть F_A есть совокупность всех ее псевдореше­ний и z¹ — некоторый фиксированный вектор из Rⁿ, оп­ределяемый обычно постановкой задачи.

Нормальным относительно вектора z¹ решением си­стемы (3;2,2) будем называть псевдорешение z⁰ с ми­нимальной нормой || z – z¹ ||, т. е. такое, что

|| z⁰ – z¹ || =
Здесь 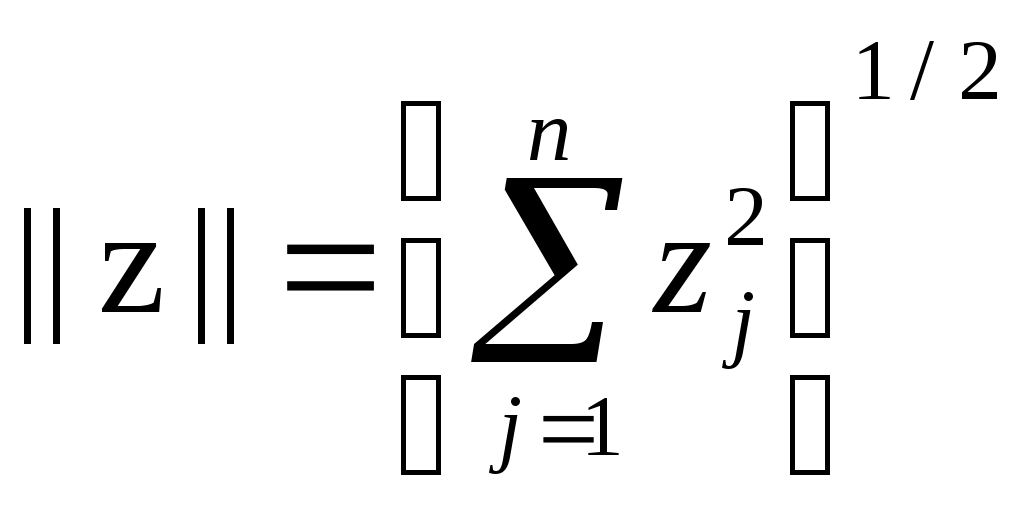. В дальнейшем для простоты записи будем считать z¹= 0 и нормальное относительно вектора z¹=0 решение называть просто нормальным ре­шением.

Для любой системы вида (3; 2,2) нормальное решение существует и единст­венно.

Замечание 1. Нормальное решение z° системы (3;2,2) можно определить также как псевдорешение, минимизирующее заданную положительно определенную квадратичную форму относительно координат вектора z—z¹. Все излагаемые ниже результаты остаются при этом справедливыми.

Замечание 2. Пусть ранг матрицы А вырожден­ной системы (3; 2,1) равен r < n и z_r+1,z_r+2, … , z_n— базис линейного пространства N_A, состоящего из элемен­тов z, для которых Аz=0, N_A = {z; Аz= 0}. Решение z° системы (3; 2,1), удовлетворяющее n—r условиям ортогональности

(z⁰ – z¹, z_S)= 0, S= r + 1, r + 2, .. ,n, (3; 2,3)

определяется однозначно и совпадает с нормальным ре­шением.

3.2.3. Нетрудно видеть, что задача нахождения нормаль­ного решения системы (3; 2,2) является некорректно поставленной. В самом деле, пусть А — симметричная матрица. Если она невырожденная, то ортогональным преобразованием

z = Vz*, u = Vu*

ее можно привести к диагональному виду и преобразо­ванная система будет иметь вид

_iz_i*=u_i* , i= 1, 2,. .., п,

где _i — собственные значения матрицы А.

Если симметричная матрица А — невырожденная и имеет ранг r, то n – r ее собственных значений равны нулю. Пусть

_i0 для i=1, 2, ..., r;

и

_i=0 для i=r+1,r+2, …, n.

Полагаем, что система (3; 2,2) разрешима. При этом u_i*= 0 для i =r + 1, ..., n.

Пусть «исходные данные» системы (А и и) заданы с погрешностью, т. е. вместо А и и заданы их прибли­жения А и u:

|| A – A ||<=h, ||u – u||<= . При этом

(3;2,4)

Пусть _i — собственные значения матрицы А. Извест­но, что они непрерывно зависят от А в норме (3; 2,4). Следовательно, собственные значения _r+1 , _r+2, …,_nмогут быть сколь угодно малыми при достаточно малом h.

Если они не равны нулю, то
z_i*= .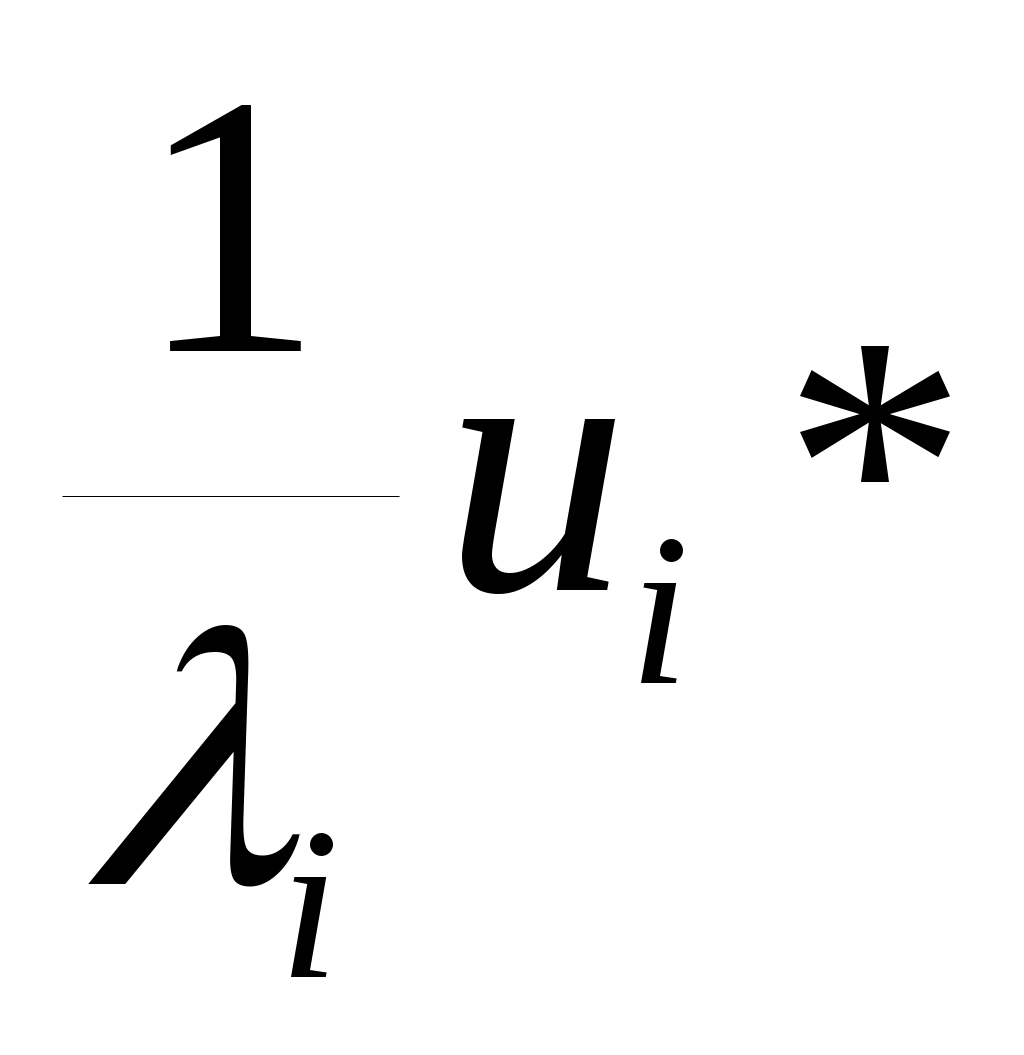

Таким образом, найдутся возмущения системы в пре­делах любой достаточно малой погрешности А и и, для которых некоторые z_i* будут принимать любые наперед заданные значения. Это означает, что задача нахожде­ния нормального решения системы (3; 2,2) является неустойчивой.

Ниже дается описание метода нахождения нормального решения системы (3; 2,2), устойчивого к малым (в норме (3; 2,4)) возму­щениям правой части и , основанного на методе регуляризации.
3.3. Метод регуляризации нахождения нормального решения
3.3.1. Пусть z° есть нормальное решение системы

Аz = и. (3; 3,1)

Для простоты будем полагать, что прибли­женной может быть лишь правая часть, а оператор (матрица) А — точный.

Итак, пусть вместо и мы имеем вектор и, || и — и || <=; т. е. вместо системы (3;3,1) имеем систему


(3; 3,2)


Аz = u.




Требуется найти приближение z_ к нормальному реше­нию системы (3;3,1), т. е. к вектору z° такое, что z_ z° при  0. Отметим, что векторы u и u (один из них или оба) могут не удовлетворять классическому ус­ловию разрешимости.

Поскольку система (3; 3,1) может быть неразреши­мой, то inf ||Az-u|| =  >=0, где inf берется по всем векторам z  Rⁿ.

Естественно искать приближения z_ в классе Q_ век­торов z, сопоставимых по точности с исходными данны­ми, т. е. таких, что || Az – u ||<=+. Но поскольку вместо вектора u мы имеем вектор u, то мы можем найти лишь

=inf || Az – u ||.

z Rⁿ

Отметим, что из очевидных неравенств

||Az – u ||<=||Az – u || + || u – u || ,

||Az – u ||<= || Az – u || + ||u – u ||

следуют оценки <=+, <=+, приводящие к не­равенству |  —  | <=. Поэтому будем искать прибли­жение z_ к нормальному решению z° в классе Q_ векто­ров z, для которых || Аz — и || <= +2. Отметим, что если имеется информация о разрешимости системы (3;3,1), то  = 0 и в качестве класса Q_ можно брать класс векторов z, для которых || Аz — и|| <= . Класс Q_ есть класс формально возможных приближенных решений.

Но нельзя в качестве z_ брать произвольный вектор из класса Q_, так как такое «приближение» будет неустойчивым к малым изменениям правой части уравнения (3;3,2). Необходим принцип отбора. Он естественным образом вытекает из постановки задачи. В самом деле согласно определению нормального решения искомое ре­шение z° должно быть псевдорешением с минимальной нормой. Поэтому в качестве приближения к z° естествен­но брать вектор z_ из Q_, минимизирующий функционал

[ z ] = ||z||² на множестве Q_ .

Таким образом, задача сводится к минимизации функ­ционала [ z ] = ||z||² на множестве Q_ векторов z, для которых выполняется условие || Аz — u || <= +2.

3.3.2. Пусть z_ — вектор из Q_, на котором функционал ||z||² достигает минимума на множестве Q_. Его можно рассматривать как результат применения к правой части u уравнения (3; 3,2) некоторого оператора R₁(u,), зависящего от параметра . Справедлива

Теорема 1. Оператор R₁(u,) обладает следующи­ми свойствами:

1) он определен для всякого uR^m и любого  > 0;

2) при  0 z_== R₁(u,) стремится к нормальному решению z° уравнения Аz=u, т. е. он является регуляризирующим для уравнения Аz=u .

3.3.3. Пусть z_ — вектор, на котором функционал [ z ] = ||z||² достигает минимума на множестве Q_. Легко ви­деть из наглядных геометрических представлений, что вектор z_ лежит на границе множества Q_, т.е. ||Az_ - u ||= +2=₁.
Это следует непосредственно также из того, что функционал [ z ] = ||z||² является сстабилизирующим и квазимонотонным. Стабилизирующий функционал [ z ] называется квазимонотонным , если каков бы ни был элемент z из F₁ , не принадлежащий множеству M₀ , в любой его окрестности найдется элемент z₁ из F₁, для которого [ z₁ ]<[ z ], т.е. если функционал не имеет локальных минимумов на множестве F₁\ M₀.
Задачу нахождения вектора z_ можно поставить так: среди векторов z, удовлетворяющих условию ||Az – u ||= +2, найти вектор z_ с минимальной нормой, т. е. минимизирующий функционал [ z ]=||z||².

Последнюю задачу можно решать методом Лагранжа, т. е. в качестве z_ брать вектор z^, минимизирующий функционал

М^ [z, u] = ||Az - u ||²+||z||², >0,

с параметром , определяемым по невязке, т. е. из ус­ловия ||Аz^— u||=1. При этом параметр  определяется однозначно .

3.3.4. Поскольку М^ [z, u] — квадратичный функционал, то для любых uR^m и > 0 существует лишь один минимизирующий его вектор z^. В самом деле, допустим,

что существуют два вектора z^ и z^, минимизирующие его. Рассмотрим векторы z, расположенные на прямой (пространства Rⁿ), соединяющей z^ и z^:

z = z^ + (z^ - z^).

Функционал М^ [z, u] на элементах этой прямой есть неотрицательная квадратичная функция от . Следова­тельно, она не может достигать наименьшего значения при двух различных значениях :  = 0 (z = z^) и =1 (z = z^).

Компоненты z_j^ вектора z^ являются решением си­стемы линейных алгебраических уравнений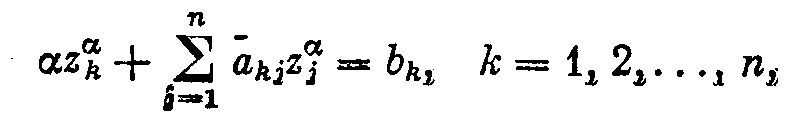



получающихся из условий минимума функционала М^ [z, u]:



Здесь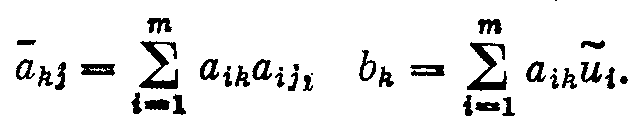


Компоненты z_j^ могут быть определены и с помощью какого-нибудь другого алгоритма минимизации функцио­нала М^ [z, u].

Вектор z^ можно рассматривать как результат приме­нения к u некоторого оператора z^=R(u, ), завися­щего от параметра .

Покажем, что оператор R₀(u, ) является регуляризирующим для системы (3;3,1), т. е. обладает свойствами 1) и 2) определения 2 (см. 3.1.2.). В п. 3.3.2. было сказано, что он определен для всяких uR^m и  > О и, следовательно, обладает свойством 1). Теперь пока­жем справедливость свойства 2), т. е. существование таких функций = , что векторы z^ = R₀(u, ) сходятся к нормальному решению z° системы (3; 3,1) при 0. Это непосредственно следует из приводимой ниже теоремы 2.

Теорема 2( Тихонова). Пусть z° есть нормальное решение си­стемы Az= u и вместо вектора u мы имеем вектор u такой, что ||u—u||<=. Пусть, далее,  и  — какие-либо непрерывные на [0, 2] и положительные на (02] функции, монотонно стремящиеся к нулю при  0 и такие, что



Тогда для любой .положительной на (0, ] функции  , удовлетворяющей условиям



векторы z^ = R₀(u, ) сходятся к нормальному ре­шению z⁰ системы Az = u при 0, т. е.



Примечание. Доказательства теорем в данном разделе опущены, т.к. основной теоретической частью работы является раздел «Метод Подбора. Квазирешения». Метод Тихонова описан из-за использования его в численном эксперименте.

ЗАКЛЮЧЕНИЕ
Для реализации численного примера был выбран метод Тихонова решения плохо обусловленных СЛАУ. В качестве исходной была взята СЛАУ Az=u, имеющая в матричной записи вид: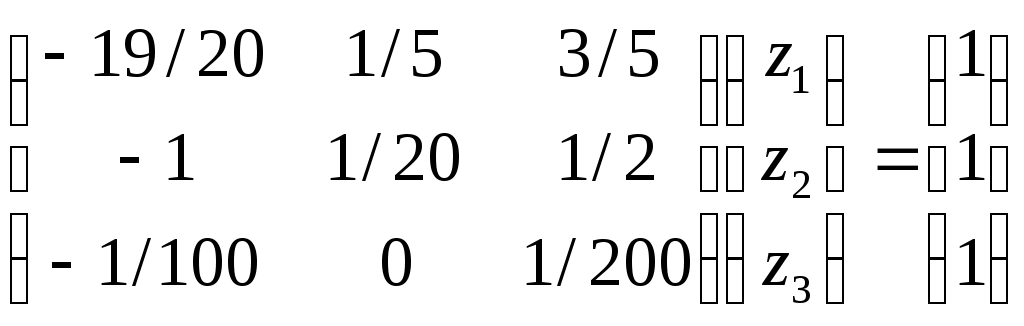



Определитель матрицы коэффициентов этой системы близок к нулю – он равен 0.000125. Попробуем решить эту систему с помощью обратной матрицы:

z=A^-1u

Получим z₁=316

z₂=-990

z₃=832

Теперь предположим, что правая часть нам известна приближенно, с погрешностью 0.1 Изменим, к примеру, третий элемент вектора-столбца с 1 на 1.1 :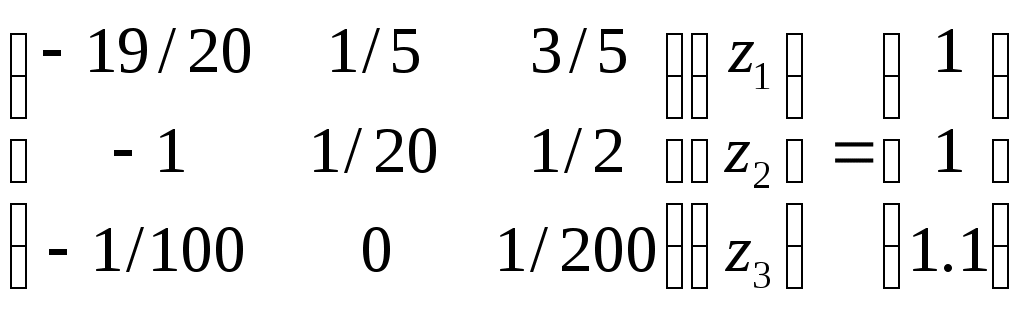



Попробуем решить новую систему также с помощью обратного оператора. Мы получаем другой результат:

z₁=348

z₂=-1090

z₃=916.

Мы видим, что малому изменению правой части данной системы отвечают весьма значительные изменения решения. Очевидно, эта система – плохо обусловленная, и здесь не может идти речи о нахождении решения близкого к точному с помощью обратного оператора.

Будем искать решение методом Тихонова. В теоретической части было показано, что целесообразно использовать регуляризирующий оператор следующего вида: (E + A^TA)z^=A^Tu_ , где E – единичная матрица, z^приближенное нормальное решение, A^T – транспонированная исходная матрица, параметр регуляризации,

u_ -- правая часть, заданная неточно. Эту задачу можно решать стандартными методами, задав предварительно функцию удовлетворяющую условиям теоремы Тихонова. В моем примере это функция =/4^Далее будем решать регуляризованную задачу с точностью .001 ,последовательно изменяя значения .

В качестве контр-примера можно подставить в программу любую функцию  , не удовлетворяющую условиям теоремы Тихонова. Любая положительная функция монотонно возрастающая, не обладающая свойством 0 при 0, не будет минимизировать невязку.

Текст программы приведен в приложении 1. Полная распечатка результатов приведена в приложении 2. Здесь же представлены окончательные значения на выходе из программы.
Приближение к нормальному решению

Z(1)= 3.47834819174013E+0002

Z(2)=-1.08948394975175E+0003

Z(3)= 9.15566443137791E+0002
Значение правой части при подстановке прибл. решения

U1(1)= 9.99997717012495E-0001

U1(2)= 1.00000741970775E+0000

U1(3)= 1.09948402394883E+0000
Значение параметра регуляризации:

2.61934474110603E-0010