Методы решения некорректно поставленных задач. Методы_решения_некорректно_поставленных_задач_-_StudentLib. Рассмотрим систему линейных алгебраических уравнений
 Скачать 270.5 Kb. Скачать 270.5 Kb.
|
|
2.2. Квазирешения 2.2.1. Пусть оператор А в уравнении (2; 0,1) — вполне непрерывный. Построение устойчивого к малым изменениям правой части и приближенного решения уравнения (2; 0,1) по формуле z=A-1u (2; 2,1) возможно в тех случаях, как отмечалось в 2.1. , когда решение ищется на компакте МF и правая часть уравнения принадлежит множеству N = AM. Обычно не существует эффективных критериев, позволяющих установить принадлежность элемента и множеству N. Это приходится предполагать известным априори. В практических задачах часто вместо точного значения правой части иT нам известно ее приближенное значение u1, которое может не принадлежать множеству N=AM. В этих случаях нельзя строить приближенное решение уравнения (2; 0,1) по формуле (2; 2,1), так как символ А-1u может не иметь смысла. 2.2.2. Стремление устранить затруднения, связанные с отсутствием решения уравнения (2; 0,1) при неточной правой части, привело В. К. Иванова к понятию квазирешения уравнения (2; 0,1) — обобщению понятия решения этого уравнения. Элемент z1М, минимизирующий при данном и функционал U(Az1,и) на множестве М, называется квазирешением уравнения (2; 0,1) на М, 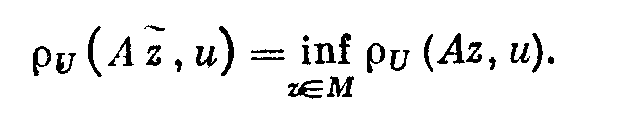 Если М — компакт, то квазирешение, очевидно, существует для любого иU и если, кроме того, иAM, то квазирешение z1 совпадает с обычным (точным) решением уравнения (2; 0,1). Квазирешение может быть и не одно. В этом случае под квазирешенпем будем разуметь любой элемент из множества квазирешений D. Можно указать достаточные условия, при которых квазирешение единственно и непрерывно зависит от правой части и. Напомним определение. Пусть элемент у и множество Q принадлежат пространству U. Элемент q множества Q называется проекцией элемента у на множество Q, q=Ру, если выполняется равенство где 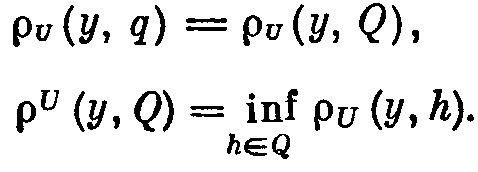 Теорема 1.Если уравнение Аz=u может иметь на компакте М не более одного решения и проекция каждого элемента uU на множество N = AM единственна, то квазирешение уравнения (2; 0,1) единственно и непрерывно зависит от правой части u. Доказательство. Пусть z1 — квазирешение и и1=Аz1. Очевидно, и1 есть проекция элемента u на множество N = AM. По условию теоремы она определяется однозначно. Отсюда, в силу взаимной однозначности отображения множества М на множество N, следует единственность квазирешения z1. Очевидно, что z1 = А-1u=А-1Ри. Согласно лемме о непрерывности обратного отображения компакта (см. предыдущий параграф) оператор А-1 непрерывен на N. Оператор проектирования Р непрерывен на U. Поэтому А-1P— непрерывный на U оператор и, следовательно, квазирешение z1 непрерывно зависит от правой части и. Таким образом, при переходе к квазирешению восстанавливаются все условия корректности, т. е. задача нахождения квазирешения уравнения (2; 0,1) на компакте М является корректно поставленной. Если условие единственности решения уравнения (2; 0,1) не выполнено, то квазирешения образуют некоторое множество D элементов компакта М. В этом случае без упомянутых в теореме 1 ограничений на множество N имеет место непрерывная зависимость множества квазирешений D от и в смысле непрерывности многозначных отображений. Для случая, когда уравнение (2; 0,1) линейно, легко получить более общие результаты, содержащиеся в следующей теореме . Теорема 2. Пусть уравнение (2; 0,1) линейно, однородное уравнение Az=0 имеет только нулевое решение, множество М выпукло, а всякая сфера в пространстве U строго выпукла. Тогда квазирешение уравнения (2; 0,1) на компакте М единственно и непрерывно зависит от правой части и. Доказательство. Пусть z1 — квазирешение и u1=Az1. Так как множество М выпукло, то в силу линейности оператора А множество N=AM также выпукло. Очевидно, что и1 есть проекция элемента и на множество N. В силу того, что сфера в пространстве U по условию теоремы строго выпукла, проекция и определяется однозначно. Далее доказательство завершается, как в теореме 1. 2.2.3. Пусть F и U — гильбертовы пространства, МSR — шар (|| z ||<=R ) в пространстве F и А — вполне непрерывный линейный оператор. В этом случае квазирешение уравнения (2; 0,1) можно представить в виде ряда по собственным элементам (функциям, векторам) n оператора А*А, где А* — оператор, сопряженный оператору А. Известно, что А*А — самосопряженный положительный вполне непрерывный оператор из F в F. Пусть 1>=2>=…>=n>=… — полная система его собственных значений, a 1,2,…,n,…—отвечающая им полная ортонормированная система его собственных элементов (функций, векторов). Элемент А*и можно представить в виде ряда 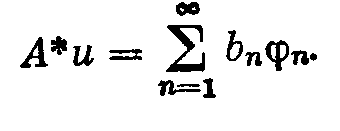 (2;2,2) (2;2,2)В этих условиях справедлива Теорема 3.Квазирешение уравнения (2, 0,1) на множестве SR выражается формулами: 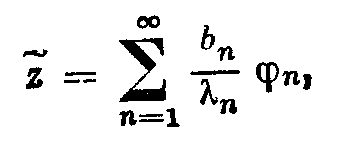 (2;2,3) (2;2,3)если 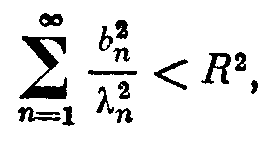 (2;2,4) (2;2,4)и 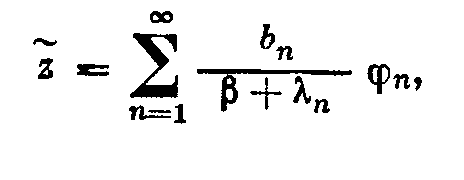 если 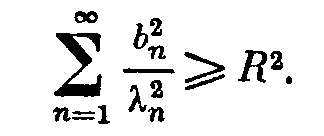 (2;2,5) (2;2,5)Здесь — корень уравнения 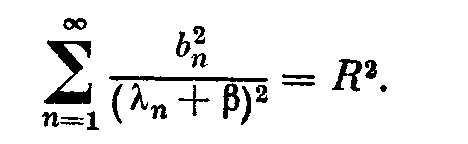 (2;2,6) (2;2,6) Доказательство. Квазирсшение минимизирует функционал U2 (Az, u) == (Az — u, Az — u) (2;2,7) (где (v,w ) — скалярное произведение элементов v и w из U), уравнение Эйлера для которого имеет вид A*Az=A*u. (2;2,8) Решение этого уравнения будем искать в виде ряда по системе {n}: 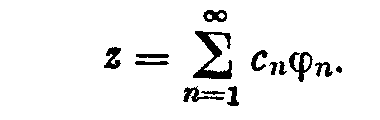 (2;2,9) (2;2,9) Подставляя этот ряд в уравнение (2; 2,8) и используя разложение (2;2,2), находим сn=bn/n. Следовательно, неравенство (2; 2,4) означает, что ||z|| Если же выполняется неравенство (2; 2,5), то это означает, что ||z||>=R и надо решать задачу на условные экстремум функционала (2; 2,7) при условии, что || z ||2 = R2. Методом неопределенных множителей Лагранжа эта задача сводится к нахождению безусловного экстремума функционала (Аz-u, Аz-u) + (z, z), а последняя — к решению отвечающего ему уравнения Эйлера A*Az+z=А*и. Подставляя сюда z в виде ряда (2; 2,9) и используя разложение (2; 2,2), находим Параметр определяем из условия || z ||2 = R2 , которое эквивалентно (2; 2,6). 2.3. Приближенное нахождение квазирешений В предыдущем параграфе мы видели, что нахождение квазирешения связано с нахождением элемента в бесконечномерном пространстве. Для приближенного нахождения квазирешения естественно переходить к конечномерному пространству. Можно указать достаточно общий подход к приближенному нахождению квазирешений уравнения (2; 0,1) , в котором А—вполне непрерывный оператор. Будем полагать, что выполнены указанные в 2.2. достаточные условия существования единственного квазирешения на заданном множестве М, т. е. полагаем, что множество М — выпуклый компакт и сфера в пространстве U строго выпукла. Пусть M1 MMn — возрастающая цепочка компактных замкнутых множеств Мn такая, что замыкание их объединения Покажем, что в качестве приближения к квазирешению z1 на множестве М можно брать любой элемент z1n из Тn . При этом Пусть Nn = АМn и Вn — множество проекций элемента и на множество Nn . Очевидно, что Вn = АТn и N1 N2 … Nn; тогда U(u,N1)>= …>= U (u,Nn)>=… U (u,N)= U (u,Az1) .(2;3,1) Так как множество U(u,Nn)<U(u,N)+ (2; 3,2) Из (2; 3,1) и (2; 3,2) следует, что Поскольку то 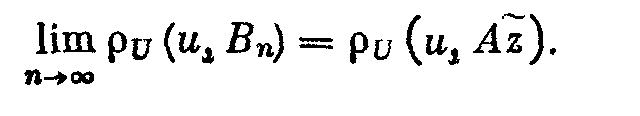 (2;3,4) Каждое множество Вn есть компакт, так как оно является замкнутым подмножеством компакта Nn. Поэтому в Вnнайдется такой элемент уn , что U(yn ,u) = inf U(y,u) yBn Последовательность {yn} имеет хотя бы одну предельную точку, принадлежащую N, так как N — компакт. Пусть у0 — какая-нибудь предельная точка множества {yn} и {уnk} — подпоследовательность, сходящаяся к y0 , т. е. Из (2; 3,3) и (2; 3,4) следует, что 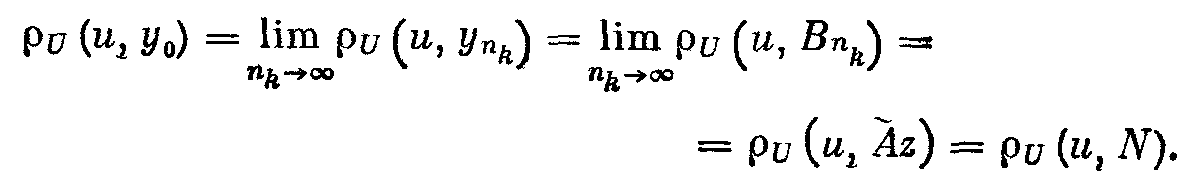 Таким образом, U(u,y0)=U(u,N). Отсюда и из единственности квазирешения на множестве М следует, что y0=Az1. Так как у0 — произвольная предельная точка множества {yn}, то последовательность {уn} сходится к Аz1. Это и означает, что в качестве приближения к квазирешению можно брать любой элемент z1n из множества Тп , так как в силу леммы параграфа 2.1. z1nz* при n. Если в качестве Мп брать конечномерные (n-мерные) множества, то задача нахождения приближенного квазирешения на компакте М сводится к минимизации функционала U(Az, u) на множестве Мп, т. е. к нахождению минимума функции п переменных. 2.4. Замена уравнения Аz=u близким ему Уравнения вида (2; 0,1), в которых правая часть u не принадлежит множеству N=AM, изучались М. М. Лаврентьевым . Ему принадлежит идея замены исходного уравнения (2; 0,1) близким ему, в некотором смысле, уравнением, для которого задача нахождения решения устойчива к малым изменениям правой части и разрешима для любой правой части uU. В простейшем случае это делается следующим образом. Пусть FUН — гильбертовы пространства, А — линейный, ограниченный, положительный и самосопряженный оператор, SR {х, ||x||<=R, xF} есть шар радиуса R в пространстве F, В — вполне непрерывный оператор, определенный на SR при любом R > 0. В качестве класса корректности М берется множество DR=BSR — образ шара SR при отображении с помощью оператора В. Предполагается, что искомое точное решение zT уравнения (2; 0,1) с правой частью u=uT существует и принадлежит множеству DR. Уравнение (2; 0,1) заменяется уравнением (A+E)z Az+z=u , (2:4,1) где >0 – числовой параметр. Решение уравнения z=(A+E)-1u , (2; 4,2) при соответствующем выборе параметра , принимается за приближенное решение уравнения (2; 0,1). Здесь Е — единичный оператор. Замечание. Для оценки уклонения F(zT,z) приближенного решения от точного можно использовать модуль непрерывности обратного оператора на N. Пусть u1, u2 N и U(u1,u2)<=. Тогда (,N)= sup F(A-1u1,A-1u2). u1,u2 N Очевидно, что если U(uT,u)<= и z=A-1u , то F(zT,z)<=(,N). Вернемся к уравнению (2; 4,1). Если || Az ||<= и (,DR) = sup || z ||, то легко DR получить оценку уклонения z от zT. Очевидно, что || z - zT ||<=||z1 - zT|| + ||z - z1||, (2;4,3) где z1=(A + E)-1uT. Следовательно, ||z - zT||<=(,DR) + /. (2;4,4) Если известен модуль непрерывности (,DR) или его мажоранта, то из (2; 4,4) можно найти значение параметра как функцию , при котором правая часть в неравенстве (2; 4,4) будет минимальной. 2. 5. Метод квазиобращения 2.5.1. Известно, что задача Коши для уравнения теплопроводности с обратным течением времени является неустойчивой к малым изменениям начальных значений. Неустойчивость сохраняется и в случаях, когда решение подчиняется некоторым дополнительным граничным условиям. Для устойчивого решения таких задач разработан метод квазиобращения . Мы изложим существо его для простейшего уравнения теплопроводности, не вдаваясь в вопросы обоснования. Подробное изложение в применении к более широкому классу задач содержится в . 2.5.2. Рассмотрим прямую задачу. Пусть D — конечная область n-мерного евклидова пространства Rn точек x = (x1, x2, ...,xn), ограниченная кусочно-гладкой поверхностью S, a t — время. Пусть, далее, (x) — заданная непрерывная в D функция. Прямая задача состоит в нахождении решения u=u(x,t) уравнения в области G {x D, t > 0}, удовлетворяющего граничным условиям u(х, t) =0 при xS(2; 5,2) и начальным условиям u(x, 0)=(x). (2; 5,3) Здесь 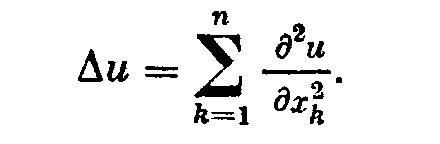 Известно, что решение такой задачи существует. Каждой функции (x)C отвечает решение задачи (2; 5,1)— (2; 5,3). Будем обозначать его через u(х, t;). Обратная задача состоит в нахождении функции (х)по известной функции u(х,t;). В реальных задачах функция u(x,t;) обычно получается в результате измерений и, следовательно, известна приближенно. Будем полагать, что uL2. Такая функция может и не соответствовать никакой «начальной» функции (х). Таким образом, может не существовать в классе функций С решения обратной задачи. Поэтому будем рассматривать задачу нахождения некоторого обобщенного решения обратной задачи. Пусть заданы число T > 0 и функция (x), определенная в области D,(x)L2. На функциях (х) класса С определен функционал 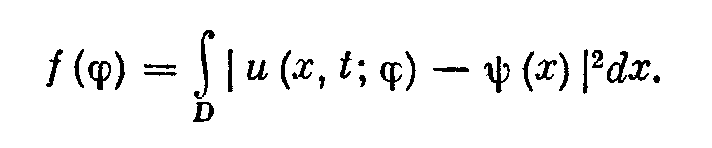 Обобщенным решением обратной задачи будем называть функцию (х)., на которой достигается f0=inf f() C Замечание. «Естественный» подход к решению этой задачи — выбрать функцию (х).так, чтобы f()=0 . Для этого достаточно найти решение прямой задачи u(x, t) = 0 для х S, 0 < t < T; u(x,T) = (x) и положить (x) = u(x,0). Но такая задача при заданной функции (x) из L2, вообще говоря, неразрешима и, кроме того, неустойчива к малым изменениям функции (x). На некотором классе обобщенных функций (x) f0=0 . Поэтому рассматривается задача нахождения приближенного значения f0 с заданным уровнем погрешности. Для заданного числа > 0 найти функцию (x), на которой f ()<=. Эта задача и решается методом квазиобращения. Идея метода квазиобращения состоит в том, что вместо оператора теплопроводности Bu = 0, x D, t < Т, > 0; u (x,T)=(x); u (x,t) = 0 для x S, t< Т устойчива. Решив эту задачу, полагают (x)=u(x,0). Обычно в качестве оператора В берут оператор x D, t u (x,T)=(x); u (x,t) = 0 для x S, 0< t<= Т u=0 для x S, 0< t<= Т. Затем полагают (x)=u(x,0). Следует отметить, что uне сходится в обычном смысле при . |
