РГЗ по мтаематике. РГЗ по математике. Рассмотрим уравнение кривой
 Скачать 454.25 Kb. Скачать 454.25 Kb.
|
 Решение 1) Рассмотрим уравнение кривой 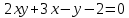 Матрица квадратичной части многочлена второй степени имеет вид 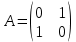 Найдем собственные числа данной матрицы, приравняв определитель матрицы 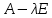 к нулю. Находим матрицу к нулю. Находим матрицу 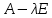 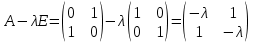 Находим определитель 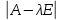 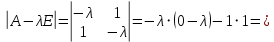 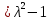 Приравниваем его к нулю и находим собственные числа 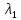 и и 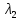 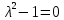 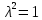 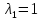 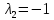 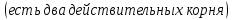 Собственные числа найдены. Находим собственные вектора. Собственный вектор для собственного числа 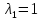 найдем из системы найдем из системы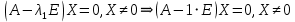 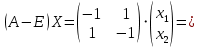 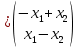 Решим однородную систему уравнений 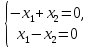 Вычислим ранг матрицы коэффициентов 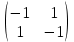 методом окаймляющих миноров. Проверяем, отличен ли от нуля единственный минор второго порядка методом окаймляющих миноров. Проверяем, отличен ли от нуля единственный минор второго порядка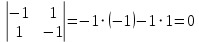 Значит, ранг матрицы коэффициентов равен одному. Выберем в качестве базисного минор элемента первой строки и второго столбца 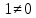 . Тогда, полагая . Тогда, полагая 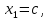 получаем получаем 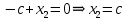 Здесь 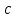 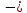 постоянная. Таким образом, общее решение системы постоянная. Таким образом, общее решение системы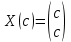 Из общего решения системы находим фундаментальную систему решений 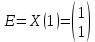 Соответствующий ортонормированный собственный вектор 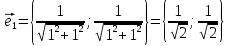 Собственный вектор для собственного числа 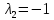 найдем из системы найдем из системы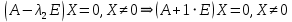 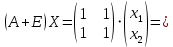 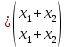 Решим однородную систему уравнений 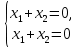 Так как строки матрицы коэффициентов 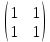 пропорциональны, то ее ранг не может быть больше одного. Значит, ранг матрицы коэффициентов равен одному. Выберем в качестве базисного минор элемента первой строки и первого столбца пропорциональны, то ее ранг не может быть больше одного. Значит, ранг матрицы коэффициентов равен одному. Выберем в качестве базисного минор элемента первой строки и первого столбца 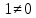 . Тогда, полагая . Тогда, полагая 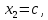 получаем получаем 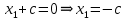 Таким образом, общее решение системы 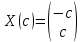 Из общего решения системы находим фундаментальную систему решений 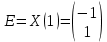 Соответствующий ортонормированный собственный вектор 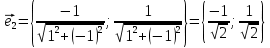 Таким образом мы нашли ортонормированные собственные вектора 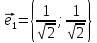 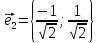 Выберем орты 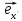 и и 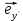 новой системы координат новой системы координат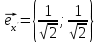 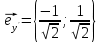 Матрица перехода к новому базису имеет вид 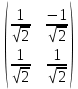 Выполняя преобразование 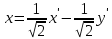 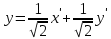 получим 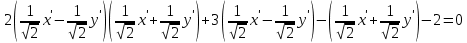 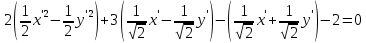 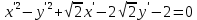 Выделим полные квадраты по переменным 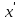 и и 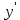 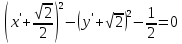 Выполним параллельный перенос системы координат согласно формулам 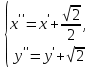 Здесь 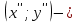 координаты в канонической системе координат, координаты в канонической системе координат, 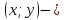 координаты в исходной системе координат. координаты в исходной системе координат. Уравнение кривой принимает вид 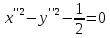 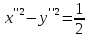 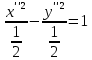 Данное уравнение представляет собой каноническое уравнение гиперболы с полуосями 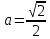 (действительная полуось) и (действительная полуось) и 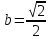 (мнимая полуось). (мнимая полуось).Итоговое преобразование координат 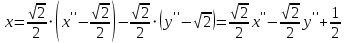 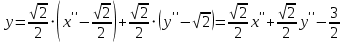 Таким образом, формула преобразования координат 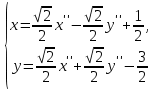 Уравнение Оси 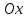 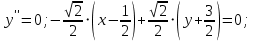 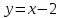 Уравнение оси 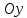 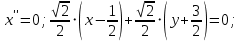 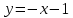 Найдем координаты начала канонической системы координат 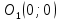 в исходной системе координат. в исходной системе координат.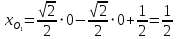 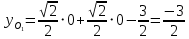 Таким образом, начало канонической системы координат 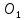 в исходной системе координат имеет координаты в исходной системе координат имеет координаты 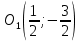 . .Выполним построение 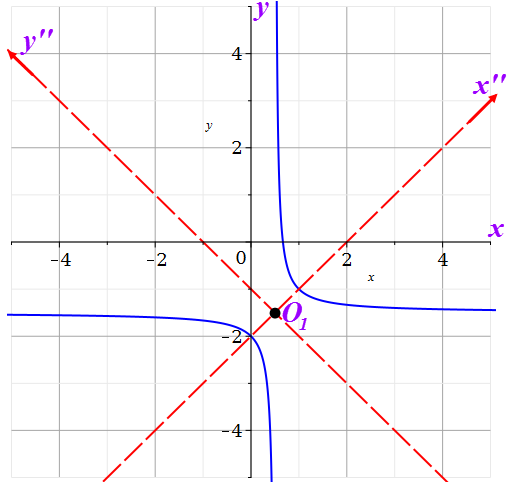 2. Преобразуем 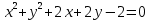 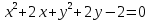 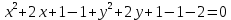 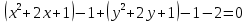 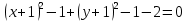 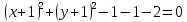 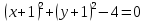 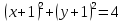 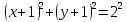 При параллельном переносе координат 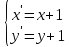 получим кривую 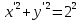 Это каноническое уравнение окружности с центром в начале новой системы координат и радиусом 2. Центр новой (канонической) системы координат в старой системе имеет координаты 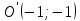 А оси канонической системы координат сонаправлены с осями исходной системы координат. Выполним построение 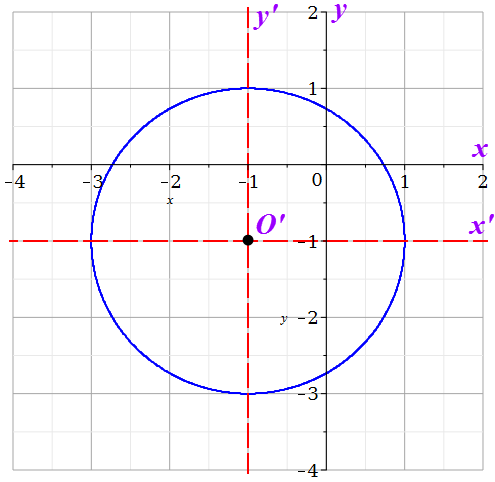 3. Преобразуем 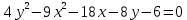 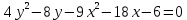 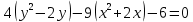 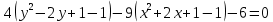 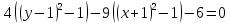 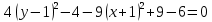 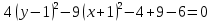 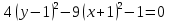 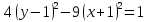 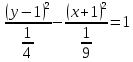 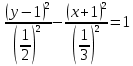 Выполним параллельный перенос системы координат 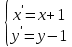 Тогда в новой системе координат кривая примет вид 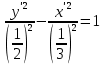 Это каноническое уравнение гиперболы с центром симметрии в начале новой (канонической) системы координат. Полуоси гиперболы равны: действительная полуось 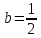 мнимая полуось 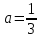 Осью симметрии гиперболы является прямая 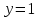 Центр канонической системы координат совпадает с центром симметрии гиперболы и в исходной системе имеет координаты 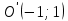 Оси новой системы координат сонаправлены с осями исходной системы. Выполним построение 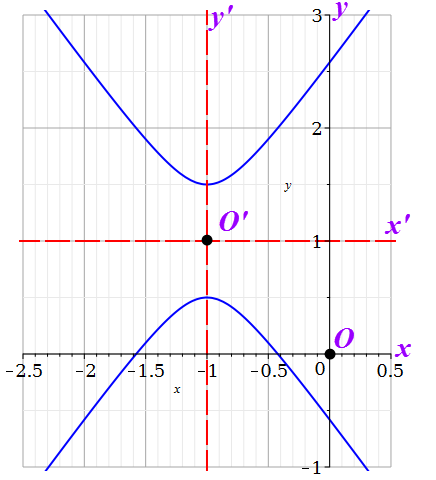 4. Преобразуем 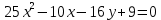 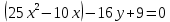 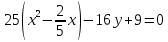 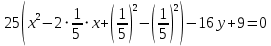 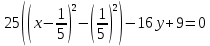 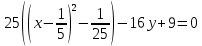 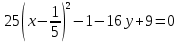 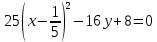 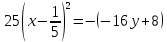 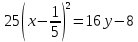 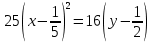 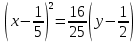 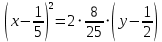 Выполним параллельный перенос по формулам 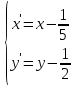 Кривая примет вид 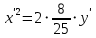 В новой системе координат это каноническое уравнение параболы с осью симметрии осью 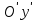 и параметром и параметром 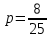 . .Вершина параболы лежит в начале канонической системы координат, в исходной системе имеет координаты 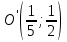 Оси новой (канонической) системы координат сонаправлены с осями исходной. Выполним построение 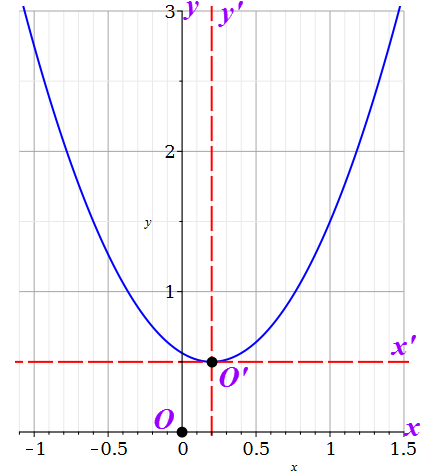  Решение Выполним построение в полярных координатах. Заполним таблицу
Построим график 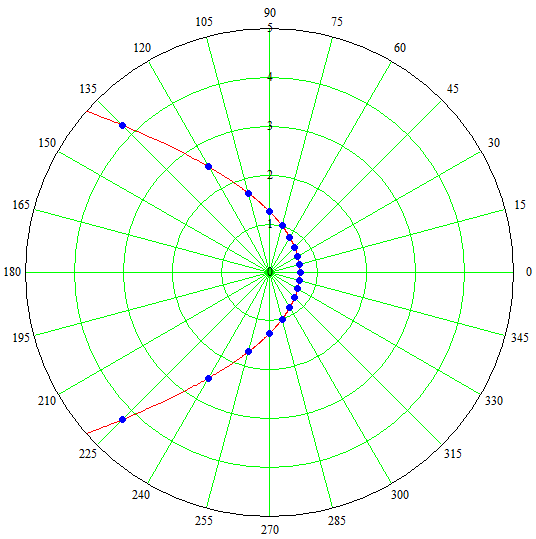 Преобразуем кривую 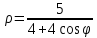 с помощью формул 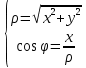 имеем 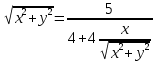 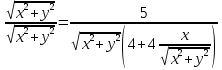 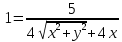 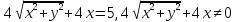 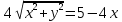 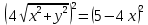 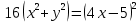 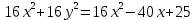 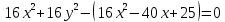 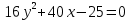 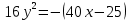 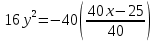 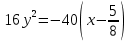 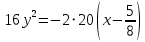 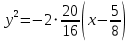 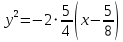 При параллельном переносе координат 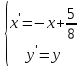 в новой системе координат кривая примет вид 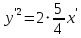 Это каноническое уравнение параболы с осью симметрии осью 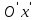 . Вершина параболы, совпадающая с началом новой (канонической) системы координат, в исходной системе имеет координаты . Вершина параболы, совпадающая с началом новой (канонической) системы координат, в исходной системе имеет координаты 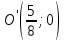 Ось 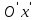 канонической системы координат противоположна оси канонической системы координат противоположна оси 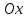 исходной системы координат, а оси ординат сонаправлены. исходной системы координат, а оси ординат сонаправлены.Заметим, что условие 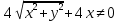 дает 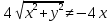 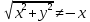 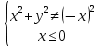 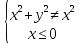 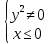 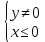 Это условие соответствует тому факту, что при 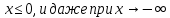 парабола никогда не пересечет ось 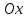 . . |