Равновесие частиц потоков жидкости, газа и газожидкостных смесей. Равновесие частиц потоков жидкости, газа и газожидкостных смесей. Скорость витания. Формула Риттингера
 Скачать 82.14 Kb. Скачать 82.14 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ НЕФТИ И ГАЗА (НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ) ИМЕНИ И.М. ГУБКИНА Кафедра «Бурение нефтяных и газовых скважин» РЕФЕРАТ по дисциплине «Гидроаэромеханика в бурении» на тему: «Равновесие частиц потоков жидкости, газа и газожидкостных смесей. Скорость витания. Формула Риттингера» Выполнил: студент группы РНМ-21-02 Карпович А.В. Проверил: профессор, д.т.н. Хавкин А.Я. Москва, 2021 ОглавлениеВведение 3 1. Вязкая жидкость 4 2. Вязкопластическая жидкость 8 3. Степенная жидкость 10 Заключение 11 Список литературы 12 3. https://www.ngpedia.ru/id567628p1.html (дата обращения 20.11.2021) 12 ВведениеПри бурении в скважине постоянно циркулирует поток жидкости (буровой раствор), которая нужна не только для удаления продуктов разрушения горной породы (шлама), но и для выполнения других, в равной степени важных функций, направленных на эффективное, экономичное и безопасное выполнение и завершение процесса бурения. Правильно подобранные параметры бурового раствора воспринимаются, как один из главных факторов, обеспечивающих эффективность всего процесса бурения. Твердые частицы горных пород, поступающие с забоя и стенок скважины, уносятся потоком промывочной жидкости, газа или газожидкостной смеси. В данной работе рассмотрены закономерности равновесия потоков вязкой, вязкопластической и степенной жидкостей с частицами породы на забое и в заколонном пространстве скважины. 1. Вязкая жидкость Рассмотрим движение твердой частицы со средней скоростью vч в восходящем вертикальном потоке жидкости, текущей со скоростью vп. В общем случае скорости потока и частицы относительно неподвижных стенок скважины разные, т. е.  ≠ ≠ 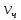 . .Обычно плотность частиц горных пород больше плотности жидкости, поэтому относительная скорость: 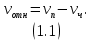 Принято, что частица, витая в потоке, имеет скорость vч = 0. Тогда скорость потока в (1) при vч =0 называется скоростью витания: 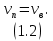 Таким образом, чтобы выбрать среднюю скорость потока, обеспечивающую транспорт частиц в кольцевом канале, нужно уметь определять скорости  и и 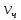 (рис 1, а). (рис 1, а).Равновесие частички в восходящем потоке обеспечивается равенством действующих на нее сил, схематично показанных на рис. 1, б. 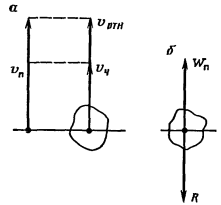 Рисунок 1 – Определение скорости витания частицы в жидкости (а) и действующих на нее сил (б) На частичку действует равнодействующая выталкивающей силы и силы тяжести 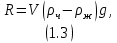 где 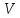 – объем частицы; – объем частицы;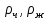 – плотности частицы и жидкости; – плотности частицы и жидкости; – ускорение свободного падения. – ускорение свободного падения.Сила R уравновешивается силой сопротивления Wп, которая зависит от реологических свойств жидкости, режима обтекания, концентрации и формы частиц. В дальнейшем будем рассматривать единичную сферическую частицу с эквивалентным диаметром  в неограниченной среде. Экспериментально установлено, что в этом случае частица при обтекании имеет наименьшее сопротивление. Скорость витания и расход, найденный с ее помощью, будут получены в виде оценок сверху. Формула для определения силы сопротивления частицы при обтекании ее вязкой жидкостью, согласно формуле Стокса, имеет вид в неограниченной среде. Экспериментально установлено, что в этом случае частица при обтекании имеет наименьшее сопротивление. Скорость витания и расход, найденный с ее помощью, будут получены в виде оценок сверху. Формула для определения силы сопротивления частицы при обтекании ее вязкой жидкостью, согласно формуле Стокса, имеет вид Эта формула справедлива для чисел   Рисунок 2 – Зависимость коэффициента сопротивления при обтекании частицы вязкой и вязкопластической жидкостью (переходные процессы не учтены) от чисел Хендстрема и Рейнольдса: 1 – кривая сопротивления Релея; 2 – для вязкой жидкости; 3 – нижний предел переходного режима (аппроксимация); 4-8 – для вязкопластической жидкости При любых значениях Re силу сопротивления можно выразить в общей форме: 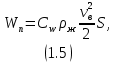 где 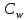 – коэффициент сопротивления, который можно определять по графику (рис. 2); – коэффициент сопротивления, который можно определять по графику (рис. 2);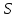 – площадь наибольшего сечения частицы, перпендикулярного к потоку. – площадь наибольшего сечения частицы, перпендикулярного к потоку.Формула (1.5) переходит в (1.4) при 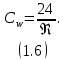 Приравнивая (1.3) и (1.5) и подставляя 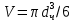 и и 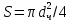 , получим скорость витания сферы , получим скорость витания сферы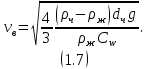 При (1.6) выражение (1.7) переходит в формулу 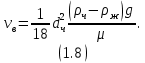 Формула (1.8) справедлива при Re<1. В области 1 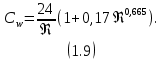 Для области 103≤Re<2·105 Ньютон принимал коэффициент 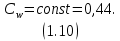 Для расчетов выноса шлама формулу (1.8) используют вплоть до числа Re = 60, т.к. она дает при этом несколько завышенные значения скорости  . Формулу (1.7) можно записать в виде . Формулу (1.7) можно записать в виде 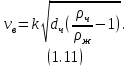 где 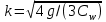 – постоянная Риттингера. – постоянная Риттингера.Согласно многочисленным данным, при обтекании сферы потоком с числом Re>60 примем 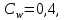 тогда тогда  Чтобы выбрать для расчета скорости витания соответствующую формулу, необходимо знать число Re, в которое также входит скорость  . Поэтому формулы (1.9), (1.8) и (1.11) применимы для вычисления . Поэтому формулы (1.9), (1.8) и (1.11) применимы для вычисления  методом последовательных приближений. Расчеты производятся следующим образом. Найдя по одной из формул скорость методом последовательных приближений. Расчеты производятся следующим образом. Найдя по одной из формул скорость  и затем число Re, следует проверить, лежит ли число Re в области применения этой формулы. При несовпадении результата необходимо использовать другую формулу. и затем число Re, следует проверить, лежит ли число Re в области применения этой формулы. При несовпадении результата необходимо использовать другую формулу.2. Вязкопластическая жидкость В отличие вязкой в вязкопластической жидкости различные сферы могут находиться в равновесии и при скорости 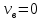 . Состояние шара, предшествующее движению, характеризуется предельным равновесием. В этом случае сила тяжести уравновешивается силой . Состояние шара, предшествующее движению, характеризуется предельным равновесием. В этом случае сила тяжести уравновешивается силой 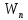 . Зависимость для . Зависимость для 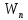 имеет вид имеет вид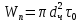 Приравнивая 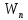 и R, определим максимальный диаметр частицы в ВПЖ: и R, определим максимальный диаметр частицы в ВПЖ: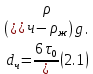 При движении шара в ВПЖ предположим, что суммируются сопротивления, обусловленные вязкостными и пластическими свойствами. 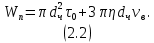 Следовательно, скорость витания частицы 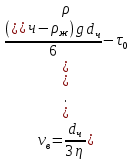 При 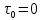 формула справедлива для вязкой жидкости и имеет вид (1.8). формула справедлива для вязкой жидкости и имеет вид (1.8).Значение коэффициента сопротивления 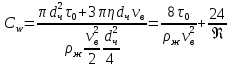 или 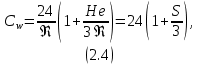 где 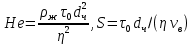 На рисунке 2 сплошной линией 1 представлена зависимость коэффициента сопротивления Сw от числа Re при He=0, построенная по многочисленным экспериментальным данным; линия 2 вместе с пунктирным ее продолжением описывается формулой Стокса; пунктирная линия 3 построена при Cw =0,4. Закон Стокса справедлив для Re<1, при 1 3. Степенная жидкость Для степенной жидкости можно принять, что сила сопротивления подчиняется также закону Стокса с поправкой, учитываемой показателем степени и подлежащей экспериментальному подтверждению: 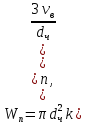 Где k, n – показатели консистенции. Приравнивая (3.1) и (1.3) для сферической частицы, получаем скорость витания 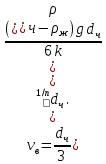 Находим выражение для коэффициента сопротивления степенной жидкости 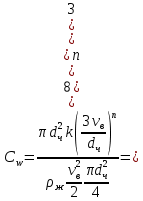 где 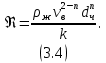 Заключение Следует отметить, что формулы (1.8), (1.11), (2.3) и (3.2) применимы для определения скорости всплытия пузырька газа в жидкости при значении разности плотностей, взятой по абсолютной величине. Они также могут быть полезны для оценки оседания частиц утяжелителя. Приведенные выше формулы справедливы для тех сред, которые соответствуют моделям вязкой, вязкопластической и степенной жидкостей. Для тиксотропных растворов применение этих формул возможно с помощью поправочного коэффициента k’, который можно найти в литературе. Данный коэффициент можно ввести в формулы, если заменить 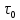 величиной величиной 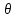 . .Список литературы Леонов Е.Г., Исаев В.И. Гидроаэромеханика в бурении: Учебник для вузов. — М.: Недра,1987. —304 с. Леонов Е.Г, Исаев В.И. Осложнения и аварии при бурении нефтяных и газовых скважин: учебник для вузов В 2 ч. Ч.1 Гидроаэромеханика в бурении [Текст], 2-е изд., испр. и доп. М.: Недра, 2006. – 413 с. 3. https://www.ngpedia.ru/id567628p1.html (дата обращения 20.11.2021) |
