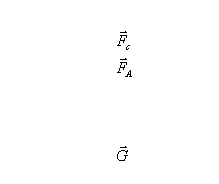Лабораторная работа № 2.1
ОПРЕДЕЛЕНИЕ ВЯЗКОСТИ ЖИДКОСТИ МЕТОДОМ СТОКСА
Цель работы: изучить метод Стокса, определить коэффициент динамической вязкости глицерина.
Приборы и принадлежности: виртуальная установка
1. ВЯЗКОСТЬ ЖИДКОСТИ. ЗАКОН СТОКСА
В жидкостях и газах при перемещении одних слоев относительно других возникают силы внутреннего трения, или вязкости, которые определяются законом Ньютона:
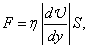 (1) (1)
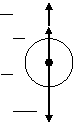
где коэффициент внутреннего трения, или коэффициент динамической вязкости, или просто вязкость; 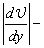 модуль градиента скорости, равный изменению скорости слоев жидкости на единицу длины в направлении нормали (в нашем случае вдоль оси y) к поверхности S соприкасающихся слоев (рис. 1). модуль градиента скорости, равный изменению скорости слоев жидкости на единицу длины в направлении нормали (в нашем случае вдоль оси y) к поверхности S соприкасающихся слоев (рис. 1).
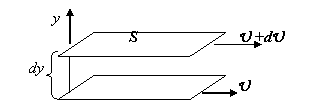
Рис. 1.
Согласно уравнению (1) коэффициент вязкости в СИ измеряется в Пас или в кг/(мс).
Механизм внутреннего трения в жидкостях и газах неодинаков, т.к. в них различен характер теплового движения молекул.
Вязкость жидкости обусловлена молекулярным взаимодействием, ограничивающим движение молекул. Каждая молекула жидкости находится в потенциальной яме, создаваемой соседними молекулами. Поэтому молекулы жидкости совершают колебательные движения около положения равновесия, то есть внутри потенциальной ямы. Глубина потенциальной ямы незначительно превышает среднюю кинетическую энергию, поэтому, получив дополнительную энергию при столкновении с другими молекулами, она может перескочить в новое положение равновесия.
Энергия, которую должна получить молекула, чтобы из одного положения перейти в другое, называется энергией активации W, а время нахождения молекулы в положении равновесия – временем «оседлой жизни» .
Перескок молекул между соседними положениями равновесия является случайным процессом. Вероятность того, что такой перескок произойдет за время одного периода 0, в соответствии с законом Больцмана, составляет
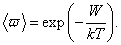 (2) (2)
Величина, обратная вероятности перехода молекулы 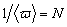 определяет среднее число колебаний, которое должна совершить молекула, чтобы покинуть положение равновесия. Среднее время «оседлой жизни» молекулы определяет среднее число колебаний, которое должна совершить молекула, чтобы покинуть положение равновесия. Среднее время «оседлой жизни» молекулы 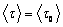 . .
Тогда
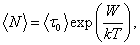 (3) (3)
где k – постоянная Больцмана; 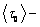 средний период колебаний молекулы около положения равновесия. средний период колебаний молекулы около положения равновесия.
Коэффициент динамической вязкости зависит от 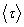 : чем реже молекулы меняют положение равновесия, тем больше вязкость. Используя модель скачков молекул, советский физик Я.И.Френкель показал, что вязкость изменяется по экспоненциальному закону: : чем реже молекулы меняют положение равновесия, тем больше вязкость. Используя модель скачков молекул, советский физик Я.И.Френкель показал, что вязкость изменяется по экспоненциальному закону:
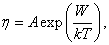 (4) (4)
где А – константа, определяемая свойствами жидкости.
Формула (4) является приближенной, но она достаточно хорошо описывает вязкость жидкости, например, воды в интервале температур от 5 до 100 С, глицерина – от 0 до 200 С.
Из формулы (4) видно, что с уменьшением температуры вязкость жидкости возрастает. В ряде случаев она становится настолько большой, что жидкость затвердевает без образования кристаллической решетки. В этом заключается механизм образования аморфных тел.
При малых скоростях движения тела в жидкости слой жидкости, непосредственно прилегающий к телу, прилипает к нему и движется со скоростью тела. По мере удаления от поверхности тела скорость слоев жидкости будет уменьшаться, но они будут двигаться параллельно. Такое слоистое движение жидкости называется ламинарным. При больших скоростях движения жидкости ламинарное движение жидкости становится неустойчивым и сменяется турбулентным, при котором частицы жидкости движутся по сложным траекториям со скоростями, изменяющимися беспорядочным образом. В результате происходит перемешивание жидкости и образуются вихри.
Характер движения жидкости определяется безразмерной величиной Re, называемой числом Рейнольдса. Это число зависит от формы тела и свойств жидкости. При движении шарика радиусом R со скоростью Uв жидкости плотностью ж
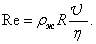 (5) (5)
При малых Re (<10), когда шарик радиусом 12 мм движется со скоростью 510 см/c в вязкой жидкости, например в глицерине, движение жидкости будет ламинарным. В этом случае на тело будет действовать сила сопротивления, пропорциональная скорости
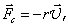 (6) (6)
где r – коэффициент сопротивления. Для тела сферической формы
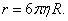
Сила сопротивления шарика радиусом R примет вид:
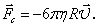 (7) (7)
Формула (7) называется законом Стокса.
2. ОПИСАНИЕ РАБОЧЕЙ УСТАНОВКИ И МЕТОДА
ИЗМЕРЕНИЙ
Одним из существующих методов определения коэффициента динамической вязкости является метод Стокса. Суть метода заключается в следующем. Если в сосуд с жидкостью бросить шарик плотностью большей, чем плотность жидкости (>ж), то он будет падать (рис. 2). На движущийся в жидкости шарик действует сила внутреннего трения (сила сопротивления) 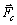 , тормозящая его движение и направленная вверх. Если считать, что стенки сосуда находятся на значительном расстоянии от движущегося шарика, то величину силы внутреннего трения можно определить по закону Стокса (6). , тормозящая его движение и направленная вверх. Если считать, что стенки сосуда находятся на значительном расстоянии от движущегося шарика, то величину силы внутреннего трения можно определить по закону Стокса (6).
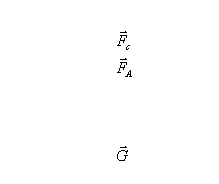
Рис. 2.
Кроме того, на падающий шарик действует сила тяжести, направленная вниз 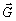 и выталкивающая сила и выталкивающая сила 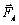 , направленная вверх. Запишем уравнение движения шарика в проекциях на направление движения: , направленная вверх. Запишем уравнение движения шарика в проекциях на направление движения:
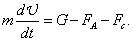 (8) (8)
Решение уравнения (8) описывает характер движения шарика на всех участках падения. В начале движения скорость шарика Uмала и силой Fc можно пренебречь, т.е. на начальном этапе шарик движется с ускорением
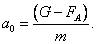
По мере увеличения скорости возрастает сила сопротивления и ускорение уменьшается. При большом времени движения сила сопротивления уравновешивается равнодействующей сил 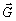 и и 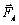 , и шарик будет двигаться равномерно с установившейся скоростью. Уравнение движения (8) в этом случае примет вид , и шарик будет двигаться равномерно с установившейся скоростью. Уравнение движения (8) в этом случае примет вид
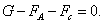 (9) (9)
Сила тяжести равна
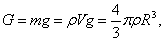 (10) (10)
где плотность вещества шарика.
Выталкивающая сила определяется по закону Архимеда:
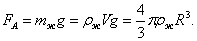 (11) (11)
Подставив (10), (11) и (7) в уравнение (9), получим
 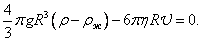
Отсюда находим
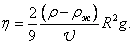 (12) (12)
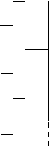
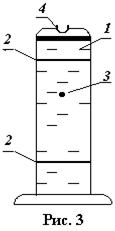
Установка представляет собой широкий стеклянный цилиндрический сосуд 1, наполненный исследуемой жидкостью (рис. 3). На сосуд надеты два резиновых кольца 2, расположенных друг от друга на расстоянии l. Если время движения шарика 3 между кольцами t, то скорость шарика при равномерном движении
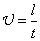
и формула (12) для определения коэффициента динамической вязкости запишется:
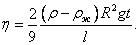 (13) (13)
При этом верхнее кольцо должно располагаться ниже уровня жидкости в сосуде, т.к. только на некоторой глубине силы, действующие на шарик, уравновешивают друг друга, шарик движется равномерно и формула (13) становится справедливой.
В сосуд через отверстие 4 опускают поочередно пять небольших шариков 3, плотность которых больше плотности исследуемой жидкости ж.
В опыте измеряют диаметры шариков, расстояние между кольцами и время движения каждого шарика на этом участке.
3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ОБРАБОТКА
РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
1. Познакомился с работой виртуальной лабораторной установки.
2. Провел пробные измерения для различных значений диаметра шарика d и расстояния между метками L, определяя время прохождения между метками при помощи секундомера.
3. Занес в таблицу заданные в варианте значения: расстояние Li между метками (верхней и нижней), диаметр шарика di и его плотность ш, а также плотность исследуемой жидкости ж.
4. Сбросил шарик в сосуд с жидкостью. В момент касания шариком верхней метки запустил секундомер, а в момент касания шариком нижней метки остановил его. Записал в таблицу показание секундомера ti.
5. Кнопкой “СБРОС” установил нуль на табло секундомера.
6. Повторил измерения пять раз, задавая различные значения диаметра шариков di и расстояние Li между метками.
7. Результаты опытов занес в таблицу измерений.
8. Вычислил коэффициент вязкости для каждого из пяти опытов по рабочей формуле (13).
9. Нашёл среднее значение коэффициента вязкости
10.Определил абсолютные приборные погрешности прямых измерений (расстояния между метками L, диаметра шарика d, времени его падения t, плотности шарика ш и жидкости ж), а также их относительные ошибки εL , εd , и εt .
11.Оценил полную абсолютную и относительную ε погрешности.
12. Записал конечный результат в виде .
13. Сравнил полученное значение со справочными данными.
14. По результатам эксперимента сделал выводы.
Таблица измерений
№
п/п
|
L, м
|
L, м
|
d, м
|
d, м
|
t, c
|
V, м/с
|
Re
|
, Пас
|
, Пас
|
(i)2 , (Пас)2
|
1
|
0, 4092
|
0,005
|
0,0031
|
0,000005
|
17,3
|
0,024
|
0,0064
|
1,465
|
0,0308
|
0,0009
|
2
|
0,4092
|
0,005
|
0,0036
|
0,000005
|
13,6
|
0,030
|
0,0088
|
1,542
|
0,0462
|
0,0021
|
3
|
0, 4612
|
0,005
|
0,0031
|
0,000005
|
14,6
|
0,032
|
0,0083
|
1,489
|
0,0068
|
0,00002
|
4
|
0,4612
|
0,005
|
0,0036
|
0,000005
|
20,4
|
0,023
|
0,0068
|
1,533
|
0,0372
|
0,0014
|
5
|
0,4360
|
0,005
|
0,0033
|
0,000005
|
16,4
|
0,027
|
0,0077
|
1,450
|
0,0458
|
0,0021
|
|
|
|
|
|
|
|
|
ср= 1,4958
|
ср= 0,0334
|
|
Расчёт погрешности коэффициента динамической вязкости по Стьюденту.
Отклонения от среднего: i =|ср – i |
1 =|ср –1 |=|1,4958–1.465|=0,0308 Па×с
Σ(i)2=0,00425
=0,95* (0,00425: (5*(5-1))=0,95*(0,00425: 20)=0,95*0,00021=0,0001
Относительная погрешность: ɛ = 0,0001/1,4958= 0,0007≈0,07%
Вывод: = (1,4958±0,0007) Пас
ɛ=0,07%
Сравнил полученный результат с табличным значением коэффициента динамической вязкости глицерина при соответствующей температуре. Температуру воздуха (а соответственно и глицерина) считать 20 градусов. И, полученный с помощью эксперимента результат, близок к табличному.
Коэффициенты динамической вязкости глицерина
при различных температурах
t, C
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
26
|
27
|
,Пас
|
1,74
|
1,62
|
1,48
|
1,35
|
1,23
|
1,124
|
1,024
|
0,934
|
0,85
|
0,78
|
|
Ответы на контрольные вопросы
Различают два типа течения вязкой жидкости – ламинарное и турбулентное. Турбулентным называется такое течение жидкости, при котором её частицы совершают неустановившееся и неупорядоченные движения по сложным траекториям, приводящим к перемешиванию слоёв. Ламинарное – это упорядоченное течение жидкости, при котором траектории движения соседних частиц мало отличаются друг от друга. При ламинарном течении жидкость можно рассматривать как совокупность отдельных слоёв, движущихся с различными скоростями. Это обусловлено тем, что при движении слоев жидкости относительно друг друга с различными скоростями между ними возникает тормозящая сила, это сила внутреннего трения или сила вязкости.
Вязкость – это свойство жидкости оказывать противодействие перемещению её слоёв относительно друг друга.
– коэффициент динамической вязкости, равный силе внутреннего трения, возникающей на единице поверхности соприкосновения слоев, движущихся относительно друг друга с градиентом скорости, равным единице.
В системе СИ коэффициент динамической вязкости измеряется в паскаль-секундах.
паскаль секунда Па с Н с / м кг/м с
Характер движения шарика определяется тремя действующими на него силами: силой тяжести mg , выталкивающей силой Архимеда FA и силой вязкого трения FC .
Различают два типа течения вязкой жидкости – ламинарное и турбулентное. Турбулентным называется такое течение жидкости, при котором её частицы совершают неустановившееся и неупорядоченные движения по сложным траекториям, приводящим к перемешиванию слоёв. Ламинарное – это упорядоченное течение жидкости, при котором траектории движения соседних частиц мало отличаются друг от друга.
Условия ламинарности можно считать выполненными, если число Рейнольдса
Re < Reкр. Критическое значение числа Рейнольдса для шарика Reкр, движущегося в жидкости, можно принять равным единицы.
Формула Стокса 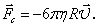 работает только при ламираном течении жидкости. работает только при ламираном течении жидкости.
Fтр=-6*3,14*1,5*1,5*10-3*0,75=-0,0078Н
Природа этих сил заключается в том, что слои жидкости, движущиеся с разными скоростями, обмениваются энергией: слои с молекулами, имеющими большую скорость, передают некоторое количество движения более медленным слоям, ускоряя их, но при этом сами подвергаются торможению. Ньютон показал, что сила внутреннего трения, действующая на средние слои, прямо пропорциональна градиенту скорости слоев в направлении, перпендикулярном течению.
Градиент скорости – это изменение скорости двух слоёв жидкости dV на расстоянии между слоями dX. Коэффициент динамической вязкости зависит от природы жидкости и уменьшается с повышением ее температуры.
Рабочая формула 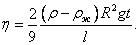 При этом верхнее кольцо должно располагаться ниже уровня жидкости в сосуде, т.к. только на некоторой глубине силы, действующие на шарик, уравновешивают друг друга, шарик движется равномерно и формула становится справедливой. При этом верхнее кольцо должно располагаться ниже уровня жидкости в сосуде, т.к. только на некоторой глубине силы, действующие на шарик, уравновешивают друг друга, шарик движется равномерно и формула становится справедливой.
Абсолютные приборные погрешности прямых измерений (расстояния между метками L, диаметра шарика d, времени его падения t, плотности шарика ш и жидкости ж), а также их относительные ошибки εL , εd , и εt .
|
 Скачать 57.61 Kb.
Скачать 57.61 Kb.