ЗАДАНИЯ тех.мех.. Разработал преподаватель Яковлева В. Д
 Скачать 203 Kb. Скачать 203 Kb.
|
|
ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ ПО «ТЕХНИЧЕСКОЙ МЕХАНИКЕ» И МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ЕЕ ВЫПОЛНЕНИЮ Разработал: преподаватель Яковлева В.Д. Контрольная работа составлена по многовариантной системе. В каждом варианте даны схемы и таблицы необходимых числовых данных. Вариант контрольной работы определяется по начальным буквам фамилии, полного имени и отчества. Все таб- лицы построены следующим образом : вертикальная левая крайняя графа содержит буквы алфавита, в вертикальной графе 1 указаны схемы к задаче, остальные вертикальные графы содержат числовые данные, необходимые для решения задачи. При выполнении контрольной работы необходимо соблюдать следующие требо- вания: - в контрольную работу следует записывать условие задач; - вычислениям должны предшествовать исходные формулы; - решение задач необходимо сопровождать пояснениями; задачи вначале решаются в общем виде, затем подставляются значения; - для всех исходных и вычисленных физических величин должна указываться раз- мерность; при этом следует иметь в виду, что числовые значения величин можно подстав- лять только в том случае, если их размерность совпадает. На обложке тетради указывается индекс учебной группы, фамилия, полное имя и отчество студента. Задания, выполненные не по своему варианту, не засчитываются и возвращают- ся студенту. ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ Задача 1. Определить аналитическим и графическим способами усилия в стержнях АВ и ВС заданной стержневой системы. Исходные данные для задачи своего варианта взять из таб- лицы. _____________________________________________________________________________ Алфавит | Ф | И | О | Ф | И | О Схема | F1, кН | F2, кН | α, град. | β, град. | γ, град. _____________________________________________________________________________ А, К, Ф 1 5 10 45 30 45 Б, Л, Х 2 6 12 30 90 60 В, М, Ц 3 7 14 90 60 45 Г, Н, Ч 4 8 16 60 30 60 Д, О, Ш 5 9 18 60 60 30 Е, П, Щ 1 10 20 30 30 60 Ё, Р, Ы 2 11 22 60 45 30 Ж, С, Э 3 12 24 60 60 30 З, Т, Ю 4 13 26 45 60 45 И, У, Я 5 14 28 30 45 60 _____________________________________________________________________________        A A A A A A        γ γ γ γ     B α F2 F1 B α F2 F1         γ β F1 α γ β F1 α    β C α β B β C α β B F   2 B C F2 C 2 B C F2 CF1 Схема 1 Схема 2 Схема 3  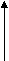 F1 F1    A A A A 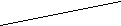     F2 B γ F2 B γ       β α β α  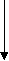    B α β B α β   γ F2 γ F2     F1 C C F1 C CСхема 4 Схема 5 Задача 2. Определить реакции опор балки, нагруженной, как показано на схеме. Исходные данные приведены в таблице. _____________________________________________________________________________ Алфавит | Ф | И | О | Ф | И | О | Ф | И | Схема | ℓ1, м | q, кН/ м | ℓ2, м | F, кН | α, град | М, кН∙м | ℓ3, м _____________________________________________________________________________ А, К, Ф 1 5,0 12 1,0 5,0 30 20 1,0 Б, Л, Х 2 4,0 10 2,0 10,0 60 18 2,0 В, М, Ц 3 3,0 8 3,0 15,0 45 16 3,0 Г, Н, Ч 4 2,0 6 4,0 20,0 90 14 4,0 Д, О, Ш 3 1,0 4 5,0 25,0 0 12 5,0 Е, П, Щ 1 2,0 12 5,0 5,0 30 10 1,0 Ё, Р, Ы 2 3,0 10 4,0 10,0 60 20 2,0 Ж, С, Э 3 4,0 8 3,0 15.0 45 18 3,0 З, Т, Ю 4 5,0 6 2,0 20,0 90 16 4,0 И, У, Я 2 1,0 4 1,0 25,0 0 14 5,0 _____________________________________________________________________________ Схема 1. Схема 3. 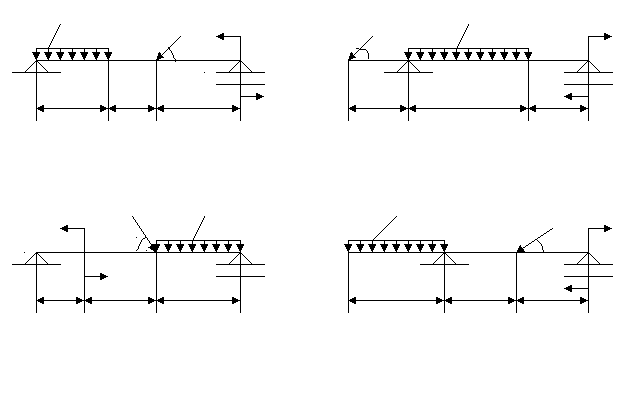 q F M F q M q F M F q Mα α ℓ1 ℓ2 ℓ3 ℓ1 ℓ2 ℓ3 Схема 2. Схема 4. М F q q F M α α ℓ1 ℓ2 ℓ3 ℓ1 ℓ2 ℓ3    Задача 3. Элемент металлической конструкции, несущий растягивающую нагрузку F, выполнен из двух полос сечением b × δ мм, соединенных семью заклепками d. Проверить прочность соединения, если полосы выполнены из Ст. 3, а заклепки – из Ст. 2; отверстия продавлены (срез заклепок, смятие полос и заклепок, растяжение нижней полосы в сече- ниях α × α и с × с); [τ cp.] = 100 MПа ; [σсм.] = 280 МПа ; [σ p] = 160 МПа. _____________________________________________________________________________ Алфавит |_____ Ф ______|_______ И ________|______ О ________|_______ Ф________ | F, кН | b, мм | δ, мм | d, мм _____________________________________________________________________________ А, К, Ф 100 90 5 10 Б, Л, Х 120 110 6 12 В, М, Ц 140 130 7 16 Г, Н, Ч 190 180 10 20 Д, О, Ш 160 150 8 18 Е, П, Щ 150 140 7 16 Ё, Р, Ы 110 100 5 10 Ж, С, Э 130 180 6 14 З, Т, Ю 170 160 8 18 И, У, Я 180 170 10 20 _____________________________________________________________________________ 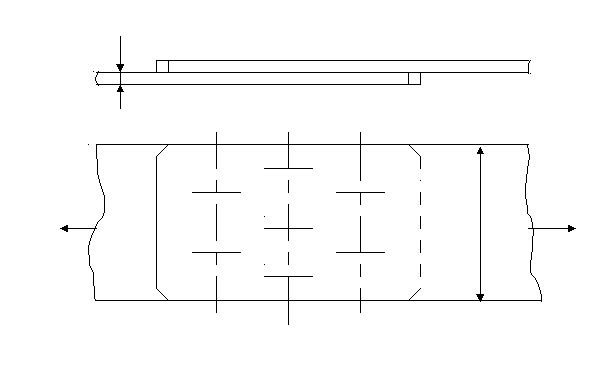 d о = d +1 мм δ α c F F b α c Задача 4. Для двух опорной балки построить эпюры изгибающих моментов и поперечных сил, подобрать сечение стального двутавра. Допускаемое напряжение [σ] = 160 МПа. _____________________________________________________________________________ Алфавит | Ф | И | О | Ф | И | О | Ф | Схема | F1, кН | F2, кН | М, кН∙м | α, м | b , м | c , м _____________________________________________________________________________ А, К, Ф 1 60 30 25 2,0 3,0 5,0 Б, Л, Х 2 50 40 30 5,0 3,0 2,0 В, М, Ц 3 40 50 40 4,0 4,0 2,0 Г, Н, Ч 4 30 40 20 2,0 6,0 2,0 Д, О, Ш 1 20 60 50 1,0 6,0 3,0 Е, П, Щ 2 40 30 15 2,0 5,0 4,0 Ё, Р, Ы 3 25 35 20 2,0 5,0 3,0 Ж, С, Э 4 35 40 45 1,0 4,0 5,0 З, Т, Ю 1 45 25 35 3,0 3,0 4,0 И, У, Я 2 15 35 20 4,0 3,0 3,0 _____________________________________________________________________________ Схема 1. Схема 3. F1 M F2 F1 M 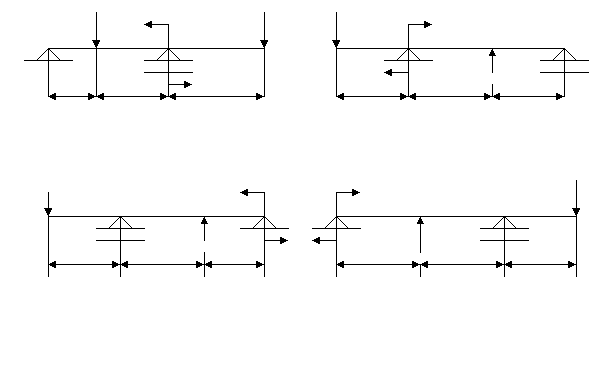 F2 α b c α b c Схема 2. Схема 4. F1 M M F2 F2 F1 α b c α b c ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ Пример 1. Определить аналитическим и графическим способами усилия в стерж- нях АВ и ВС заданной стержневой системы. Дано: F1 = 28 кН; F2 = 42 кН; α = 45°; β = 60°; γ = 30°. Определить реакции стержней RАВ и RВС. 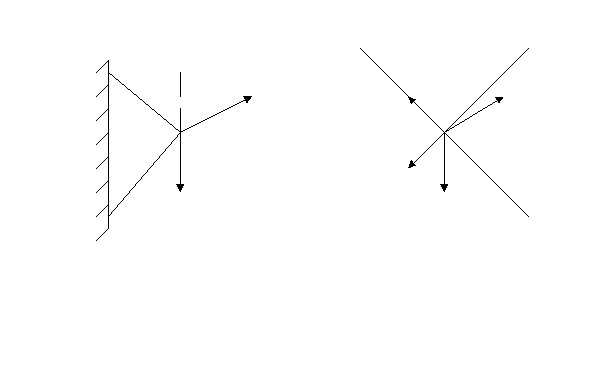 y А β F2 RAB F2 α B B 75° RBC 60° γ F1 F1 x C АНАЛИТИЧЕСКОЕ РЕШЕНИЕ:
отбросить связи АВ и ВС, заменив их реакциями RAB и RBC, направление реакций примем от узла В , считая стержни растянутыми;
ше отрицательных проекций; обозначим на схеме заданные углы и составим уравнения равновесия плоской системы сходящихся сил: Σ Fix = 0; F2 ∙ cos 75° + F1 ∙ cos 60° + RBC ∙ cos 90° - RAB ∙ cos 0° = 0; (1) Σ Fiy = 0; F2 ∙ cos 15° - F1 ∙ cos 30° - RBC ∙ cos 0° + RAB ∙ cos 90° = 0; (2) F2 ∙ cos 15° - F1 ∙ cos 30° Из уравнения (2) находим реакцию RBC = --------------------------------- . cos 0° 42 ∙ 0,966 – 28 ∙ 0,866 Подставляем числовые значения: RBC = -------------------------------- = 16,32 кН. 1 Найденное значение RBC подставляем в уравнение (1) и находим из него значение RAB: RAB = F2 ∙ cos 75° + F1 ∙ cos 60° + RBC ∙ cos 90°; RAB = 42 ∙ 0,259 + 28 ∙ 0,5 + 16,32 ∙ 0 = 24,88 кН. Ответ: RAB = 24,88 кН; RBC = 16,32 кН. Знаки указывают, что оба стержня растянуты. ГРАФИЧЕСКОЕ РЕШЕНИЕ: Выбрать масштаб сил m = 10 кН/см, тогда силы F1 и F2 ,будут откладываться отрезками: m F1 28 m F2 42 F1 = -- -- = ----- = 2,8 см ; F2 = ------ = ------ = 4,2 см. m 10 m 10 Из произвольно выбранной точки О отложить отрезок, соответствующий величине ( в масштабе) и направлению силы F1. Из конца этого отрезка отложить отрезок F2 (в масштабе). Так как условием равновесия плоской системы сходящихся сил является замкнутость силового многоугольника, то из начала отрезка F1 надо провести линию, па- раллельную вектору RBC, а из конца отрезка F2 провести линию, параллельную вектору RAB. Точка их пересечения является вершиной силового многоугольника. 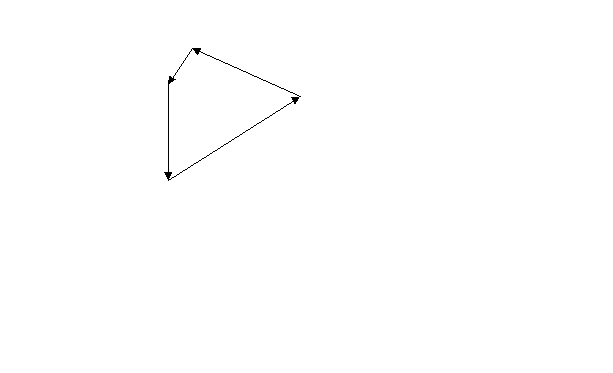 RBC RAB O (B) F1 F2 m m Измеряя отрезки RAB и RBC и умножая их на масштаб, найти значения RAB и RBC. m RAB = RAB ∙ m = 2,5 ∙ 10 = 25 кН; m RBC = RBC ∙ m = 1,62 ∙ 10 = 16,2 кН. Вычислить допущенную при графическом решении ошибку: 25 – 24,88 δAB = ------------- ∙ 100 % = 0,48 %; 24,88 16,32 – 16,2 δBC = ----------------- ∙ 100 % = 0,73 %. 16,32 Ошибка должна находиться в пределах 2 %. Ответ: а) аналитическое решение: RAB = 16,32 кН; RBC = 24,88 кН; б) графическое решение: RAB = 16,2 кН; RBC = 25 кН. Пример 2. Определить реакции опор балки, нагруженной, как показано на рисунке. Дано: F = 24кН; q = 6 кН/м; М = 12 кН∙м; ℓ1 = 1,8 м; ℓ2 = 5,2 м; ℓ3 = 3 м; α = 60°. Определить реакции опор RAx; RAy; RB. Решение: Обозначить опоры буквами А и В. Отбросить связи (опоры А и В), заменив их действие реакциями: неподвижная опора имеет реакции RAx (горизонтальная) и RAy(вертикальная) Подвижная опора – реакцию RB (вертикальная). Выбрать систему координат XУ с нача- лом в левой опоре. 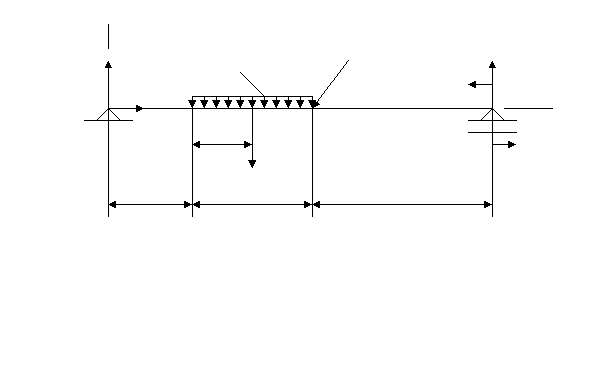 У УRB RAу q F RAx M A α B X 2,6 м q ∙ 5,2 1,8 м 5,2 м 3 м Для полученной произвольной плоской системы сил составить уравнения равно- весия: Σ Fix = 0; RAx – F ∙ cos 60° = 0; (1) Σ MA(Fi) = 0; q ∙ 5,2 ∙ ( 1,8 + 2,6 ) + F ∙ ( 1,8 + 5,2 ) ∙ sin 60° - M - RB ∙10 = 0; (2) Σ MB(Fi) = 0; RAу ∙ 10 – q ∙ 5,2 ∙ ( 2,6 + 3 ) - F ∙ 3 ∙ sin 60° - M = 0. (3) Из уравнения (1) находим: RAx = F ∙ cos 60° = 24 ∙ 0,5 = 12 кН. q ∙ 5,2 ∙ 4,4 + F ∙ 7 ∙ sin 60° - M Из уравнения (2) находим: RB = --------------------------------------; 10 6 ∙ 5,2 ∙ 4,4 + 24 ∙ 7 ∙ 0,866 - 12 RB = ------------------------------------- = 27,08 кН. 10 q ∙ 5,2 ∙ 5,6 + F ∙ 3 ∙ sin 60° + M Из уравнения (3) находим: RAу = --------------------------------------; 10 6 ∙ 5,2 ∙ 5,6 + 24 ∙ 3 ∙ 0,866 +12 RAу = -------------------------------------- = 24,9 кН. 10 Для проверки правильности решения составим сумму проекций всех сил на ось У: Σ Fiу = RAу - q ∙ 5,2 – F ∙ cos 30° + RB = 24,9 – 6 ∙ 5,2 – 24 ∙ 0,866 + 27,08 = = 51,98 – 51,984 = - 0,04 кН. Погрешность, полученная в результате вычислений, должна быть < 1 %. 0,04 δ = -------- ∙ 100 % = 0,077 % < 1 %. 51,984 Ответ: опорные реакции балки RAx = 12 кН; RAу = 24,9 кН; RB = 27,08 кН. Пример 3. Элемент металлической конструкции, несущий растягивающую нагрузку Q = 190 кН, выполнен из двух полос сечением b = 180 мм и δ = 10 мм, соеди- ненных семью заклепками диаметром d = 20 мм. Проверить прочность соединения, если [σ] p = 160 мПа; [τ] cp = 100 мПа; [ σ ] cм = 280 мПа. (рис.- см. задачу 3). Решение:
do = d + 1 мм = 20 + 1 = 21 мм. 2.Определяем рабочие (расчетные) напряжения и сравниваем их с допускаемыми: 4 ∙ Q 4 ∙ 190000 а) срез заклепок : τ ср = ------------- = ---------------------- = 78,4 мПа < [ τ ] ср i ∙ π ∙ do 2 7 ∙ 3,14∙ 212 б) смятие полос и заклепок: Q 190000 σ см = ---------------------- = ------------------------ = 129 мПа < [ σ ] cм i ∙ δ ∙ d o 7 ∙ 10 ∙ 21 в) растяжение нижней полосы: - в сечении α - α: Q 190000 σ р1 = ---------------------- = ------------------------ = 138 мПа < [ σ ] p (b – 2 d o) ∙ δ (180 – 2 ∙ 21) ∙ 10 - в сечении с – с: 5/7 ∙ Q 5/7 ∙ 190000 σ р2 = ---------------------- = ------------------------ = 116 мПа < [ σ ] p (b – 3 d o) ∙ δ (180 – 3 ∙ 21) ∙10 Вывод: Соединение недогружено. Соединение может выдержать нагрузку больше заданной. Пример 4. Для двух опорной балки построить эпюры поперечных сил Q и изгибающих моментов Ми. Подобрать сечение стального двутавра, если [σ] = 160 мПа. Дано: F1 = 24 кН; F2 = 36 кН; ℓ1 = 2,0 м; ℓ2 = 3,0 м; ℓ3 = 3,0 м; М1 = 18 кН∙м; М2 = 24 кН∙м. Z2 RA F2 RB  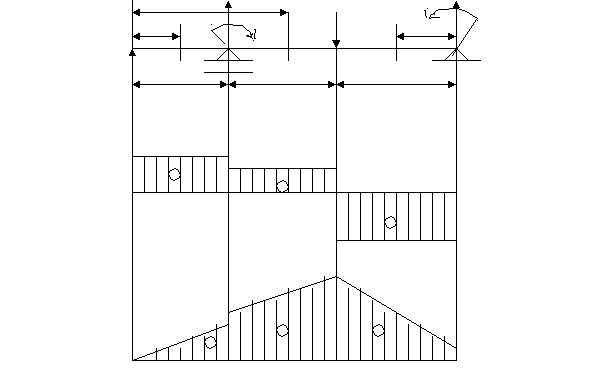 M2 M2Z1 M1 Z3 A B F1 2м 3м 3м Эпюра Q [кН] 24 11 0 - 25 Эпюра Ми [кНм] 99 66 48 24 0 Решение: Составляем уравнения равновесия, из которых определяем опорные реакции балки. ∑ МА(Fi) = 0; F1 ∙ 2 + M1 + F2 ∙ 3 – M2 – RB ∙ 6 = 0; (1) ∑ MB(Fi) = 0; F1 ∙ 8 + M1 + RA ∙ 6 – F2 ∙ 3 – M2 = 0. (2) Из уравнения (2) находим RA: - F1 ∙ 8 – M1 + F2 ∙ 3 + M2 - 24 ∙ 8 – 18 + 36 ∙ 3 + 24 RA = -------------------------------- = --------------------------------- = - 13 кН; 6 6 Из уравнения (1) находим RB: F1 ∙ 2 + M1 + F2 ∙ 3 – M2 24 ∙ 2 + 18 + 36 ∙ 3 – 24 RB = -------------------------------- = -------------------------------- = 25 кН.
Проверяем правильность определения опорных реакций, составляя сумму проекций всех сил на ось У: ∑ Fiy = 0; F1 + RA – F2 + RB = 24 + (- 13) - 36 + 25 = 0. Реакции определены верно. Делим балку на три участка. 1 участок. 0 ≤ Z1 ≤ 2 м Определяем поперечную силу на первом участке: Q1 = F1 = 24 кН – эпюра прямая, параллельная оси балки. Определяем изгибающий момент на первом участке: Ми1 = F1 ∙ Z1 - эпюра прямая, наклонная к оси балки, которую строим по двум точкам. 1 точка: Z1 = 0 → Mи1 = F1 ∙ 0 = 0; 2 точка: Z1 = 2 м → Ми1 = F1 ∙ 2 = 24 ∙ 2 = 48 кНм. 2 участок. 2 м ≤ Z2 ≤ 5 м Определяем поперечную силу на втором участке: Q2 = F1 + RA = 24 + (- 13) = 11 кН – эпюра прямая, параллельная оси балки. Определяем изгибающий момент на втором участке: Ми2 = F1 ∙ Z2 + RA ∙ (Z2 – 2) + M1 - эпюра прямая, наклонная к оси балки, которую строим по двум точкам. 1 точка: Z2 = 2 м → Ми2 = F1 ∙ 2 + RA ∙ (2 – 2) + M1 = 24 ∙ 2 + (- 13) ∙ 0 + 18 = 66 кНм; 2 точка: Z2 = 5 м → Ми2 = F1 ∙ 5 + RA ∙ (5 – 2) + M1 = 24 ∙ 5 + (- 13) ∙ 3 + 18 = 99 кНм. 3 участок. 0 ≤ Z3 ≤ 3 м Определяем поперечную силу на третьем участке: Q3 = - RB = - 25 кН – эпюра прямая, параллельная оси балки. Определяем изгибающий момент на третьем участке: Ми3 = RB ∙ Z3 + M2 - эпюра прямая, наклонная к оси балки, которую строим по двум точкам. 1 точка: Z3 = 0 → Ми3 = RВ ∙ 0 + M2 = 25 ∙ 0 + 24 = 24 кНм; 2 точка: Z3 = 3 м → Ми3 = RB ∙ 3 + M2 = 25 ∙ 3 + 24 = 99 кНм. По найденным значениям строим эпюры поперечных сил Q и изгибающих моментов Ми. По эпюре изгибающих моментов определяем положение опасного сечения балки (сечения, в котором изгибающий момент имеет наибольшее значение по абсолютной величине). Ми max = 99 кНм. | Mи max | Из условия прочности балки на изгиб σи = ------------ ≤ [σ] вычисляем необходимый Wx осевой момент сопротивления сечения: | Mи max | 99 ∙ 106 Н ∙ мм Wx ≥ ------------ ≥ --------------------- ≥ 0,619 ∙ 106 мм3 ≥ 619 см3 [σ] 160 Н/мм2 В соответствии с ГОСТ 8239 – 72 принимаем сечение из стального двутавра № 33 с Wx = 597 см3. | Mи max | 99 ∙ 106 Н ∙ мм Имеем напряжение: σи = ------------ = ---------------------- = 165,8 Н/мм2 Wx 597 ∙ 103 мм3 σи – [σ] 165,8 - 160 ∆ σ = ------------ = ----------------- ∙ 100% = 3,6% < 5%, что находится в [σ] 160 разрешенных пределах. Ответ: сечение балки – двутавр № 33. |
