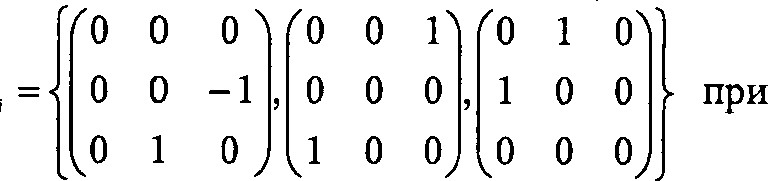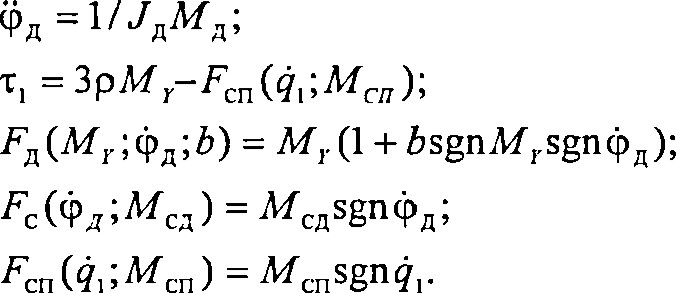Разработка и исследование системы автоматического управления технологическими операциями карьерного экскаваторамехлопаты

Название	Разработка и исследование системы автоматического управления технологическими операциями карьерного экскаваторамехлопаты
Дата	09.05.2022
Размер	2.14 Mb.
Формат файла
Имя файла	bobakob.docx
Тип	Исследование #518924

На правах рукописи

005053924

БАБАКОВ Сергей Евгеньевич

РАЗРАБОТКА И ИССЛЕДОВАНИЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО

УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМИ ОПЕРАЦИЯМИ КАРЬЕРНОГО

ЭКСКАВАТОРА-МЕХЛОПАТЫ

Специальность 05.13.06 — «Автоматизация и управление гехнологическими процессами и производствами» (промышленность)

автореферат

диссертации на соискание ученой степени кандидата технических наук

2 5 окт 2012

Москва 2012

Работа выполнена в ФГБОУ ВПО

«Московский государственный горный университет»

Научный руководитель доктор технических наук, профессор

ПЕВЗНЕР ЛЕОНИД ДАВИДОВИЧ

Официальные оппоненты доктор технических наук, профессор

СЛЕПЦОВ ВЛАДИМИР ВЛАДИМИРОВИЧ,

Московский государственный университет приборостроения и информатики

(МГУПИ), декан факультета приборостроения;

кандидат технических наук

ТРАВКИН ЕВГЕНИЙ КУЗЬМИЧ,

ЗАО «ПРОМТЕХ», главный инженер проекта

Ведущее предприятие

ФГУП «Национальный научный центр горного производства Институт горного дела имени А. А. Скочинского»

(Московская область, г. Люберцы).

Защита диссертации состоится ЗО октября 2012 г. в В час. на заседан диссертационного совета Д 212.128.07 при Московском государственном горн университете по адресу: 119991, г. Москва, Ленинский проспект, д. 6.

С диссертацией можно ознакомиться в библиотеке Московского государственного

горного университета

Автореферат разослан сентября 2012 г.

У

ченый секретарь диссертационного со доктор технических наук, профессор ЕНКО СМ.

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность работы. Проблема эффективного использования мощного карьерного экскаватора вызвана тем, что при ручном управлении сложной и высокопроизводительной машиной в специфических условиях горных работ невозможно достаточно длительно вести процесс экскавации на предельных скоростях и мощностях, что существенно уменьшает производительность машины. Выполнение операций экскаваторного цикла на высоких скоростях, особенно в сложных условиях и к КОШУ смены, ограничивается физическими возможностями человека, поэтому разница в производительности экскаватора, управляемого разными машинистами, может достигать порядка 4094. Длительность реального цикла экскавации часто значительно превышает паспортную в зависимости от квалификации машиниста, его психофизического состояния.

В современных условиях, когда предприятиям, эксплуатирующим карьерную технику, необходимо максимально эффективное её использование с целью повышения рентабельности, эта проблема становится особенно актуальной. Единственный путь решения проблемы — автоматизированное управление, помогающее машинисту или заменяющее его при выполнении операций технологического цикла экскаватора.

Проблема автоматизированного управления, известная еще с конца прошлого столетия, остается актуальной и сегодня. Причиной тому— слабая формализация выполняемых экскаватором операций, особенно операции черпания, и недостаточная развитость технических средств автоматизации и алгоритмического обеспечения систем управления экскаваторами.

Современный уровень развития техники с учетом успехов в смежных отраслях, такж как робототехника, позволяет дать новос решение проблемы автоматизированного управления.

Целью диссертационного исследования является разработка системы автоматического управления технологическими операциями черпания и транспортирования горной массы, позволяющей повысить эффективность использования карьерных экскаваторов-мехлопат.

Для достижения этой цели решаются следующие задачи:

разработка комплексной математической модели движения рабочего органа экскаватора-мехлопаты, учитывающей взаимовлияние поворотного, подъемного и напорного движений, взаимодействие ковша с забоем, для автоматического выполнения операций черпания и транспортирования горной массы;
разработка алгоритма управления транспортными движениями ковша экскаватора; разработка алгоритма управления сложной операцией черпания горной массы с применением методов искусственного интеллекта;
выполнение модельных исследований разработанных алгоритмов и оценка качества процессов управления.

Основная идея работы заключается в представлении модели карьерного экскаватора-мехлопаты как робота-манипулятора для решения задачи синтеза комбинационного алгоритма управления транспортными движениями ковша экскаватора и алгоритма управления операцией черпания горной массы. Защищаемые научные положения:

Метод построения математической модели движения рабочего органа экскаватора-мехлопаты, основанной на представлении расчетной схемы экскаватора в виде эквивалентного робота-манипулятора, отличающейся от известных большей вычислительной эффективностью.
Комплексная математическая модель движения рабочего органа и главных механизмов экскаватора-мехлопаты как объекта управления, в которой учитываются взаимовлияния главных механизмов, упругость подъемных и напорных канатов и которая позволяет непрерывно описывать движение ковша в операциях черпания и транспортирования.
Комбинационный алгоритм для системы автоматического управления транспортированием ковша экскаватора-мехлопаты, базирующийся на совместном использовании классических алгоритмов управления координатами состояния экскаватора с решением обратной задачи определения координат состояния экскаватора в зависимости от координат кромки ковша в базовой системе.
Алгоритм управления операцией черпания, основанный на методах нечеткой логики, позволяющий формировать текущее задание в виде рациональной толщины стружки и, не допуская перегрузки приводов, осуществлять автоматическое выполнение этого задания с требуемой точностью.

Научная новизна работы состоит в следующем:

предложенный метод модельного представления экскаватора-мехлопаты в виде эквивалентного робота-манипулятора отличается от известных методов значительной вычислительной эффективностью;
разработанная новая математическая модель движения ковша экскаватора позволяет учитывать взаимовлияние движений главных механизмов при выполнении операций экскаваторного цикла;

предложенный комбинированный алгоритм управления координатами ковша экскаватора в базовой системе координат, в отличие от известных, позволяет автоматической системе управления выполнять перенос ковша из одной точки в другую как с учетом, так и без учета формы траектории переноса;

разработанный алгоритм управления операцией черпания на основе методов нечеткой логики впервые позволяет в темпе реального времени определять рациональную текуи№о толщину стружки как задание системе управления и, не допуская перегрузки приводов, осуществлять автоматическое выполнение этого задания с требуемой точностью.

Обоснованность и достоверность полученных результатов подтверждается корректным прушенением известных методов описания динамики роботовманипуляторов. Достоверность моделирования процессов управления подтверждается допустимым уровнем соответствия с процессами в электромеханических системах главных механизмов реального экскаваторамехлопаты.

Практическое значение работы заключается в том, что:

методика построения математических моделей движения рабочего органа карьерных экскаваторов-мехлопат, включающая программы расчета коэффициентов модели и генерации их представления в среде «Sitnulinb> программы «МАТИВ», применима для описания отечественных и импортных экскаваторов; математическая модель позволяет синтезировать и настраивать параметры алгоритмов управления операциями экскаваторного цикла при построении систем автоматизации различных моделей карьерњж экскаваторов; разработанная структура системы автоматического управления технологическим процессом экскавации реализует с достаточным качеством полученные алгоритмы управления операциями полного экскаваторного цикла и применима в АСУТП мощных карьерных экскаваторов всех типов; предложенное аппаратное обеспечение системы управления на основе специализированного вычислителя отечественной разработки, удовлетворяющее горнотехнологическим условиям карьеров, позволяет реализовать не только разработанные алгоритмы управления операциями полного экскаваторного цикла, но и алгоритмы управления вспомогательными приводами и оборудованием экскаватора.

Реализация результатов работы. Модели и алгоритмы управления движениями ковша экскаватора при черпании и транспортировании горной породы запланированы к использованию ОАО «НИИВК им. М.А.Карцева» в опытноконструкторских работах. Предложенная структура системы управления и методика построения математических моделей карьерњж экскаваторов-мехлопат используются при чтении спецкурсов в процессе подготовки специалистов по направлению 220400 - «Автоматизация и управление».

Апробация работы. По материалам диссертации были сделаны доклады на научных семинарах кафедры «Автоматика и управление в технических системах», научных симпозиумах «Неделя горняка» в 2010, 2011, 2012 годах, на конференции молодых специалистов ОАО «НИИВК им. М.А. Карцева» в 2010 году, международном семинаре «Современные технологии в задачах управления, автоматики и обработки информации», г. Алушта, 2011 г.

Публикации. По теме диссертации опубликовано 7 научных работ, в том числе 4 статьи в изданиях по перечню ВАК Минобрнауки России.

Структура диссертации. Диссертация состоит из введения, 5 глав и заключения, содержит 76 рисунков, 5 таблиц, список литературы из 78 наименований и три приложения.

ОСНОВНОЕ СОДЕРЖАКШЕ РАБОТЫ

В первой главе ставится задача разработки и исследования системы автоматического управления технологическими операциями карьерного экскаватора. Приводится обзор современного состояния проблемы автоматизации карьерных экскаваторов, в том числе карьерных мехлопат.

В обзоре показано, что интерес к проблеме создания систем автоматического управления мощными карьерными экскаваторами проистекает из 60-х годов прошлого столетия. Значительный вклад в решение этой проблемы для экскаваторов-драглайнов внесли такие ученые, как О.А. Залесов, МС. Ломакин, Л.Д. Певзнер, Л.И.Толпежников, Г.Б. Петерс, А.Д. Яризов, А.Е. Троп, М.Б. Носырев, Ю.М. Иржак, А.Л. Карякин, В.М. Остриров, В.Я. Ткаченко.

Отдельные задачи автоматизации рабочего процесса карьерного экскаваторамехлопаты изучались в Киевском институте автоматики. Была предложена система автоматического управления циклом экскавации карьерного экскаватора ЭКГ-4,6. Решались задачи автоматического управления процессом копания, полуавтоматического управления поворотом платформы, стабилизации характеристик электроприводов.

В Московском горном институте значительный вклад в решение задач автоматизации транспортных операций карьерного экскаватора внесен В.А. Кравцовым. Им был пртаенен новый подход к математическому описаншо

движения ковша мехлопаты, а именно представление расчетной схемы экскаватора в виде эквивалентного манипуляционного робота и применения к нему методов описания манипуляторов, используемых в робототехнике.

На современном этапе можно выделить две группы исследовательских работ.

Первую группу составляют работы А.А. Годжиева, А.В. Кулыгина, И. Ю. Семыкиной и др. по автоматващш и совершенствованию электроприводов карьерных экскаваторов. Вторую - работы Л.Д. Певзнера, АЛ. Мейлахса, Т. Линна по интеллектуализации систем управления и мониторинга процесса экскавации.

А.А. Годжиев, исследовав подъемно-напорный механизм экскаватора ЭКГ8И, предложил инженерную методику синтеза системы автоматического управления двухмассовой электромеханической системой с гибкой отрицательной обратной связью по нагрузке в упругом звене.

Новое направление в автоматизации мощных экскаваторов — применение методов искусственного интеллекта для построения систем мониторинга и идентификации рабочего процесса экскаватора и управления отдельными операциями этого процесса.

В работе АЛ. Мейлахса рассматриваются алгоритмы управления драглайном, использующие опыт квалифицированных машинистов, которые обеспечивают почти оптимальные и безопасные движения ковша и позволяют снижать динамические воздействия от его раскачивания. Эти алгоритмы основаны на применении методов нечеткой логики и нейронных сетей интеллектуального управления.

Автором предложен метод геометрического синтеза кусочно-предельных траекторий плоского движения ковша, позволяощшй формировать программные как традиционные транспортные движения, так и дтгжения нового технологического типа. Этот метод базируется на представлении траектории движения ковша в виде частей различных предельных траекторий, отвечающих максимальным управляющим заданиям приводам тяги и подъема. Выполнен синтез предельных траекторий для транспортных движений на черпания и на разгрузку. Эти траектории были использованы им при разработке алгоритмов управления приводами в качестве эталонных, по которым в идеале должен двигаться ковш. Предложены варианты нечетких алгоритмов управления приводами подъема и тяги для реализации траекторного движения в рабочем пространстве.

В работе рассмотрен регулятор управления поворотным движением платформы со структурой нечеткой нейронной сети. Этот алгоритм обладает свойством адаптировать свои параметры, «доучиваться» в процессе реального управления, что позволяет обеспечить заданное качество позиционирования ковша, инвариантно по отношению к изменению параметров динамических процессов в электроприводах главных механизмов драглайна и внешней технологической обстановки в условиях существенной неопределенности.

Выполненный на основе обзора анализ позволил сформулировать задачи диссертационных исследований:

разработать комплексную матемашческуо модель экскаватора-мехлопаты как объекта управления, учитывающую взаимовлияние поворотного, подъемного и напорного движений, взаимодействие ковша с забоем.
разработать имитационную модель экскаватора-мехлопаты для операций черпания и транспортирования горной массы;
разработать алгоритм управления транспортными движениями ковша;
разработать алгоритм управления операцией черпания горной массы с применением элементов нечеткой логики;
выполнить модельные исследования разработанных алгоритмов, оценить качество процессов управления

Вторая глава посвящена вопросам разработки математической модели движения рабочего органа карьерного экскаватор-мехлопаты методом эквивалентного манипуляционного робота. Идея построения модели заключается в сведении расчетной схемы экскаватора к схеме эквивалентного манипулятора с последующим применением к ней процедуры описания динамики и кинематики, базирующейся на структурном подходе в варианте, разработанном в ИПМ кш. М.В.Келдыша.

Сведение расчетной схемы экскаватора к схеме эквивалентного манипулятора включает в себя выполнение трех операций:

устранение голономной связи через подъемный канат, с заменой ее действия силой, равной реакции этой связи;

представление кинематической пары в подъемно-напорном механизме в виде композиции вращательного и поступательного сочленений;

приведение движущих моментов механизмов к осям сочленений.

После выполнения этих преобразований расчетная схема механической системы карьерного экскаватора принимает вид, показанный на рис. В этой схеме кинематическая цепь экскаватора является разомкнутой и включает элементарные звенья:

подвижное основание — нижняя рама с ходовой тележкой; поворотную платформу с размещенным на ней оборудованием, соединенную с основанием через вращательное сочленение; стрелу, связанную с платформой шарнирным сочленением;
седловой подшипник, соединенный со стрелой через шарнирное сочленение; рукоять с ковшом, совершающую поступательное движение относительно седлового подшипника.

При этом стрела считается «фиктивным» звеном, которое введено только для упрощения формирования уравнений движения системы. Звенья соединены между

собой при помощи шарниров

Рис 1. Эквивалентная расчетная манипуляционная схема экскаватора-мехлопаты

Согласно процедуре метода ИТЛ им. М.В.Келдыша звено — рукоять с ковшом разбиваем на два отдельњж звена— рукоять и ковш и в месте перехода рукояти в ковш вводим дополнительный фиктивный вращательный шарнир 05 и дополнительный фиктивный угол О . Место крепления поворотной платформы на подвижную основу принято за основание манипулятора. При этом полагаем, что в ходе технологического цикла подвижное основание экскаватора не совершает движений, а при перемещении экскаватора положения всех звеньев фиксированы.

Введем неподвижную — базовую систему координат и несколько подвижных систем координат, связанных со звеньями эквивалентного манипулятора. В этих системах определены обобщенные координаты:

ql — угол поворота платформы вокруг свой оси;

— угол наклона стрелы экскаватора;

— угол наклона седлового подшипника; q4 — выдвижение рукояти; q5 — фиктивный угол поворота ковша экскаватора.

Далее, следуя процедуре описания кинематики манипулятора, найдем векторы переноса центров систем координат и матрицы поворотов систем координат вокруг соответствующих осей. Они принимают вид: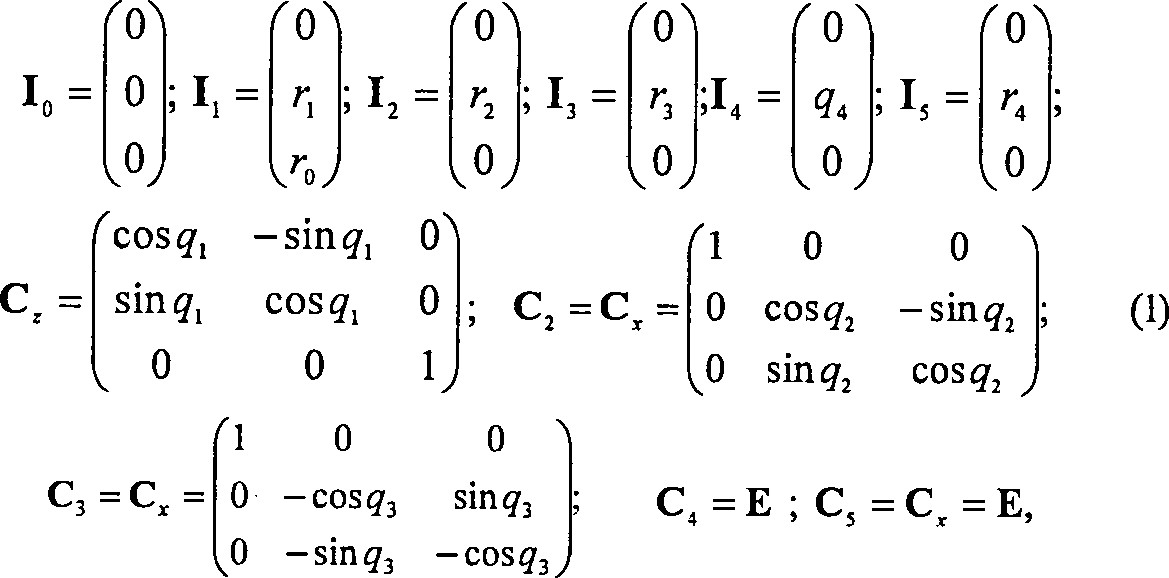

расстояние от центра поворотного редуктора до поворотной платформы;

— расстояние от оси вращения поворотной платформы до места крепления стрелы;

— длина секции стрелы от места крепления до оси седлового подшипника; — половина длины седлового подшипника;

— расстояние от центра фиктивного пятого шарнира до наружней кромки зубьев ковша экскаватора.

Находта аналитические зависимости координат зубьев ковша экскаватора как функции обобщенных координат, для чего используем соотношения для координат схвата эквивалентного манипулятора в неподвижной системе:

R о = Sq,I, = сд +qc,I, +ср,сзц +сяс,сзсд, +qqqc,csI,. (2)

Определены поверхности, описываемые кромкой ковша экскаватора в функции угла поворота платформы и угла наклона рукояти при различных выдвижениях рукояти.

Из геометрических соображений находим решение обратной задачи определения обобщенных координат экскаватора в зависимости от координат кромки зубьев ковша в базовой системе. Выражения координаты ф для физически существующих значений ттеют вид:

для случая, когда рукоять находится ниже своего горизонтального

положения,

— + arctg 4

(3)

для случая, когда рукоять находится выше своего горизонтального положения, т.е. z -+ r

(4)

Для обобщенных коодинат q4 и ф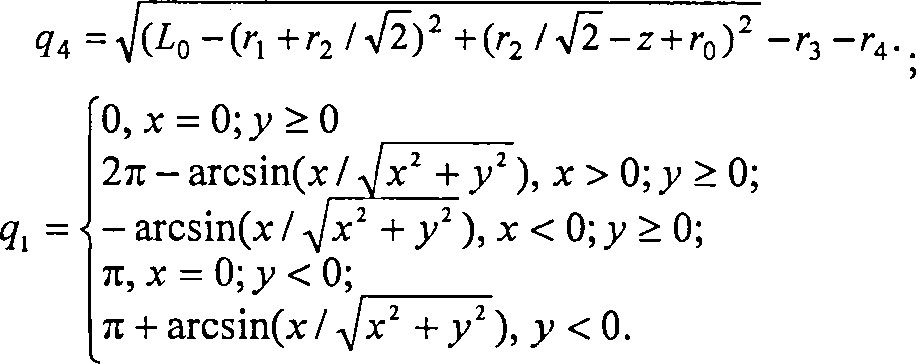

(

5)

(6)

Выполнено построение системы уравнений динамики экскаватора в виде системы уравнений Лагранжа П рода, загшсанной для эквивалентного манипулятора:

к = 1,5 (7)

и в матричной форме:

где D(q)— симметричная, положительно определенная матрица инерции манипулятора с элементами 4 ; h(q, 4) — вектор кориолисовых и центробежных сил 11 к = Ehk;tqsqr ;

р — вектор гравитационных сил с компонентами; т — вектор моментов обобщенных сил в шарнирах, обусловленный работой приводов и воздействием внешних нагрузок.

Выражения для вычисления коэффициентов уравнений Лагранжа:

(8)

РК =E -Ti

i=k р=к где т, — масса Ьтого звена; g — вектор ускорений свободного падения.

В этих уравнениях используются компоненты скоростей ковша экскаватора, вычисляемые при помощи соотношений:

(1 —indp)+Clpindp /qp s р vps ...cs_pscs

в которых 2 вспомогательные матрицы, используемые для вычисления

производных от матриц поворотов

соответственно.

Параметр inds характеризует тип шарнира: ind. для вращательного шарнира, inds=O для поступательного.

6qs rc. +1 indf ,p=i

где rc,I — вектор координат центра масс Ьтого звена в Ьтой системе координат,

Ј. = .Ј. — .r{., И— матрица инерции Ьтого звена манипулятора.

Матрица инерции звена манипулятора вычисляется через компоненты тензора инерции манипулятора. Для вычисления тензоров инерции звеньев эквивалентного манипулятора звенья представлялись телами правильной геометрической формы.

Найденные координаты центров масс звеньев позволили определить в символьном виде коэффициенты уравнений динамики модели экскаватора ЭКГ- 15: ^d114l +hllN143 + Дзмзш

4343 +4444 +h3114141 + + -4344344 +h3414441 +h3444444 + +4434443 + Рз = ^тз ;

d4343 +4444 +h4114141 + + р4 = т,.

Расчет производился с применением Symbolic Math ТооЉох программы МАТИВ.

Для получения выражений обобщенных моментов и сил, прикладываемых к звеньям, использовалась расчетная схема, представленная на рис. 2.

Механизм поворота

Рис. 2. К выводу уравнений обобщенных моментов и сил

Для получения момента, развиваемого механизмом поворота, были использованы соотношения, приведенные в работе А.Л. Мейлахса:

м = зм

Му =

где

д, • л — угол поворота вала двигателя и круговая частота его вращения; Мд — момент, развиваемый одним двигателем;

Мэ — электромагнитный момент двигателя привода;

Му — упругий момент валопровода, приведенный к валу двигателя; мсд, мсп — абсолютные значения моментов статического сопротивления движению двигателя и поворотной платформы;

Ед(... ) — динамический момент сил сопротивления движению; Ь — коэффициент, связанный с КПД механизма поворота; р, ос — передаточное число редуктора механизма поворота и приведенный к валу двигателя угол закручивания валопровода;

К, д — приведенные к валу двигателя жесткость валопровода и величина кинематического зазора;

.Јд — момент инерции двигателя.

Для вывода уравнений обобщенных моментов третьего и четвертого звеньев использовалась схема, представленная на рис. З, где видно, что на рукоять действует вращающей момент, создаваемый проекцией силы натяжения подъемного каната на ось, перпендикулярную рукояти:

СЗ = 22д ф4 + П

(13)

где —упругая сила в подъемном канате.

Выражение для упругой силы, возникающей в подъемном канате, имеет вид:

—)

под под м

(14)

под ред пол где Мупр.мех — упругий момент в механизме подъема, приведенный к вторичному валу редуктора;

— радиус подъемного барабана;

— передаточное отношение редуктора;

— передаточное отношение полиспаста; подлек — жесткость подъемного каната, приведенная к вторичному валу редуктора;

Уп — скорость движения подъемного каната, вычисляемая из соотношения

Lsin

полsincp=

в котором

—длина участка подъемного каната от головного блока стрелы до блока к рукояти в данный момент.

Выражение обобщенной силы, действующей на четвертое звено-рукоять, имеет вид

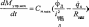
Т 4 = — cosp. (16) В этом выражении — усилие в напорном канате, — усилие в подъемном канате, которое определяется соотношением

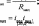упр. мех (17)

где Муир.мех — упругий момент, создаваемый механизмом напора, приведенный к вторичному валу редуктора;

— радиус напорного барабана;

— передаточное отношение редуктора;

— передаточное отношение полиспаста; снап.мех— жесткость напорного каната, приведенная к вторичному валу редуктора.

В третьей главе представлены динамические модели экскаватора- мехлопаты, выполняющего операции транспортирования и черпания горной массы. Для их построения к системе уравнений динамики (11) и выражениям для обобщенных моментов (12, 13, 16) были добавлены математические модели главных электроприводов экскаватора, выполненные на основе оптимальной структуры экскаваторного электропривода по системе ТП-Г-Д с двухконтурной системой управления током якорной цепи и ЭДС генератора.

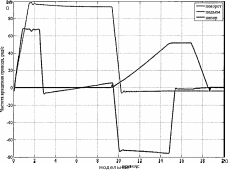
Настройка контуров системы регулирования выполнялась по критерию модульного оптимума. Кривые переходных процессов разгона и торможения механизмов поворота, напора и подъема достаточно близки, как видно из рис. 3, к реальным.

Модель экскаватора, выполняющего операции транспортирования, представленная на рис. 4, состоит из трех основных подмоделей: модель «Motors» представляет динамику электроприводов и канатной системы экскаватора, модель «Excavator» представляет динамику механической части экскаватора и

модель «kinem», где выполняются вычисления координат ковша в базовой системе. Команды машиниста имитируются блоком «Signal Buildem. Модель учитывает рост массы ковша в процессе черпания. Подсистема «Motors» состоит из трех блоков моделей приводов и блоков вычисления обобщенных моментов в канатной системе. Подсистема «Excavator» содержит три блока моделей уравнений динамики движения звеньев. Модель позволяет получать переходные процессы по скоростям, токам и ускорениям в приводах, скоростям и ускорения обобщенных координат, длине и скорости ее изменения для подъемного каната, обобщенным координатам, координатам ковша в базовой системе.

80

60

а.

-40

-60

Рис З . Скорости главных приводов экскаватора, полученные в процессе моделирования

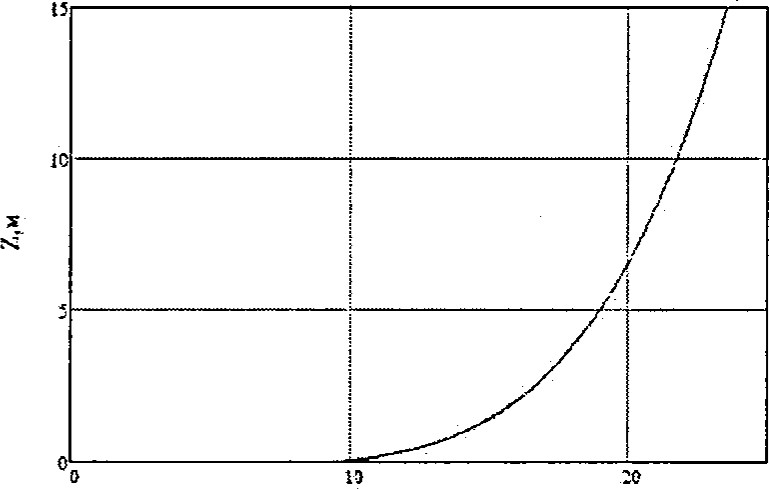
Динамическая модель экскаватора, выполняющего операцию черпания содержит модельное представление добычного забоя как кусочно-степенной функции, основным элементом которой является полином п-того порядка. При этом кривая забоя проходит через две характерные точки

tgu

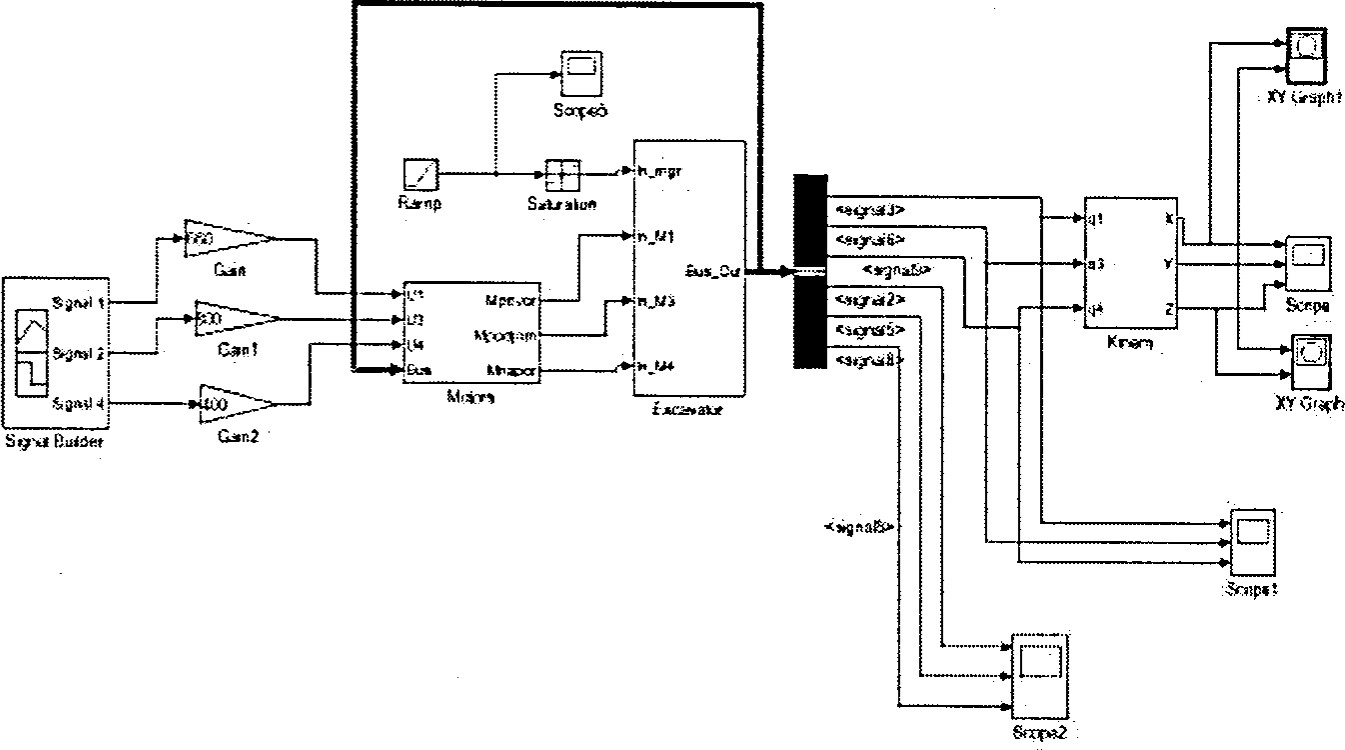
Рис 4. Динамическая модель экскаватора-мехлопаты для транспортных операций Уравнение кривой имеет вид:

h

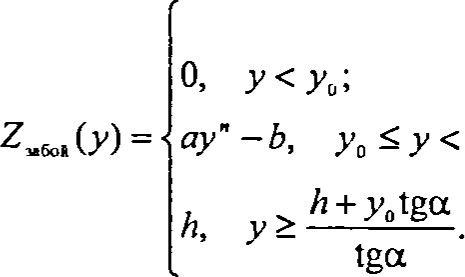+ уо tgu tga

где — высота забоя; а — угол естественного откоса; уо — координата точки излома.

К модели динамики добавлены выражения для моментов сил сопротивления породы копанию, имеющие вид:

+ Л + r4)ab;

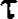= 0,1kNb,

где а — толщина снимаемой стружки; Ь — ширина ковша;

— обобщенный коэффициент сопротивления породы копанию.

В главе приводится выражение для толщины снимаемой стружки и оценка степени наполнения ковша. Также приводятся результаты моделирования процесса черпания экскаватора-мехлопаты.

В четвертой главе решаются задачи разработки алгоритмов управления операциями экскаваторного цикла. Рассматривается система автоматического управления обобщенными координатами экскаватора.

15

Система управления обобщенными координатами является системой подчиненного регулирования, в которой к каждому из главных приводов добавлен контур управления соответствующей координатой. Каждый КОНТУР содержит Прегулятор, настроенный при помощи программы «Simulink Response 0ptiTization». Критериями настройки являлось наличие апериодического переходного процесса при максимальном быстродействии.

Показано, что настроенная система управления обобщенными координатами совместно с решением обратной задачи определения обобщенных координат в зависимости от координат ковша экскаватора может быть использована для управления транспортными движениями ковша. Причем как без отслеживания траектории, так и с отработкой. Выделены следующие этапы управления транспортными движениями ковша по заданной траектории:

Расчет начальной и конечной точек траектории;
Определение промежуточных точек траектории, если этого требует текущая обстановка;

З. Пространственное представление траектории путем интерполяции выбранного множества точек сплайнами или кусками других кривых;

Пространственно-временное представление траектории, при котором для опорных точек добавляется четвертая координата время от момента начала отработки траектории, в которое ковш должен быть в данной точке;
Отработка пространственно-временной траектории при помощи решения обратной задачи определения обобщенных координат экскаватора и системы управления ими.

Уд а

16

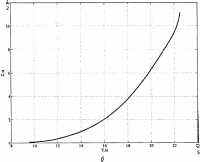
Рис. 5. Траектория задания а и отработанная системой траектория б

В главе приводится алгоритм управления операцией черпания с применением нечеткой логики. Идея алгоритма заключается в том, что первоначально выполняется проверка на возможность стопорения главњж приводов при выполнении задания на черпание. Если может 1шеть место ситуация стопорения, то управление приводами осуществляется по заранее заложенной программе, если нет, то управление осуществляется при помощи алгоритма, построенного на основе нечеткой логики.

Алгоритм управления черпанием на основе нечеткой логики состоит из трех алгоритмических блоков. Первый блок представляет собой алгоритм определения задания толщины стружки, которую должен снять ковш. Алгоритм использует три лингвистические переменные: «нагрузка привоДа поДъема», «заглубление зубьев ковша», «толщина стружки» и базу из 12-правил. Суть правил заключается в формировании задания максимально возможной толщины стружки при условии отсутствия перегрузки приводов.

Второй алгоритмический блок — алгоритм управления приводом напора, отрабатывающий заданную первым блоком или оператором толщину стружки. Алгоритм использует четыре лингвистические переменные: «ошибка отработки задания», «степень заглубления ковша», «высота зубьев ковша», «скорость привоДа напора» и базу из 14 правил. При этом под степенью заглубления ковша здесь понимается толщина снимаемой стружки, взятая со знаком «паюс», если ковш введен в забой, и «минус» - если ковш вне забоя, иначе говоря, «отрицательная» толщина модельной стружки характеризует степень отдаления ковша от забоя.

Перечень продукционных правил, на которых основывается данный алгоритм управления, приведен ниже.

П 1: Если «степень заглубления» ковша большая положительная и «высота зубьев ковша» ниже рабочей, то «скорость привоДа напора» должна быть большой отрицательной;

П2: Если «степень заглубления» маленькая положительная и «высота зубьев ковша» ниже рабочей, то «скорость привоДа напора» должна быть большой отрицательной;

ПЗ: Если «степень заглубления» маленькая отрицательная и «высота зубьев ковша» нтке рабочей, то «скорость привоДа напора» должна быть большой положительной;

Ш: Если «степень заглубления» большая отрицательная и «высота зубьев ковша» ниже рабочей, то «скорость привоДа напора» должна быть большой положительной;

П5: Если «ошибка отработки задания» большая отрицательная и «высота зубьев ковша» рабочая, то «скорость привоДа напора» должна быть большой отрицательной;

Пб: Если «ошибка отработки заДания» малая отрицательная и «высота зубьев ковша» рабочая, то «скорость привоДа напора» должна быть большой отрицательной;

П7: Если «ошибка отработки заДания» нулевая и «высота зубьев ковша» рабочая, то «скорость привоДа напора» — нуль;

П8: Если «ошибка отработки заДания» малая положительная и «высота зубьев ковша» рабочая, то «скорость привоДа напора» должна быть большой положительной;

П9: Если «ошибка отработки заДания» большая положительная и «высота зубьев ковша» рабочая, то «скорость привоДа напора» должна быть большой положительной;

ГН 0: Если «ошибка отработки задания» большая положительная и «высота зубьев ковша» выше рабочей, то «скорость привоДа напора» должна быть большой положительной;

ПИ: Если «ошибка отработки задания» маленькая положительная и «высота зубьев ковша» выше рабочей, то «скорость привоДа напора» должна быть большой положительной;

18

П 12: Если «ошибка отработки заДания» маленькая отрицательная и «высота зубьев ковша» выше рабочей, то «скорость призоДа напора» должна быть маленькой положительной;

П 13: Если «ошибка отработки заДания» нулевая и «высота зубьев ковша» выше рабочей, то «скорость призоДа напора» — нуль;

П 14: Если «ошибка отработки задания» большая отрицательная и «высота зубьев ковша» выше рабочей, то «скорость привоДа напора» должна быть маленькой отрицательной.

Алгоритм реализует три стратегии управления в зависимости от принадлежности значения текущего положения ковша относительно забоя трем промежуткам значений, названным: «рабочий интервал», «меньше рабочего», «больше рабочего». В «рабочем» интервале значений реализуется стратегия строгой отработки задания, являющаяся управлением по рассогласованию. В интервале шеньше рабочего» реализуется плавный ввод ковша в забой, при этом избегается чрезмерное заглубление ковша. В интервале «больше рабочего» реализуется та же стратегия отработки задания толщины стружки, однако качество отработки оказывается ниже, чем в рабочей области, поскольку управление более грубое, что вызвано необходимостью борьбы с вырыванием ковша из забоя в силу его естественных движений.

Наконец, третий алгоритмический блок — алгоритм управления приводом подъема. Это вспомогательный нечеткий алгоритм, призванњ\й улучшить качество отработки заданной толщины стружки. Он использует четыре лингвистические переменные: «частота вращения призоДа поДъема», «ошибка отработки задания», «высота зубьев ковша», «изменение ВЫХОДНОГО задания привоДу поДъема» и базу из 20 правил. Его задача увеличивать или уменьшать частоту вращения привода подъема, облегчая отработку задания приводу напора, при этом избегая остановки привода подъема.

Результаты моделирования процесса черпания довольно крепкой породы П-й категории с сопротивлением копанию 0.075*10 ⁶Па и уступа, имеющего угол 60 ⁰, приведены рис. 6.

Из рисунка видно, что время заполнения ковша составляет примерно 7 с, что является вполне приемлемым для экскаватора ЭКГ-15, что говорит в пользу работоспособности предложенного алгоритма.

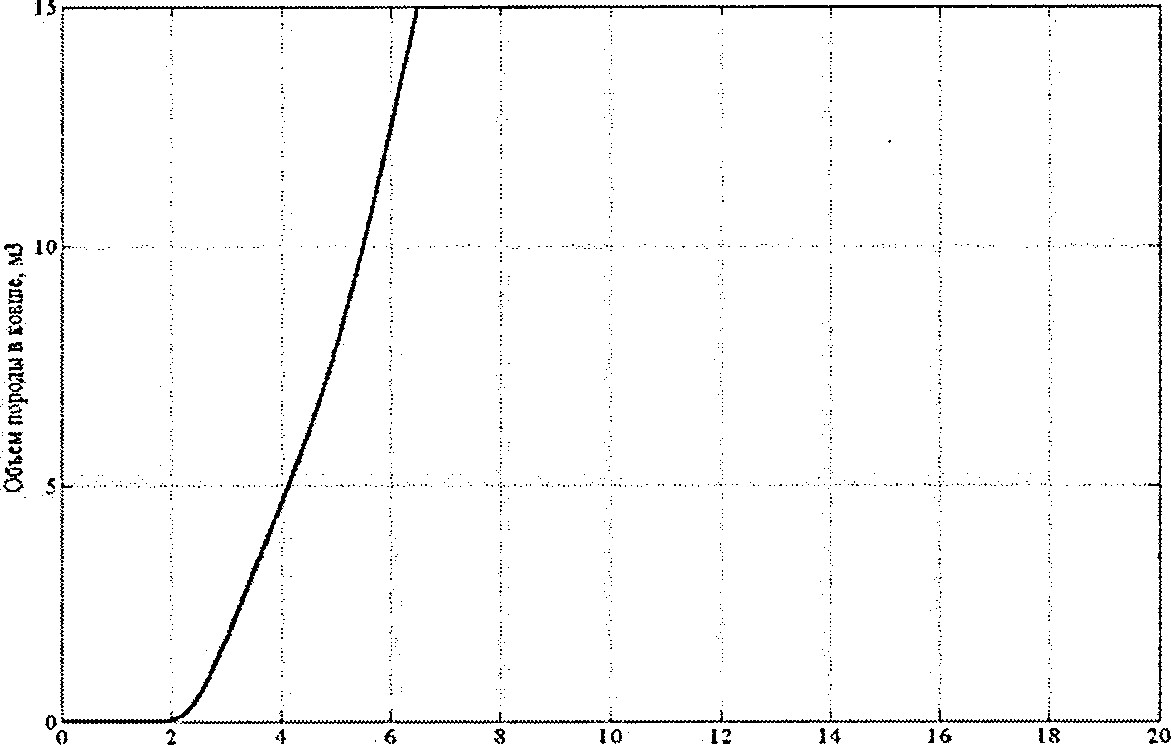
Модельное время. с

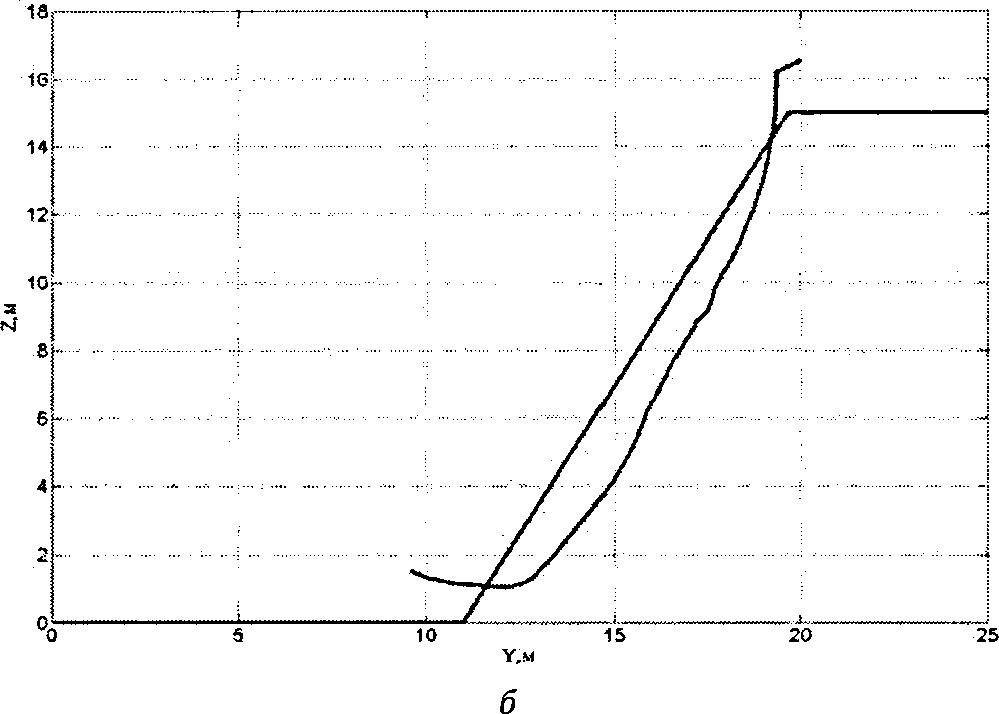
Рис.б. Оценка объема породы в ковше - а и траектория движения ковша в забое - б

В пятой главе приведены результаты решения задач практической реализации системы автоматизированного управления. В главе приводится структурная схема, реализующая концепцию трехрежимного управления, которая заключается в том, чтобы предоставить три способа управления эксикатором:

• ручное управление;

дистанционно-автоматическое управление;

автоматическое управление.

В ручном режиме управление ведется из кабины машиниста, при этом к полному сохранению работоспособности используемых на сегодняшний день органов управления добавляются средства отображения состояния главных и вспомогательных приводов и механизмов, а также параметров машины в целом.

Дистанционно-автоматический режим предполагает удаленное наблюдение и управление из отдельно стоящего диспетчерского пункта. На диспетчерском пункте продублированы все органы управления экскаватором. При помощи видеокамер и средств виртуальной реальности оператор видит происходящее в забое, и для него создается «эффект присутствия». В этом режиме доступно как полное ручное дистанционное управление, так и управление отдельными операциями технологического цикла, основная часть которого выполняется в автоматическом режиме. Такой способ управления достаточно широко используется на шахтах и рудниках в Канаде, Швеции, ЮАР. Основное достоинство такого способа

возможность управления с участием одного машиниста несколькими экскаваторами.

Третий способ управления — полностью автоматическое управление. В этом режиме все элементы цикла экскавации выполняется без участия оператора, но под его дистанционным наблюдением. Подобный режим применим для работы в типовых условиях, Оператор необходим деля разрешения ситуаций, когда, автоматический алгоритм выполнит переход в ручной режим, например при неудачном выводе ковша из стопорения.

В главе также приводится описание ядра бортовой части системы

специализированного вычислителя отечественной разработки ОАО «НИИВК им. М.А. Карцева» под кпзвашем «Жесткость» с характеристиками:

Процессор lntel Pineview-D 1.66 CJHz. (Dual core 0510);
ОЗУ DDR2 SDRAM 1024 Мбайт;
Поддержка интерфейсов: PCI-Express х 1, x16; SATA Н; Audio АС'97;

Gigabit Ethemet•, VGA, LVDS 18/36-бит;

Сторожевой таймер Watchdog;
Порты ввода/вывода RS485/RS422, САМ,
Навигационные модули Модуль Wi-Fi; совместимость с Dos, хр, хре, QNX 4.20, 6.0, Linux•, Наработка на отказ: 57000 часов.

Вычислитель имеет подпружиненный корпус, что позволяет располагать его на борту машины в горнотехнологических условиях карьера для реализации алгоритмов управления технологическими операциями экскаваторного цикла и вспомогательных программ.

При рассмотрении возможности использования результатов диссертационной работы ОАО «НИИВК им. М.А. Карцева» было установлено, что предложенные алгоритмы автоматического управления позволяют повысить эффективность использования карьерного экскаватора-мехлопаты на 1094.

ЗАКЛЮЧЕНИЕ

В настоящей диссертационной работе дано новое решение актуальной научной задачи автоматизации управления мощными карьерными экскаваторами, применяющимися в горнодобывающей промышленности, за счет разработки структуры и алгоритмов управления системы автоматического управления технологическими операциями экскаватора-мехлопаты, включающей алгоритмы управления операциями черпания и транспортирования горной массы.

Основные результаты диссертационной работы:

Разработан метод построения математической модели движения рабочего органа карьерного экскаватора-мехлопаты, базирующейся на сведении расчетной схемы экскаватора к схеме эквивалентного робота-манипулятора и применении к ней структурного подхода для описания роботов-манипуляторов.
Построена комплексная математическая модель движения рабочего органа и главных механизмов экскаватора ЭКГ-15 как объекта управления, пригодная для описания процессов, протекающих при выполнении экскаватором транспортных операций и операции черпания.

З. Предложен алгоритм управления транспортными движениями ковша экскаватора, базирующийся на применении комбинации системы управления обобщенными координатами экскаватора и решения обратной задачи определения координат экскаватора в зависимости от координат его ковша в базовой системе. Показана применимость данного алгоритма для отработки спланированной пространственно-временной траектории.

Разработан алгоритм управления операцией черпания с элементами нечеткой логики, включающий нечеткие алтритмы определения толщины снимаемой с забоя стружки и алгоритмы управления приводами напора и подъема для отработки заданной толщины стружки, а также алгоритм выхода из ситуации стопорения ковша. Выполнено моделирование работы предложенных алгоритмов, показавшее их работоспособность.
Разработана структура системы автоматическот управления операциями полного экскаваторного цикла, выполнены модельные исследования разработанных алгоритмов, которые обнаружили приемлемое качество управления при транспортировании и черпании.

Предложена структура аппаратного обеспечения системы автоматического управления технологическими операциями экскаватора-мехлопаты на основе бортового специализированного вычислителя.

ОСНОВНЫЕ ПОЛОЖЕНИЯ ДИССЕРТАЦИИ ОПУБЛИКОВАНЫ: в изДаниях по перечню ВАК Минобрнауки России:

Бабаков СЕ. Математическое моделирование динамики карьерного экскаватора на основе метода Белоусова. //«Вопросы радиоэлектроники». - 2012. вып. 2. -С. 112-118.
Певзнер Л.Д., Бабаков СЕ. Математическое модель динамики карьерного экскаватора как объекта управления. //«Мехатроника. Автоматизация. Управление.». - 2012. -№8. -с. 40-48.
Певзнер Л.Д., Бабаков СЕ. Управление операцией черпания карьерного экскаватора-мехлопаты с применением нечеткой логики. //<<Уголь». -2012. - №8. с.64-65.

4.Певзнер Л.Д., Бабаков СЕ. Алгоритмизация управления движением ковша экскаватора в режиме черпания с применением нечеткой логики. //«Горное оборудование и электромеханика». -2012. - №9. -С.8-17.

6 Других изДаниях:

5. Певзнер Л.Д., Бабаков СЕ. Моделирование динамики карьерного экскаватора как манипуляционного робота. [Сборник докладов ХХ международною научно-технического семинара «Современкше технологии в задачах управления, автоматики и обработки информации». (г.Алушта, 2011. ) С. 30-31.

Депонированные статьи:

1 .Певзнер Л.Д., Бабаков СЕ. Моделирование и управление операцией транспортирования экскаватора-мехлопаты. //Депонированная рукопись объемом 21 стр. издательства «Горная книга», справка № 917/08-12 от 22 мая 2012.

2.Певзнер Л.Д., Бабаков СЕ. Алгоритм управления операцией черпания карьерного экскаватора-мехлопаты с применением нечеткой логики. //Депонированная рукопись объемом 11 стр. издательства «Горная книга», справка № 920/09-12 от июня 2012.

Подписано в печать 25.09.2012. Формат 60х90/16

Объем печ. л. Заказ № 1403

Отдел печати МГГУ, Москва, Ленинский пр., 6