Курсовая работа Дорох. Разработка приложений на языке высокого уровня

• Название: Разработка приложений на языке высокого уровня
• Анкор: Курсовая работа Дорох
• Дата: 01.08.2022
• Размер: 2.67 Mb.
• Имя файла: Курсовая работа Дорох.docx
• Тип: Курсовая; #638745
• страница: 2 из 3

Содержание

Реферат 3

Введение 5

Нормативные ссылки 6

1Задача №1 7

1.1 Формулировка задачи 7

1.2 Спецификации задачи 7

1.3 Математическая постановка задачи 7

1.4 Описание вычислительных методов 7

1.5 Схема алгоритма. Описание 8

1.6 Текст программы и схема алгоритма 9

9

Рис. 4. Схема метода CheckNumbers 11

1.7 Ручной просчет отладочного варианта 11

1.8 Результаты машинного тестирования программы 12

1.9Инструкции пользователя 12

2Задача №2 13

2.1 Формулировка задачи 13

2.2 Спецификации задачи 13

2.3 Математическая постановка задачи 13

2.4 Описание вычислительных методов 14

2.5 Схема алгоритма. Описание 16

2.6 Текст программы и схема алгоритма 18

2.7 Ручной просчет отладочного варианта 24

2.8 Результаты машинного тестирования программы 24

2.9Инструкции пользователя 26

Заключение 27

Список использованных источников 28

Приложение 29

Введение

В процессе выполнения данной курсовой работы стояла задача создания двух программ на высокоуровневом языке программирования С#. Для их реализации потребовался практически весь опыт и все знания, накопленные за пройденный курс дисциплины «Языки программирования».

Для создания программ потребовались такие умения, как работа с консольными приложениями и Windows Forms, создание и грамотная реализация циклов, ветвлений, двумерных массивов и методов. Работа также требовала наличия определенных знаний в некоторых областях математики.

Язык С# является одним из наиболее востребованных современных языков программирования, при этом он достаточно прост для изучения и использования. Инструментарий С# позволяет решать множество разнообразных задач и создавать даже самые сложные и масштабные проекты. На нем разрабатывают:

Приложения для WEB;

Приложения для Android и IOS;

Программы для Windows;

Видеоигры и многие другие проекты.

Информационной базой исследования является учебная литература по программированию, техническая документация по языку C#, методические указания по выполнению курсовой работы.

Нормативные ссылки

В настоящей пояснительной записке используются ссылки на следующие нормативные документы:

ГОСТ 7.32-2001 «Отчет о научно-исследовательской работе. Структура и правила оформления».

ГОСТ 2.105-95 «Общие требования к текстовым документам»

ГОСТ Р 7.0.5-2008 «Библиографическая ссылка. Общие требования и правила составления»

ГОСТ 7.1-2003 «Библиографическая запись. Библиографическое описание. Общие требования и правила составления»

ГОСТ 7.80-2000. «Библиографическая запись. Заголовок. Общие требования и правила составления»

ГОСТ 19.701-80 – ЕСПД. Схемы алгоритмов, программ, данных и систем.

1. Задача №1

   1. 
      Формулировка задачи
      

Получить все четырехзначные натуральные числа, в записи которых нет двух одинаковых цифр. Вывести их в виде гистограммы.

2. 
   Спецификации задачи
   

Входные данные:

- Совокупность всех четырехзначных чисел от 1000 до 9999.

Выходные данные:

- Совокупность четырехзначных чисел, соответствующих условию, в виде гистограммы.

3. 
   Математическая постановка задачи
   

Необходимо вывести все четырехзначные числа, не имеющие повторяющихся цифр. Для этого нужно создать программу, которая распознает каждую отдельную цифру в числе и, в случае неравенства каждого из них между собой, выводит на экран число.

4. 
   Описание вычислительных методов
   

Программа должна принимать совокупность четырехзначных чисел и отдельно проверять каждое из них на наличие повторяющихся цифр. Для этой проверки необходимо разбить исходные числа на их составляющие, то есть на отдельные цифры, и сравнить их между собой.

В программе эти действия были реализованы с использованием операций деления целых чисел и деления с запоминанием остатка, а также элементов математической логики.

Сначала каждое новое поступившее число N делится операцией деления с запоминанием остатка на 10, тем самым запоминая только последнюю цифру числа. Затем исходное число целочисленно делится на 10, последняя цифра отбрасывается. Эти два действия повторяются до тех пор, пока не будет распознана каждая цифра числа. Таким образом получаем два уравнения (N – исходное число, a[x] – запоминаемая цифра):

a[x] = N % 10 (1)

N = N / 10 (2)

Они выполняются друг за другом количество раз, равное разрядности исходного числа N. Так происходит распознавание цифр в числе.

Остается провести проверку, которая определит, есть ли среди распознанных цифр повторяющиеся. Воспользуемся элементарной математической логикой и получим формулу (R – разрядность исходного числа):

a[x] == a[ 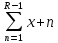] (3)

В программе эта формула применяется в виде цикла, который сначала берет x = 0 и после каждого перебора увеличивает x на 1. Таким образом, каждая цифра числа сравнивается с каждой другой. Если эта формула даст значение ИСТИНА хотя бы раз, то число не будет выведено на экран, в ином случае оно появится на экране.

5. 
   Схема алгоритма. Описание
   

В программе были использованы следующие структурные элементы: цикл for, ветвление через оператор if. Сначала с помощью оператора цикла for перебираем все четырехзначные числа, затем внутри него начинает свою работу еще один цикл for, содержащий формулы (1) и (2). Затем происходит вызов метода CheckNumbers внутри операции ветвления. Метод CheckNumbers работает по формуле (3): вызывается двойной цикл for, внутренняя часть которого отвечает за перебор всех чисел ряда из правой части уравнения, а внешняя – за перебор значений x.

Вывод в виде вертикальной линии происходит с использованием команды DrawLine внутри цикла, в ней задается цвет линии, а также координаты её начала и конца. Координата по X у каждой линии зависит только от самого числа и является одинаковой в начале и конце, то есть по “иксу” каждая линия занимает только один пиксел, координата Y же берёт свое начало у нижнего края окна вывода и имеет конец, зависящий от числа. Таким образом наглядно демонстрируется зависимость между высотой линии и размером числа. Так как программа выводит огромное количество чисел в виде линий, гистограмма была реализована так, чтобы полностью помещаться в окно вывода в ущерб точности гистограммы. По такому же принципу справа была реализована “линейка” для сравнения чисел.

Алгоритм обладает свойством массовости – при желании пользователь может сменить значения n1 и n2 для изменения границ диапазона выводимых цифр.

6. 
   Текст программы и схема алгоритма
   

Рис. 1. Текст программы для вывода чисел в виде гистограммы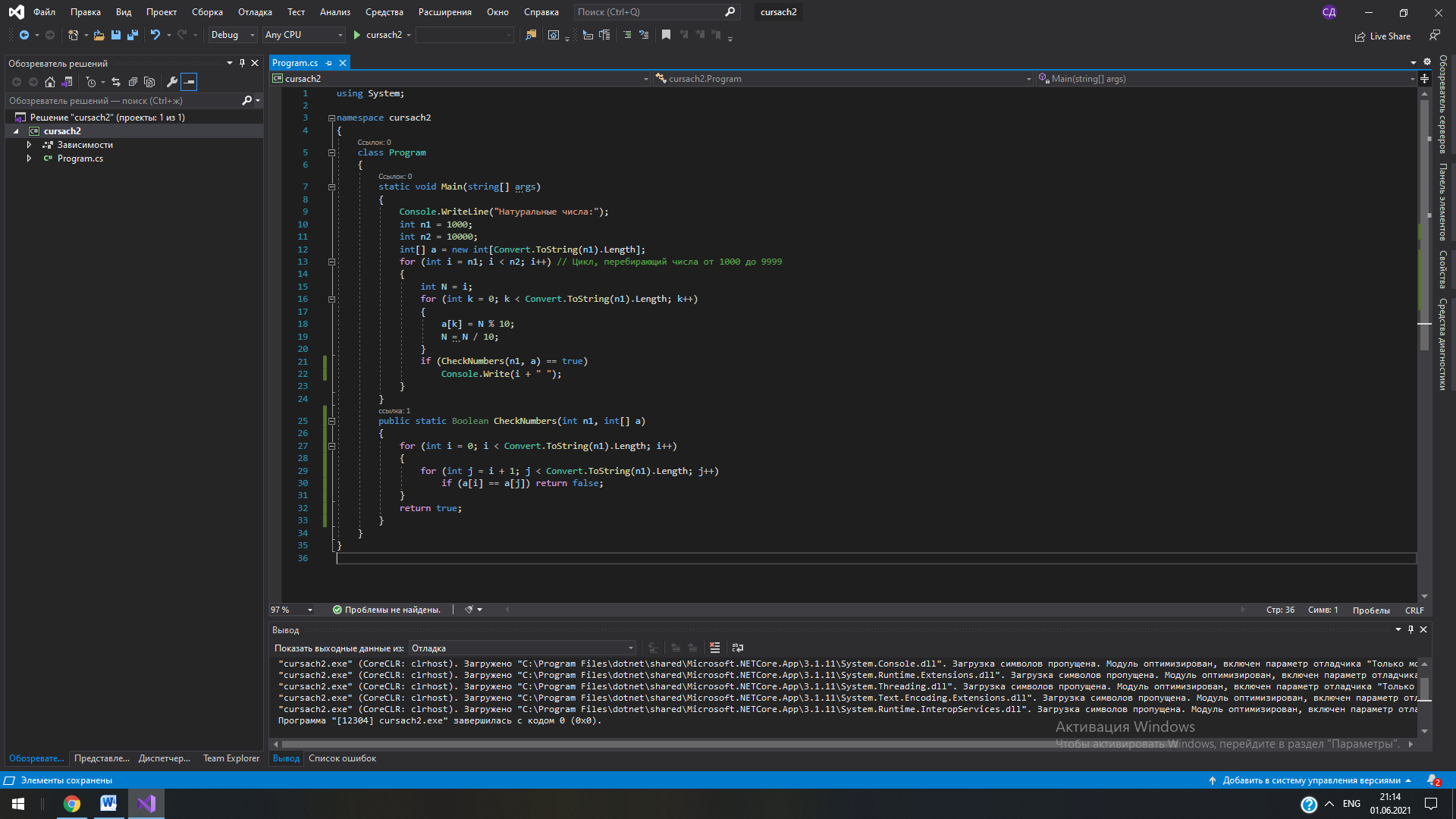



Рис. 2. Текст программы для вывода чисел в текстовом виде


Начало



n1, n2, a[]



i=n1; i


Вывод основной линии оси Y



N=i





k=0; k
i=1; i<=10; i++





a[k] = N % 10; N = N / 10;

Вывод горизонтальных линий на оси Y





CheckNumbers=true

Вывод чисел на оси Y



Да

Нет



Конец



Рис. 3. Схема алгоритма

Вывод i

CheckNumbers

i=0; i

a[i] == a[j]

j=i+1; j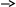

Нет

Да

Возврат true

Возврат false

Рис. 4. Схема метода CheckNumbers

7. 
   Ручной просчет отладочного варианта
   

Для просчета возьмем любое четырехзначное число, например, 1623.

a[0] = 1623 % 10 = 3; 1623/10 = 162;

a[1] = 162 % 10 = 2; 162/10 = 16;

a[2] = 16 % 10 = 6; 16/10 = 1;

a[3] = 1 % 10 = 1; 1/10 = 0;

Как видно, все найденные цифры совпадают с соответствующими цифрами в числе. Повторяющихся цифр нет, следовательно число 1623 будет выведено на экран.

8. 
   Результаты машинного тестирования программы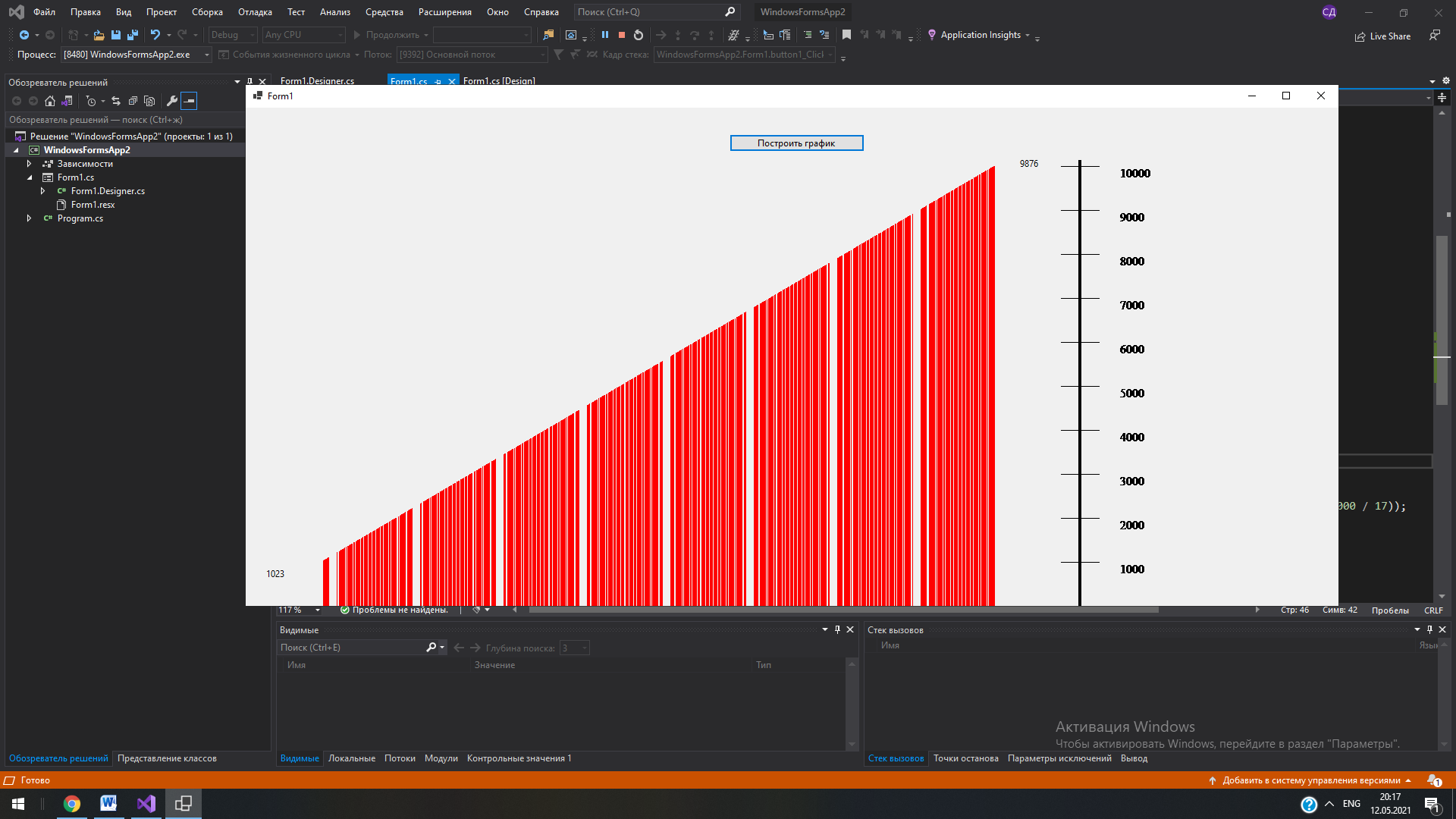
   

Рис. 5. Результаты выполнения программы. Гистограмма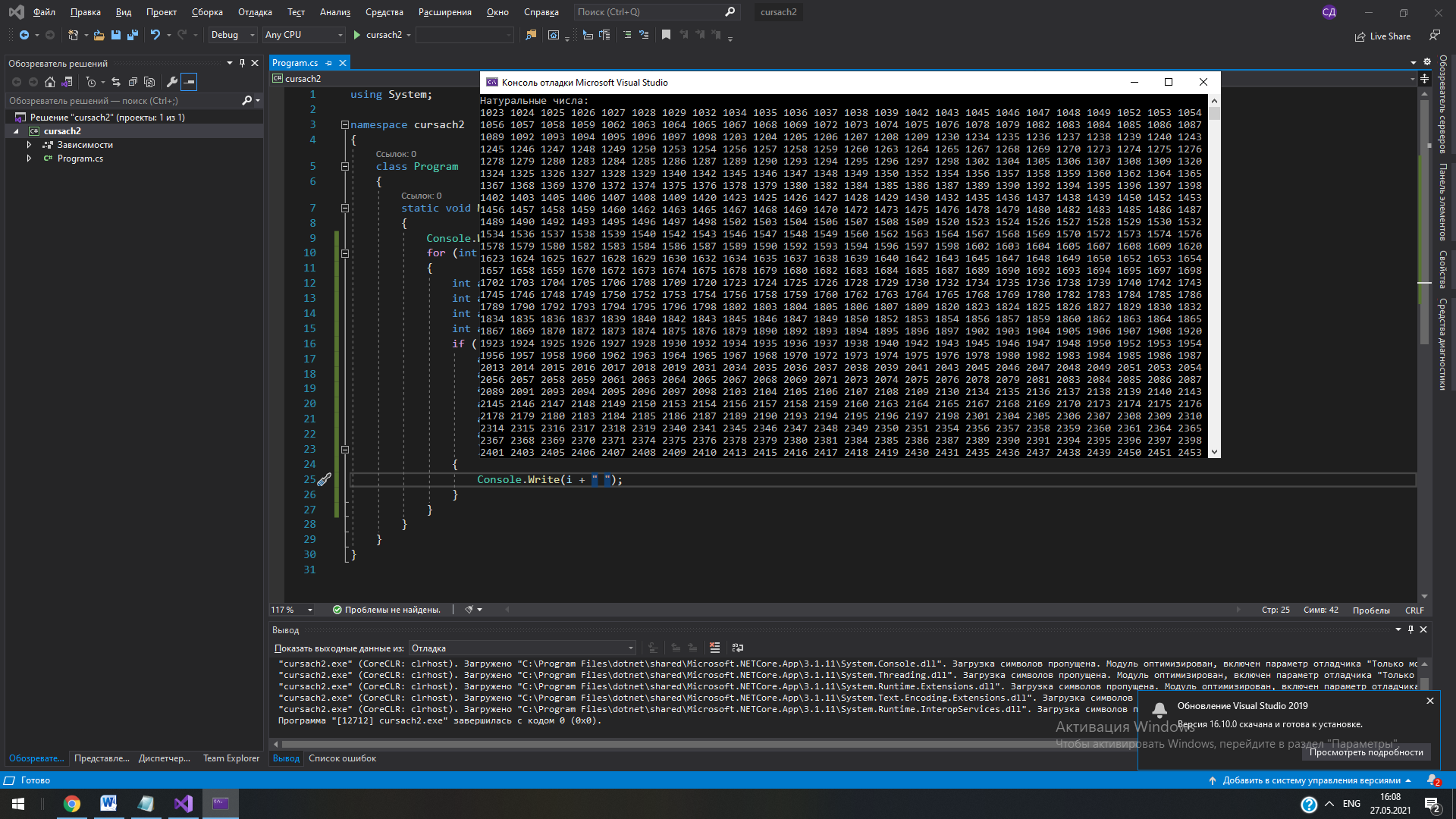



Рис. 6. Результаты выполнения программы. Вывод чисел

9. 
   Инструкции пользователя
   

Для построения гистограммы пользователю требуется нажать на кнопку “Построить график” в окне вывода. На экране появятся все числа без повторяющихся цифр в виде вертикальных красных линий и линейка для сравнения их между собой. Пользователь также может задать границы диапазона выводимых чисел, изменив значения n1 и n2.

2. 
   Задача №2
   
   1. 
      Формулировка задачи
      

Даны четыре матрицы размера m*n. Если элементы, стоящие на одинаковых позициях в этих матрицах, равны – поместить их в новую матрицу на соответствующие позиции. Остальные элементы новой матрицы приравнять к нулю. Найти определитель новой матрицы.

2. 
   Спецификации задачи
   

Входные данные:

- Размерность матриц m x n.

- Исходные матрицы A, B, C и D.

Выходные данные:

- Новая матрица, полученная путем копирования одинаковых элементов исходных матриц, стоящих на одинаковых позициях, и обнуления всех остальных элементов.

- Определитель новой матрицы.

3. 
   Математическая постановка задачи
   

Для решения задачи необходимо создать программу, принимающую значения m и n и использующую их для задания размерности матриц. Затем пользователь должен записать значения всех элементов исходных четырех матриц (A, B, C, D). Программа же должна вывести новую матрицу E, полученную в соответствии с условиями задачи, и её определитель. В таблице 1 представлены переменные, используемые в программе.

Таблица 1

Характеристика переменных

Имя переменной	Смысл переменной	Назначение переменной
M	Целое число строк	Исходная
N	Целое число столбцов	Исходная
A[,]; B[,]; C[,]; D[,]	Исходные матрицы	Исходные
E[,]	Новая матрица	Результат
Det	Определитель новой матрицы	Результат
minor[,]	Минор матрицы	Промежуточная
Sign	Знак минора	Промежуточная

4. 
   Описание вычислительных методов
   

Как известно, матрица представляет собой прямоугольную таблицу элементов, состоящую из строк и столбцов. Пользователь заполняет четыре матрицы произвольной размерности любыми элементами. Программа считывает эти матрицы и переносит одинаковые элементы с одинаковых позиций в новую матрицу. Если же элементы не совпадают, то в новой матрице на этой позиции будет стоять нуль.

Следующей целью задания является нахождение определителя полученной матрицы. В программе был реализован алгоритм нахождения определителя матрицы любой размерности через миноры.

Для нахождения определителя матрицы размерностью 2x2 была использована формула: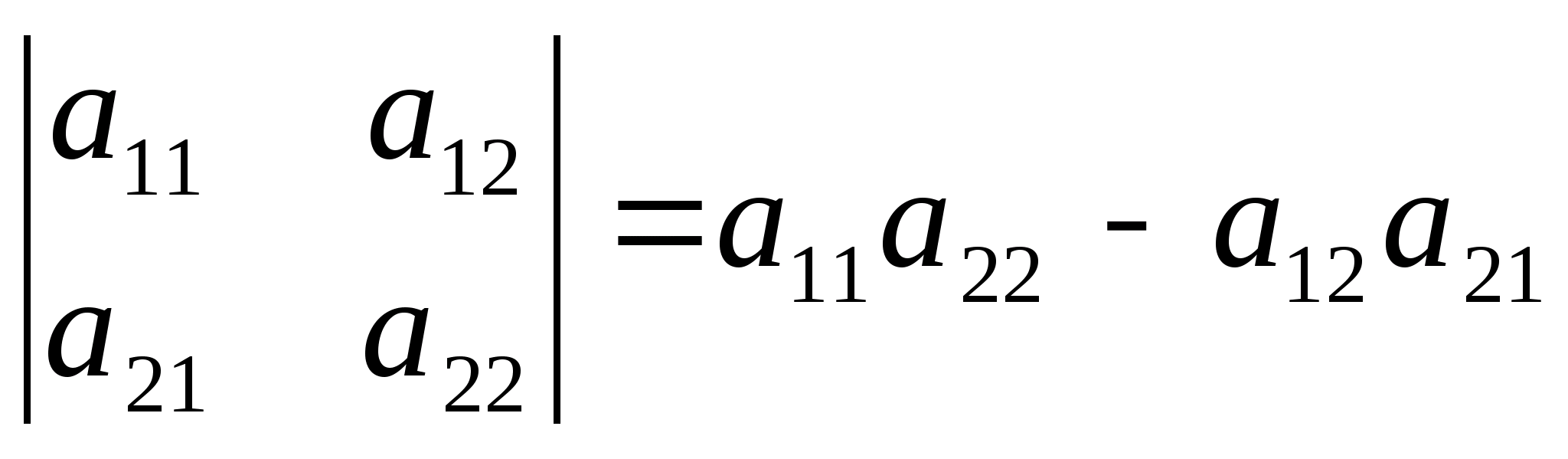

(4)

Для нахождения определителя матриц с большей размерностью применяется метод разложения на миноры. Это разложение повторяется до тех пор, пока очередной минор не достигнет размерности 2x2, тогда к нему можно будет применить формулу (4). Рассмотрим формулу: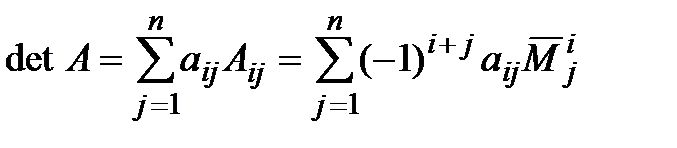

(5)

Эта формула является основной при решении задачи. Здесь a_ij – элемент, стоящий на соответствующей позиции, а А_ij – алгебраическое дополнение этого элемента, которое находится как минор элемента, взятый со знаком “минус”, если сумма номеров строки и столбца, на пересечении которых стоит элемент, является нечетной, и со знаком “плюс”, если четной. Минор, в свою очередь, это определитель матрицы, полученной путём вычеркивания из исходной матрицы строки и столбца, находящихся на пересечении элемента. Таким образом, для нахождения определителя матрицы необходимо умножить все элементы произвольного ряда на их алгебраические дополнения, после чего всё это сложить.

Для нахождения определителей матриц с большими размерностями необходимо многократно вычислять миноры первого элемента до тех пор, пока очередной из них не будет иметь размерность 2x2, так как определитель такой матрицы очень легко вычисляется. Найдя минор элемента матрицы 3x3, стоящего на позиции [0,0] и вычислив его, программа начинает обратно “разворачивать” матрицы, рассматривая уже второй элемент матрицы 3x3, а затем третий. После этого программа переходит уже ко второму элементу матрицы 4x4 и так далее. Такое решение понятно и легко реализуется, но его минус заключается в том, что при вычислении определителей матриц с очень большими размерностями компьютер будет перегружен огромным количеством операций.

5. 
   Схема алгоритма. Описание
   

Первым делом при запуске программы пользователя просят ввести количество строк m и столбцов n в матрицах. Оператор if проверяет введенные значения, и, если любое из них меньше одного, программа выводит сообщение об ошибке и закрывается.

В ином случае выполнение алгоритма продолжается. Инициализируются 5 двумерных массивов размерностью m x n. Это и есть матрицы. Для каждой из матриц A, B, C, D вызывается метод Vvod, позволяющий ввести с клавиатуры все элементы. Метод работает на основе перебора всех элементов и использует для этого вложенные циклы. Если пользователь введет символ неверного формата, вместо него в матрицу будет записана цифра 0. Для вывода введенных матриц на экран вызывается метод Vivod. Он работает по тому же принципу, но вместо ввода данных он лишь выводит на экран полученные матрицы.

Далее с помощью тех же вложенных циклов for программа перебирает все позиции элементов матриц построчно и сравнивает между собой элементы массивов A, B, C и D, стоящих на одной и той же позиции. Для этого сравнения используется оператор ветвления if. Если все элементы оказываются равны, это значение записывается в новую матрицу E на ту же позицию. Иначе значение элемента на этой позиции в матрице E становится равно 0. В этом же цикле происходит и вывод всей полученной матрицы E.

Остается вычислить определитель матрицы E. Программа вновь прибегает к ветвлению, на этот раз для того, чтобы определить, правильную ли размерность имеет матрица. Если число строк m не равно числу столбцов n (т. е. матрица не квадратная), то программа выводит сообщение о невозможности нахождения определителя и завершает работу.

В ином случае вызывается метод Determinant, который возвращает целое число и записывает его в переменную det. Работает он следующим образом: оператором ветвления if определяется, имеет ли матрица размерность 2x2. Если да, то производится вычисление по формуле (4), после чего значение возвращается в метод Main. Если матрица имеет большую размерность, то затем вводятся переменные sign=1, которая используется для определения знака минора, и result=0, куда и будет записываться вычисленный определитель. Далее с помощью цикла for программа перебирает все элементы первого ряда матрицы, внутри этого цикла происходит 3 действия: сначала вызывается метод GetMinor, принимающий текущее значение счетчика (в этом методе он будет иметь название n) и матрицу, затем применяется формула (5), где снова используется вызов метода Determinant, но на этот раз он принимает только что вычисленный минор матрицы. Таким образом создается рекурсия метода Determinant. Третье действие – смена знака у переменной sign, как того требует та же формула (5).

Метод GetMinor, в свою очередь, сначала создает новую матрицу на основе принятой, задает ей размерность на 1 меньше. Затем с помощью вложенных циклов for происходит перебор всех элементов минора. Перебор переменной i начинается с единицы, а j – с нуля. Вводится ещё одна вспомогательная переменная col=0. Если j=n, то программа выходит из внутреннего цикла, так как нам не нужно включать в минор элементы, стоящие на пересечении с исходным элементом. Иначе программа присваивает элементу [i-1;col] созданного минора значение элемента E[i;j] исходной матрицы, после чего увеличивает значение col на 1. После завершения циклов полученный минор возвращается в метод Determinant, который по окончании своей работы возвращает в метод Main вычисленное значение определителя, это значение записывается в переменную det и выводится на экран.

6. 
   Текст программы и схема алгоритма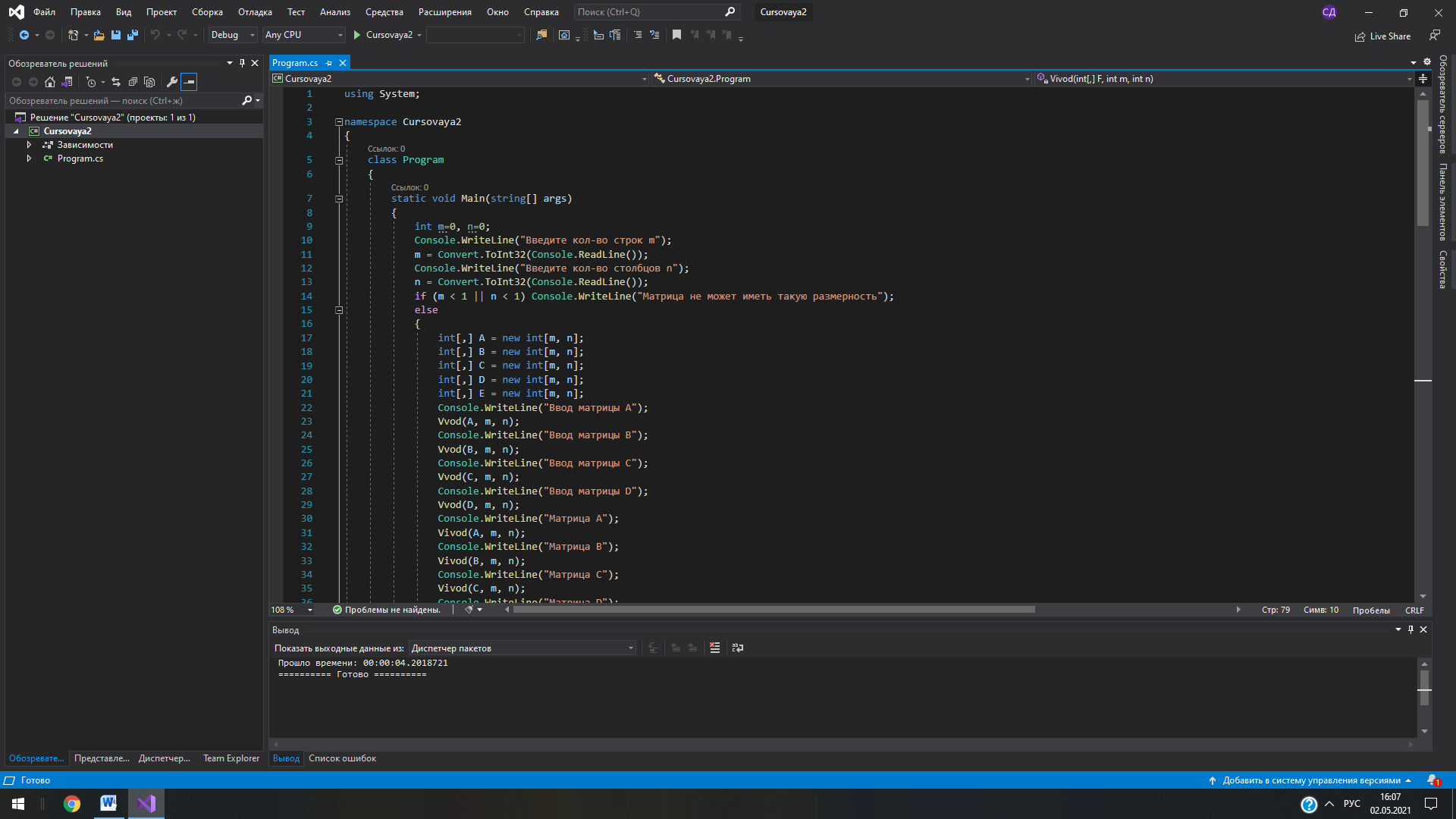
   

Рис. 7. Метод Main, основная часть программы (ч.1)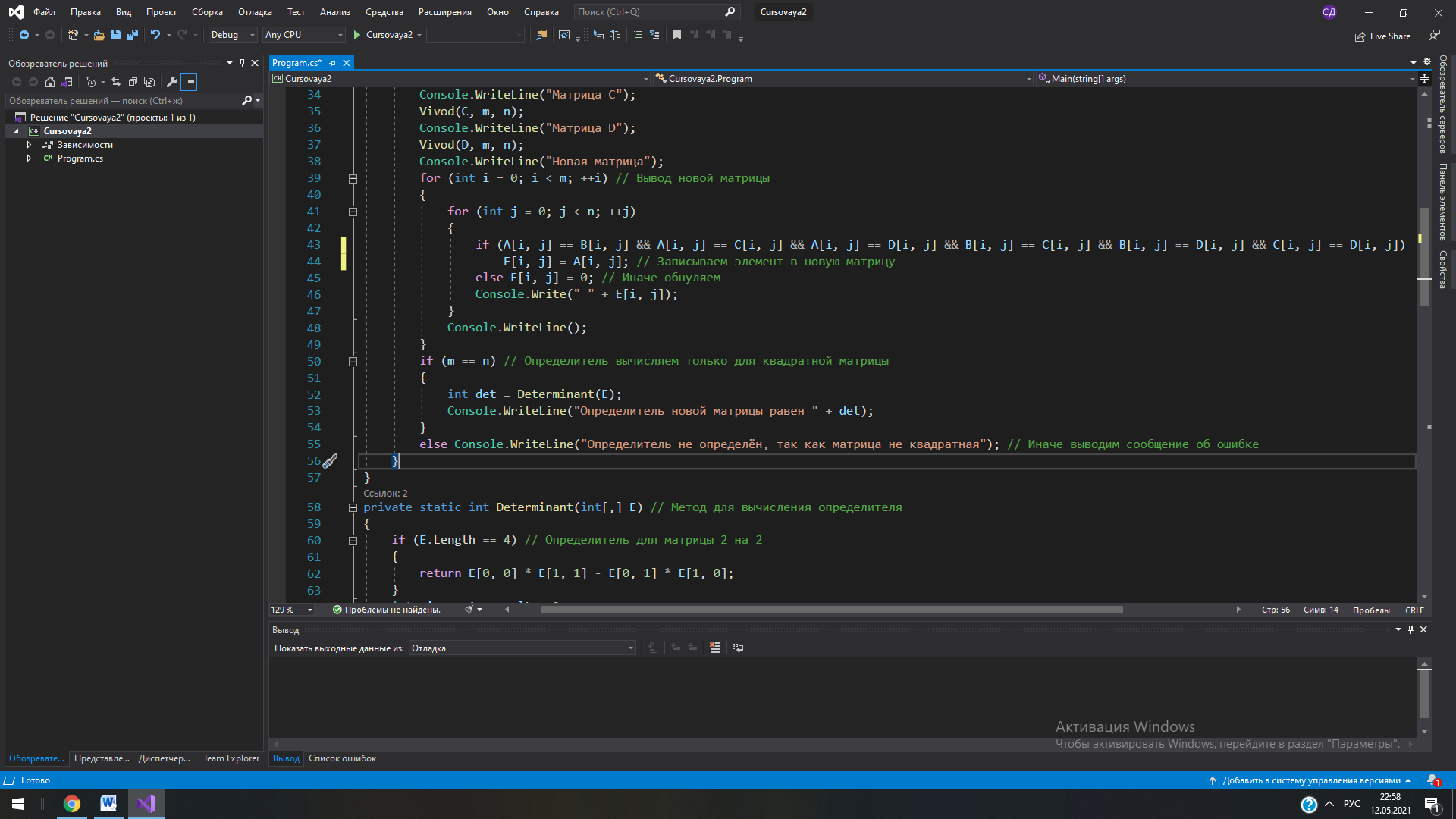



Рис. 8. Метод Main, основная часть программы (ч.2)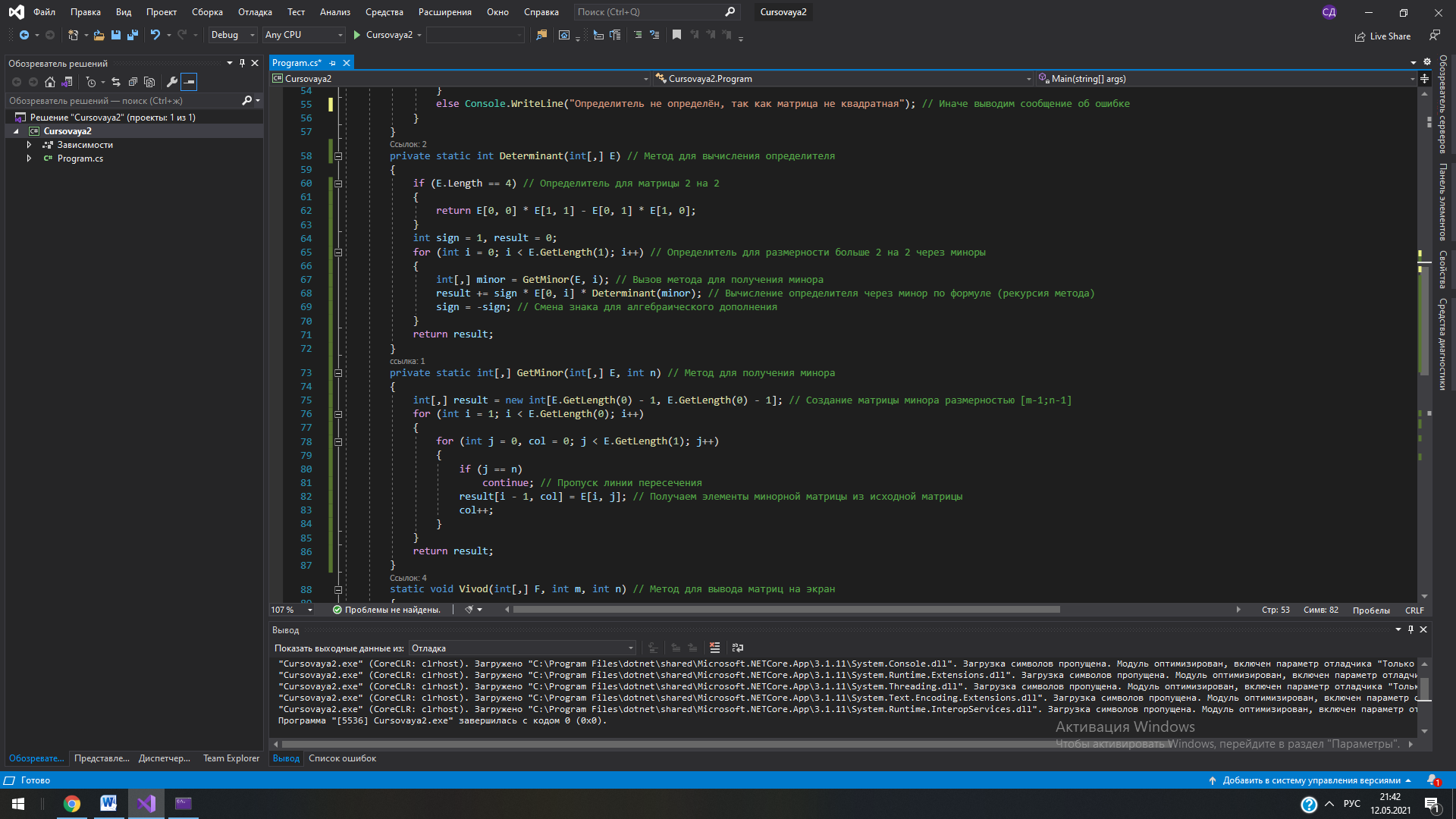



Рис. 9. Метод Determinant, вычисляющий определитель, и связанный с ним метод GetMinor, вычисляющий минор матрицы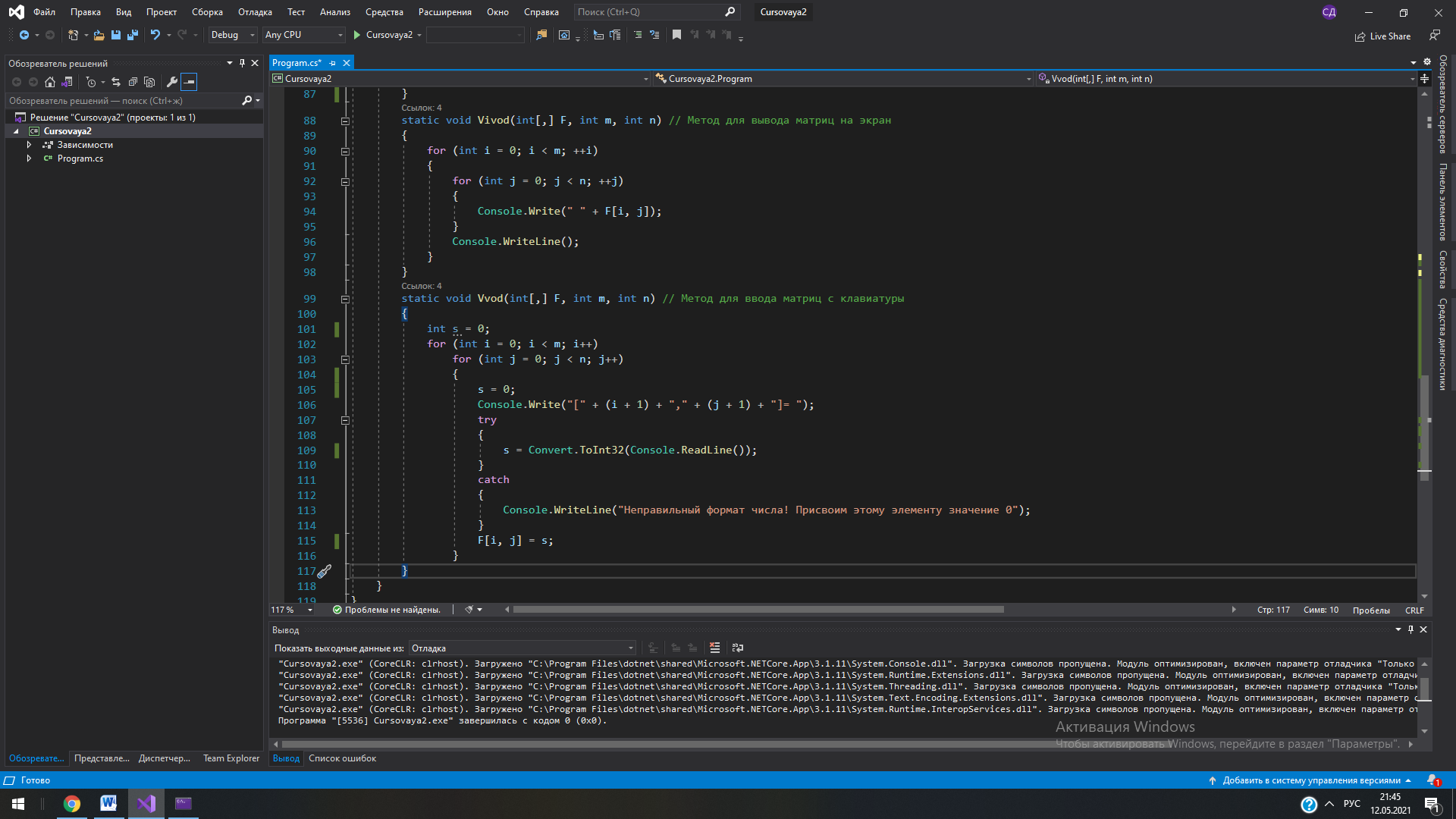



Рис. 10. Методы Vvod и Vivod, позволяющие вводить матрицы с клавиатуры (Vvod) и выводить их на экран (Vivod)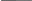

Да

Да

Нет

A[i,j]=B[i,j]=C[i,j]=D[i,j]

int j = 0; j < n; ++j

int i = 0; i < m; ++i

Ввод m, n

Начало



Инициализация массивов A, B, C, D, E размерностью [m,n]





Да

Нет

m < 1 || n < 1?

Метод Vivod для A

Метод Vvod для A





Метод Vivod для B

Метод Vvod для B



Вывод сообщения об ошибке

Метод Vivod для C

Метод Vvod для C



Метод Vivod для D

Метод Vvod для D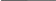







Вывод ошибки

Метод Determinant для E

m=n?

Рис. 11. Схема алгоритма

Конец

Нет

Вывод E[i,j]

E[i, j] = 0

E[i, j] = A[i, j]



Determinant



Да

Нет



E.lenght = 4?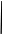







Возврат E[0,0] * E[1,1] – E[0,1] * E[1,0]

sign = 1; result = 0





int i = 0; i < E.GetLength(1); i++







minor = GetMinor





result += sign * E[0, i] * Determinant(minor)





sign = -sign





Возврат result







Выход


Рис. 12. Схема метода Determinant, вычисляющего определитель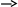

Vvod

F[i, j] = str

Ввод str с клавиатуры

int j = 0; j < n; ++j

int i = 0; i < m; ++i

str=0, F[i,j], m, n













Выход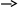



Вывод F[i,j]

int i = 0; i < m; ++i

int j = 0; j < n; ++j

F[i,j], m, n

Vivod
Рис. 13. Схема метода Vvod для ввода значений










Выход


Рис. 14. Схема метода Vivod для вывода матриц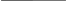


GetMinor

Инициализация массива result [m-1,n-1]

int i = 1; i < E.GetLength(0); i++

Рис. 15. Схема метода GetMinor для получения минора матрицы

Возврат result

Да

Нет

col++

result[i - 1, col] = E[i, j]

j=n?

int j = 0, col = 0; j < E.GetLength(1); j++

7. 
   Ручной просчет отладочного варианта
   

Посчитаем определитель матрицы 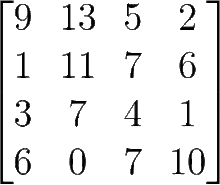воспользовавшись формулой, описанной ранее. det = a₁₁M₁₁ - a₁₂M₁₂ + a₁₃M₁₃ - a₁₄M_14.

М₁₁ = 11*4*10+7*7*6+7*1*0 - (6*4*0+7*7*10+11*7*1) = 167

М₁₂ = 1*4*10+3*7*6+7*6*1 - (6*4*6+7*1*1+3*7*10) = -153

М₁₃ = 1*7*10+3*0*6+6*11*1 - (6*7*6+0*1*1+3*11*10) = -446

М₁₄ = 1*7*7+6*11*4+3*0*7 - (6*7*7+1*4*0+3*11*7) = -212

Итого получаем: det = 9*167 + 13*153 + 5*(-446) + 2*212 = 1686

8. 
   Результаты машинного тестирования программы
   

Рис. 16. Результаты тестирования программы. Ввод матриц A и B



Рис. 17. Результаты тестирования программы. Ввод матриц C и D


Рис. 18. Результаты тестирования программы. Вывод всех матриц и определителя

9. 
   Инструкции пользователя
   

Пользователю необходимо сначала ввести количество строк и столбцов в матрицах. Затем нужно заполнить матрицы произвольными цифрами, начиная с матрицы A и до матрицы D. Заполнение происходит построчно слева направо. Если был введен символ неверного формата (например буква), то вместо него в матрицу вписывается нуль. После этого на экран выводится новая полученная матрица и её определитель. Если матрица не является квадратной, вместо этого на экране появится сообщение, указывающее на невозможность вычисления определителя для матрицы такой размерности.

Системными требованиями для запуска обеих представленных в курсовой работе программ являются:

ОС Windows 7 / 8 / 10 (32 / 64 bit);

Процессор с тактовой частотой не ниже 1,8 ГГц;

2 ГБ ОЗУ (Рекомендуемая 8 ГБ);

Для запуска программ необходимо сначала открыть соответствующие файлы с расширением .sln, в открывшемся окне нажать комбинацию клавиш Ctrl + F5.