Контрольная работа- Математика. Дифференциальные уравнения. Интегральные исчисления.. кр1. Контрольная работа 1 Вариант 7 Задание найти неопределенные интегралы. 1 Пусть u Тогда du подставим
 Скачать 42.31 Kb. Скачать 42.31 Kb.
|
|
Контрольная работа №1 Вариант 7 Задание: найти неопределенные интегралы. 1) 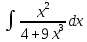 Пусть u= 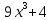 Тогда du= 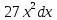 подставим подставим 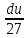 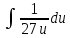 = =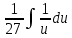 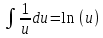 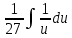 = =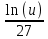 = =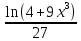 = =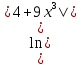 2) 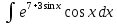 Пусть u=3sinx+7 Тогда пусть du=3cos(x)dx , подставим 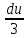 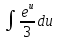 интеграл от экспоненты есть он же сам интеграл от экспоненты есть он же сам 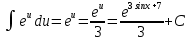 3) 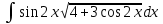 Выражение –sin(2x) подведем под знак дифференциала (-sin(2x)dx= d(cos(2x)) t=cos(2x) 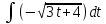 Замена переменных t=3x+4 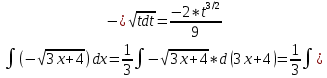 Возвращаемся к x 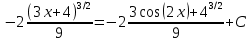 4) 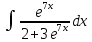 Пусть u= 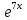 Тогда пусть du= 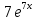 , подставим du: , подставим du: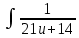 Пусть u=21u+14 Тогда пусть du=21 и подставим 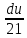 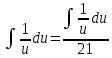 интеграл интеграл 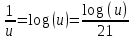 Произведем замену u: 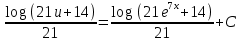 5) 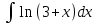 Сделаем замену переменных T=x+3 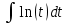 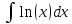 U=ln(x) Dv=dx Тогда Du= 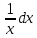 V=x Поэтому 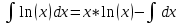 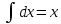 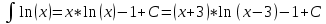 6) 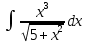 d= 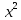 , t= , t=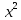 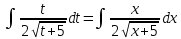 Делаем замену переменных 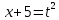 Следовательно 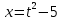 Dx=2t dt 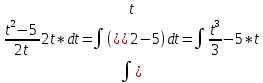 Подствим вместо t= 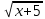 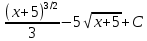 Подставим вместо x= 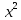 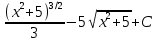 7) 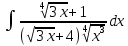 Делаем замену x= 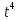 , тогда dx= , тогда dx=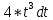 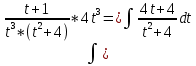 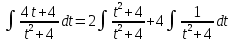 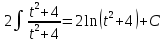 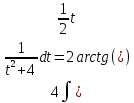 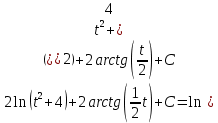 Подставим вместо t= 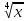 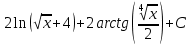 8) 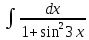 Пусть u=3x Тогда пусть du=3, подставим du: 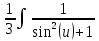 Вычисляем 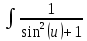 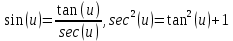 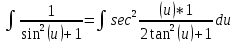 V=tan(u) Тогда пусть du= 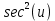 , подставим du: , подставим du: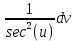 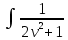 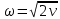 Тогда пусть dv= Тогда пусть dv=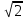 , подставим dv: , подставим dv: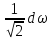 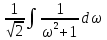 Вычисляем: 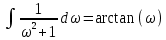 Подставляем вычисленные интегралы 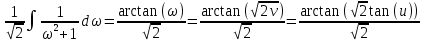 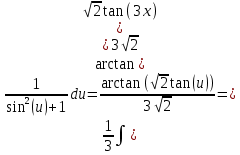 9) 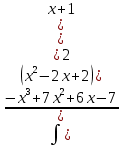 Разложим дробь на простейшие 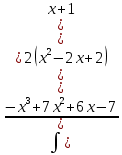 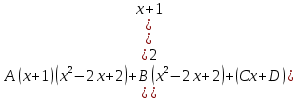 Приравняем числители и учтем, что коэффициенты при одинаковых степенях x, стоящие слева и справа должны совпадать: 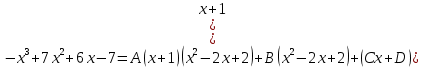 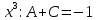 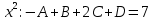 1: 2A + 2B + D = -7 x: -2B + C + 2D = 6 A = -3; B = -1; C = 2; D = 1 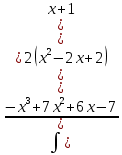 Вычисляем табличный интеграл: 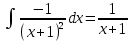 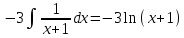 Раскладываем рациональную дробь на простейшие дроби: 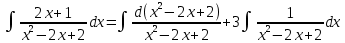 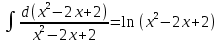 Вычисляем интеграл: 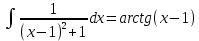 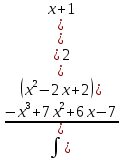 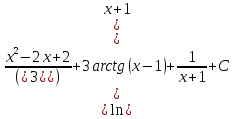 Задание: вычислить определенные интегралы. 10) 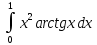 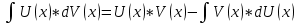 U=arctg(x) 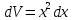 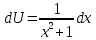 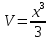 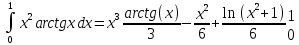 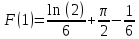 F(0)=0 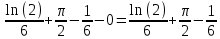 11) 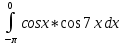 Применим формулы преобразования произведения функций: 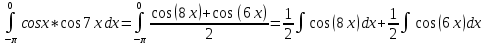 Вычисляем 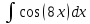 U=8x тогда du=8, подставим du: 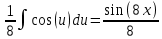 Вычисляем 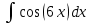 U=6x тогда dx=6du, подставим: 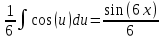 Подставим уже вычисленные интегралы: 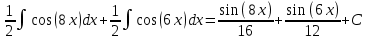 Задание: Вычислить несобственные интегралы или установить их расходимость 12) 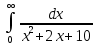 Выделим полный квадрат 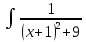 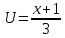 тогда dx=3du, подставим: тогда dx=3du, подставим: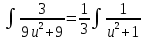 Вычисляем 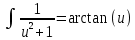 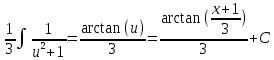 13) 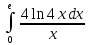 U=ln4x 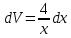 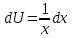 V=4ln(x) 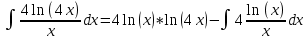 Находим интеграл 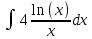 U=ln(x) 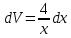 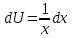 V=4ln(x) 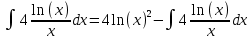 Находим интеграл 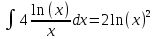 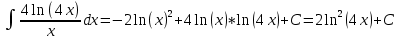 16)Нашли площадь области, ограниченной линиями 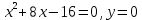 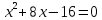 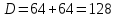 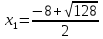 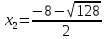 Точки A( 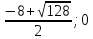 ) B( ) B(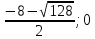 ) )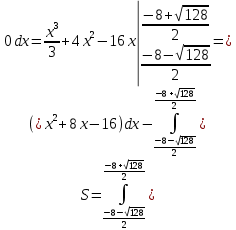 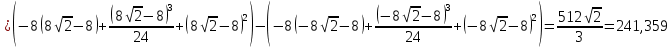 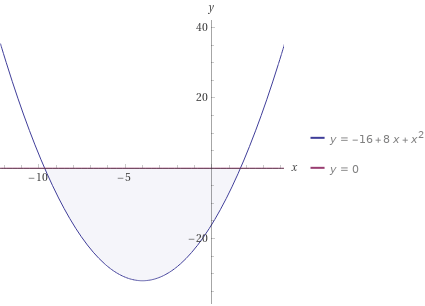 17)Нашли длину дуги кривой 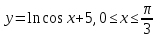 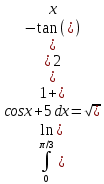 |
