Бакаленко. Разработка расходомера переменного перепада давлений и определение его метрологических характеристик
 Скачать 1.89 Mb. Скачать 1.89 Mb.
|
2.2 Оценка погрешности косвенных измеренийИзмерение расхода и само получение результата является косвенным измерением. В соответствии с методикой, косвенные измерения могут быть коррелированными и некоррелированными. Рассмотрим те случаи, когда корреляция отсутствует: При линейной зависимости и отсутствии корреляции между погрешностями измерений аргументов: Искомое значение А связано с m измеряемыми аргументами а1, а2, ..., аm уравнением:  где b - постоянные коэффициенты при аргументах a соответственно. Корреляция между погрешностями измерений аргументов отсутствует. Результат косвенного измерения А’ вычисляют по формуле:  где 16 Среднее квадратическое отклонение результата косвенного измерения S (А) вычисляют по формуле: где S( При нелинейной зависимости и отсутствии корреляции между погрешностями измерений аргументов: Для косвенных измерений при нелинейных зависимостях и некоррелированных погрешностях измерений аргументов используют метод линеаризации. Метод линеаризации предполагает разложение нелинейной функции в ряд Тейлора. Результат измерения А’ вычисляют по формуле:  Среднее квадратическое отклонение случайной погрешности результата косвенного измерения S (А) вычисляют по формуле: 2.3 Неопределенности измеренийВ 1993 году Международной Организацией по Стандартизации (ИСО) было разработано «Руководство по выражению неопределенности измерений». В результате этого собрания был осуществлён отказ использования понятия «погрешность» в пользу понятия «неопределенность». Таким образом, случайная погрешность приравнивалась к неопределённости типа А. Систематическая же погрешность отражалась неопределённостью типа В. Для неопределенности типа А стандартная неопределенность – неопределенность результата измерений, выраженная как среднеквадратичное отклонение (СКО). Для оценки неопределенности типа В необходима дополнительная информация: предварительные данные измерений; свойства материалов и приборов, относящиеся к измерениям; вид распределения и др. Оценка погрешности нашего расходомера находится по ГОСТ 8.586.52005 [3] (пункт 10.2). Формула содержит несколько составляющих, которые являются неопределённостями. С другой стороны, погрешность можно определить с помощью уравнения расхода: - уравнение расхода содержит 5 множителей ε, α, ρ1/2, d2, Δp1/2, от погрешностей которых зависит погрешность измерения расхода Qm или Qo. Имеются в виду случайные погрешности перечисленных величин. Систематические погрешности должны быть устранены или же учтены соответствующими поправками. Если были бы известны средние квадратичные случайные погрешности, то на основании закона сложения средних погрешностей можно записать: σQ = [σα2 + σε2 + (2σd)2 + (σρ2)2 + (σΔp2)2]0,5 (2.6) Класс точности СИ — обобщенная характеристика средств измерений, определяемая пределами допускаемых основной и дополнительной погрешностей, а также другими свойствами средств измерений, влияющими на их точность, значения которых устанавливаются в стандартах на отдельные виды средств измерений   3 Разработка расходомера с СУ 3 Разработка расходомера с СУ 3.1 Расчет диаметра СУ Расчет диаметра отверстия сужающего устройства и измерительного трубопровода в рабочих условиях производится согласно ГОСТ 8.586.1-2005 [1] где где Значения температурного коэффициента линейного расширения для различных материалов рассчитывают по формуле (3.3), приведенной в приложении Г, ГОСТ 8.586.1-2005 [1]. где Для Ст20: 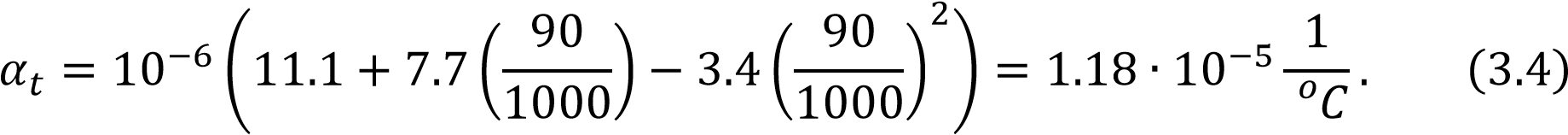 Подставим формулу (3.2) в формулу (3.1) и подставив численные значения получим: Расчет диаметра отверстия СУ выполняется согласно ГОСТ 8.586.1-2005 [1] приложение В.3. Необходимы следующие исходные данные: D, По условию задана влажность воздуха 40%, поэтому плотность будет расчитана по ГОСТ OIML R 111-1-2009 приложение Е [7] где p = 601325 Па; Ma = 0.0289635 кг/моль – молярная масса сухого воздуха; R = 8.314 Дж/(К*моль) – молярная газовая постоянная; T = 363.15 К – термодинамическая температура по МТШ-90; Xv = 0.048 кг/моль – молярная масса водяного пара; Mv = 18.01528*10-3 кг/моль – молярная масса воды. Z = 1.000023 Па-1 – сжимаемость; Подставив эти значения в формулу (3.6) получила плотность Массовый расход 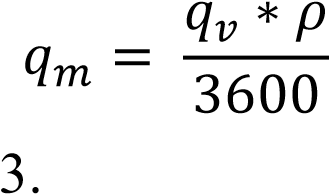 . . где Подставляя исходные данные, получаю максимальное значение массового расхода: Минимальное значение массового расхода: Проверяют выполнение неравенства:  Условия выполняются. Далее рассчитывают значения верхней границы Remax и нижней границы Remin рабочего диапазона значений числа Рейнольдса по формуле: где Подставляя, полученные значения массового расхода в формулу (3.11), получила верхнюю границу Remax: Нижняя граница Remin:  Значение числа Re должно быть более 5000. Затем рассчитывают значение вспомогательной величины А по формуле  Подставив значение перепада (75000 Па) в формулу (3.15) найдём величину А:  Из пункта 5.3.1 ГОСТ 5.586.2 [2] определяют значения верхней границы относительного диаметра βв и нижней границы βн: Рассчитывают значения вспомогательных величин B1 и B2 по формулам: где E1,2 – коэффициенты скорости входа при С1 – коэффициент истечения при Remax и С2 – коэффициент истечения при Remin и Коэффициенты истечения С1, С2, которые определяются следующими уравнениями 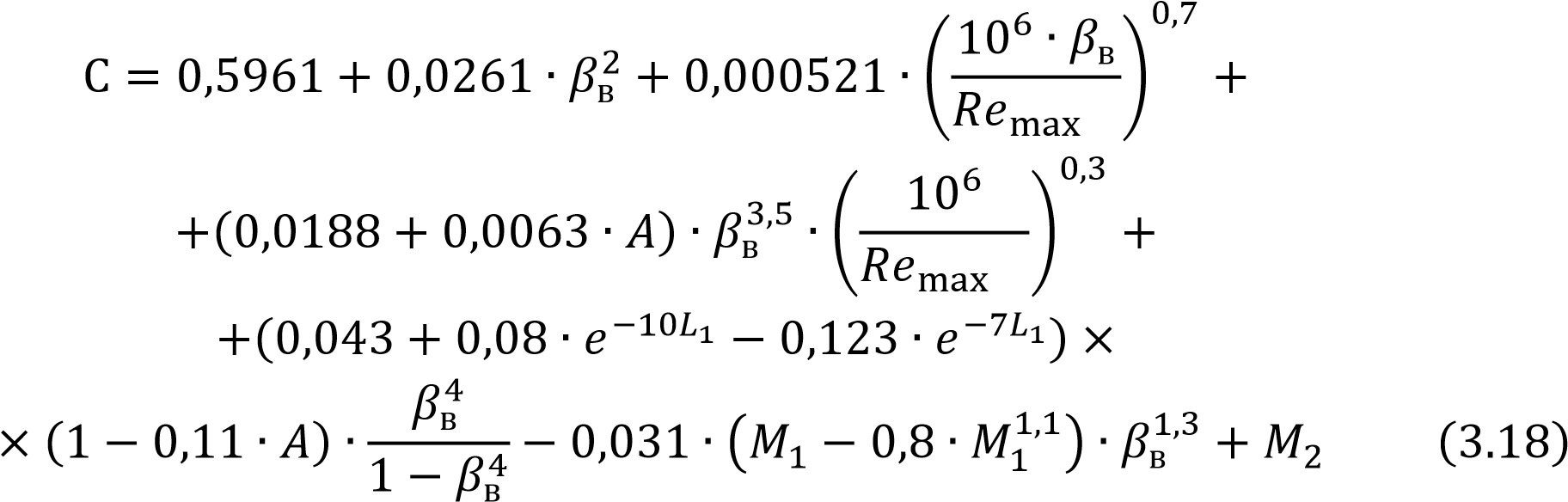 Коэффициент А для данного уравнения определяется следующим образом 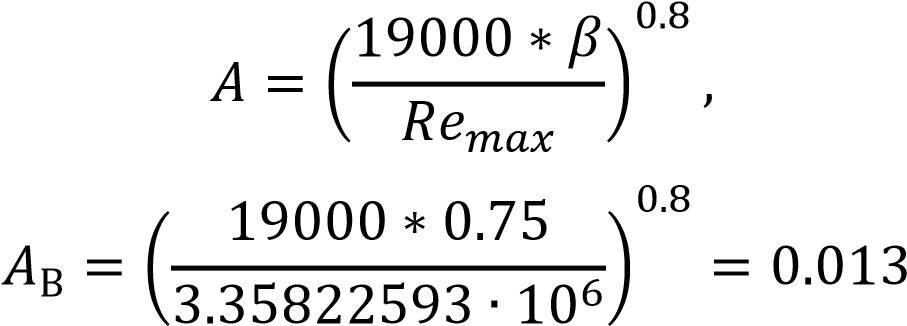 , , Значения 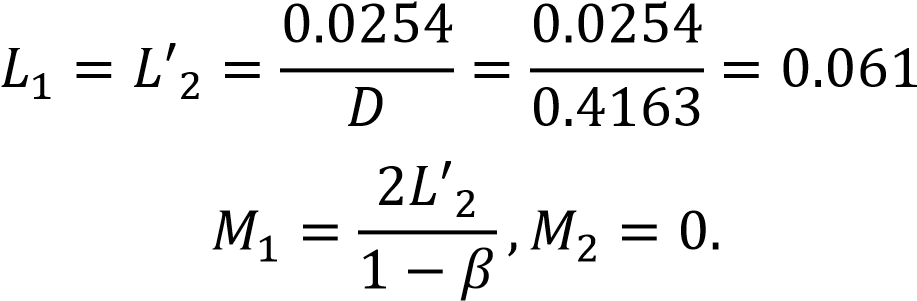 , , Подставляем полученные коэффициенты в формулу (3.19) и найдём коэффициенты истечения С1, С2 При использовании любого из трех способов отбора давления коэффициент расширения рассчитывают по формулам 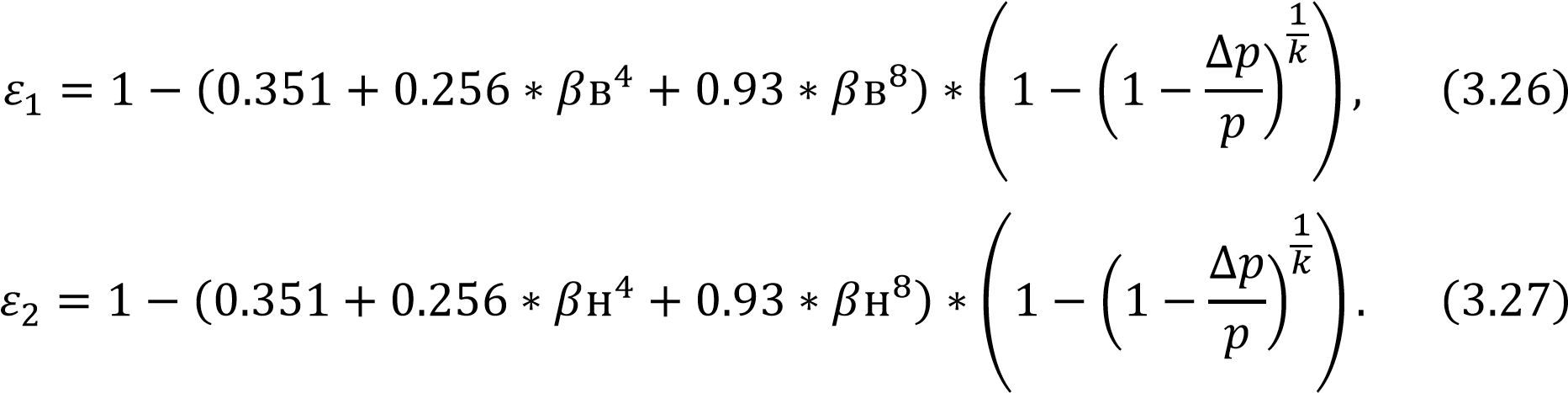 где Подставив численные значения получим Коэффициенты скорости Е1 и Е2 определяются уравнениями 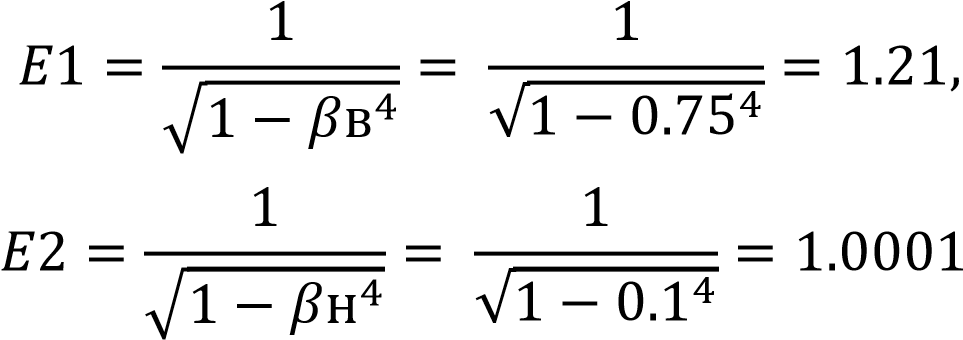 . . Шероховатость внутренней поверхности измерительного трубопровода примем удовлетворяющей требованиям пункта 7.1.5 – без дефектов и различных осадков в виде пыли, песка, металлической окалины и других загрязнений. Поэтому коэффициенты, учитывающие шероховатость внутренней поверхности измерительного трубопровода Аналогичным образом примем радиус входной кромки диафрагмы не превышающим 0.0004d т.к. диафрагма должна быть изготовлена в соответствии с требованием. В этом случае коэффициенты, учитывающие притупление входной кромки диафрагмы Подставив полученные значения в формулы (3.17 – 3.18) получим значения вспомогательных величин 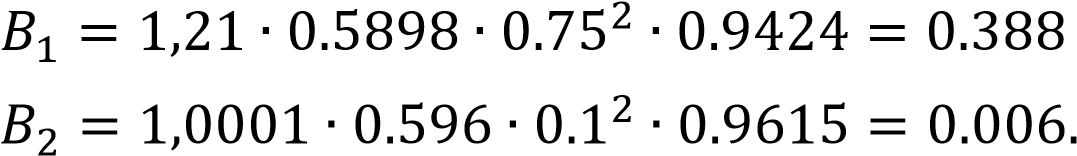 , , Рассчитываем значения вспомогательных величин δ1 и δ2 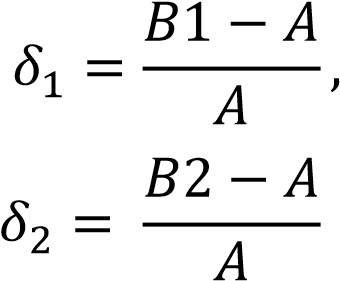 . . Подставив найденные значения из уравнений (3.15) и (3.32,3.33), получила  . . Так как величины Относительно неизвестной величины β решают следующее уравнение Для решения этого уравнения можно применить любой итерационный метод. Используя, метод бисекции провела следующие расчеты Рассчитывают значение β по формуле Для значения β рассчитывают значение вспомогательной величины B по формуле (3. Затем проверяют выполнение неравенства Если неравенство (3.40) не выполняется, то рассчитывают новое значение β по формуле (3. Выбор значений Итерацию производила в программе Matlab, количество шагов итерации составило 14 в результате которых получились значения Согласно ГОСТ 8.586.2 (пункт 5.3.1) значение числа Re должно быть более 5000 и (1.7·105· Используя значение где где 1/ ̊С. Расчёт коэффициента где Для 12Х18Н10Т: 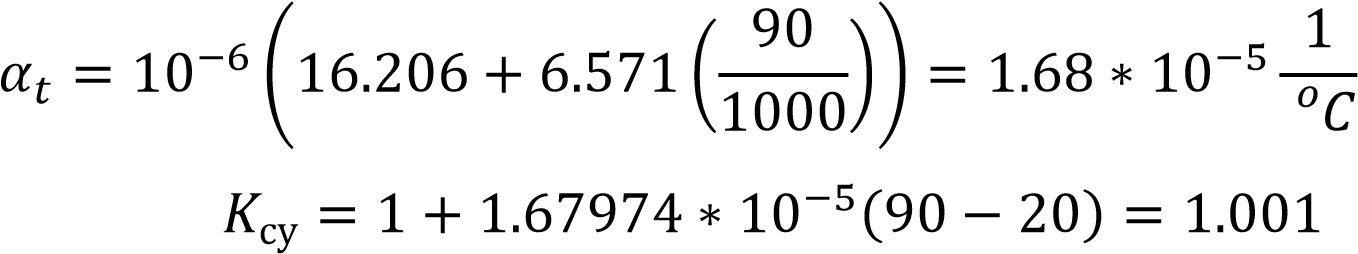 . . Подставив полученные значения в выражение (3.41), получила |
