Бакаленко. Разработка расходомера переменного перепада давлений и определение его метрологических характеристик

• Название: Разработка расходомера переменного перепада давлений и определение его метрологических характеристик
• Дата: 28.11.2022
• Размер: 1.89 Mb.
• Имя файла: Бакаленко.docx
• Тип: Реферат; #817139
• страница: 7 из 7

3.4 Требования к монтажу

Общие требования к установке СУ, приведенные в ГОСТ 8.586.1 (раздел 7) [1], применяют совместно с дополнительными специальными требованиями настоящего стандарта к диафрагмам.

Необходимую минимальную длину прямолинейных участков ИТ определяют в зависимости от вида МС, их размещения на ИТ и относительного диаметра отверстия диафрагмы.

Необходимая минимальная относительная длина прямолинейных участков ИТ между диафрагмой и МС

Длина прямолинейного участка до диафрагмы выбирается в зависимости от типа местного сопротивления для различных 𝛽. В нашем случае это конфузор.

Так как значение 𝛽 = 0.555 - промежуточное, не указанно в таблице 4, минимальную длину прямолинейных участков ИТ рассчитывают по формуле с применением линейной интерполяции данных таблицы

, (3.82)

где 𝛽₁, 𝐿₁ - ближайшее меньшее к величине 𝛽 значение относительного диаметра диафрагмы и соответствующее ему значение относительной длины прямолинейного участка ИТ, указанные в таблице 4;

𝛽₂, 𝐿₂ - ближайшее большее к величине 𝛽 значение относительного диаметра диафрагмы и соответствующее ему значение относительной длины прямолинейного участка ИТ, указанные в таблице 4.

Результат расчета по формуле (3.82) округляют до целого числа.

Таким образом, необходимая минимальная относительная длина прямолинейных участков ИТ между диафрагмой и МС равна 9*D = 3.74 м.

Диафрагма должна быть расположена в ИТ таким образом, чтобы было обеспечено течение среды от входного торца диафрагмы к выходному и должна быть расположена перпендикулярно к оси ИТ в пределах ± 1°. Диафрагма должна быть центрирована в трубопроводе.

4 Оценка погрешности расходомера

Для расчета неопределённости расхода среды, в качестве которой выступает жидкость, воспользуемся формулой из ГОСТ 8.586.5-2005 (пункт

10.2) [3]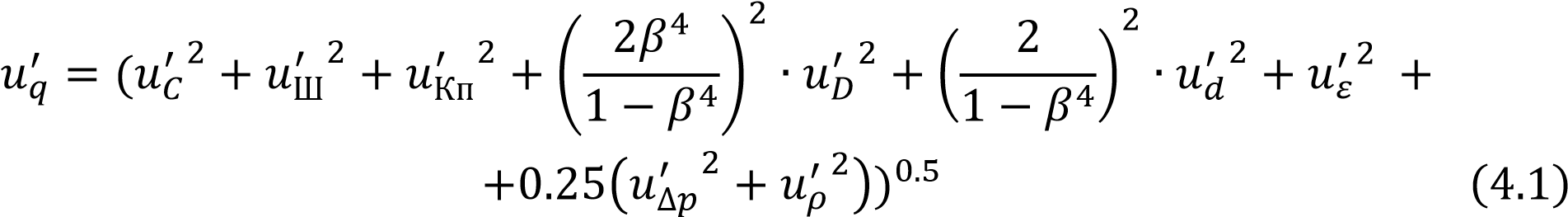



где – относительная стандартная неопределенность коэффициента истечения, %;

– относительная стандартная неопределенность поправочного

к оэффициента, учитывающего шероховатость внутренней поверхности измерительного трубопровода, %;

– относительная стандартная неопределённость поправочного

коэффициента, учитывающего притупление входной кромки диафрагмы, %;

𝛽 – относительный диаметр отверстия СУ;

𝑢_𝐷^′ – относительная стандартная неопределенность внутреннего диаметра ИТ, %;

𝑢_𝑑^′ – относительная стандартная неопределенность диаметра отверстия СУ при рабочей температуре среды, %;

𝑢_∆^′ _𝑝 – относительная стандартная неопределенность результата измерения перепада давления, %;

𝑢_𝜌^′ – относительная стандартная неопределенность результата плотности среды, %;

Относительную стандартную неопределенность коэффициента истечения с учетом влияющих факторов рассчитывают по формуле 10.17 пункта 10.3.1:

, (4.2)

где – неопределенность коэффициента истечений, определяемая согласно пункту 5.3.3.1 из ГОСТ 8.586.2-2005 [2] по формуле

, (4.3)

• 
  – составляющая неопределенности коэффициента истечения, которая
  

гильзой термометра, для упрощения расчетов примем длины прямолинейных участков, соответствующих пункту 6.3.6. Следовательно, 𝑈_𝐿^′ = 0.

– составляющая неопределенности коэффициента истечения, которая обусловлена сокращением длины прямолинейных участков между СУ и гильзой термометра, для упрощения расчетов примем длины прямолинейных участков, соответствующих пункту 6.3.6. Следовательно, .

– составляющая неопределённости коэффициента истечения, которая обусловлена сокращением оси диафрагмы относительно оси ИТ.

Для упрощения расчётов примем, что расстояние между осью отверстия диафрагмы и ИТ в перпендикулярном и параллельном направлении к оси отверстия для отбора давления удовлетворяет условиям, изложенным в пункте 6.5.3. Следовательно, .

𝑈_ℎ^′ – составляющая неопределённости коэффициента истечения, которая обусловлена разностью значения диаметра между смежными секциями ИТ, примем её удовлетворяющей условиям пункта 6.4.4 [2]. Следовательно, 𝑈_ℎ^′ =

0.

Используя формулу (4.2) и подставляя полученные значения, неопределенность коэффициента истечения будет равной:



Согласно пункту 10.3.2 [3], значения относительной стандартной неопределённости внутреннего диаметра ИТ и относительной стандартной неопределённости диаметра отверстия СУ при рабочей температуре среды принимаются равными:

𝑢_𝐷^′ = 0,1%.

𝑢_𝑑^′ = 0,02%. Относительная стандартная неопределённость коэффициента расширения рассчитывают по формуле (10.3.3) [3]: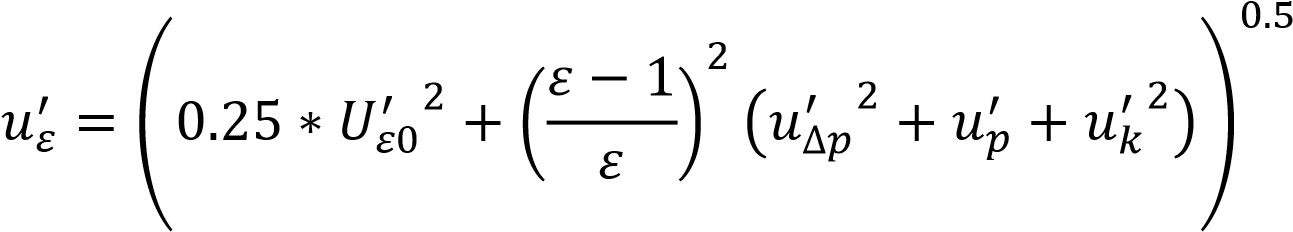

, (4.5)

где - неопределенность коэффициента расширения, рассчитывается по формуле:

. (4.6)

Относительная стандартная неопределённость результата измерения перепада давления при допущении линейной функции преобразования для дифференциального манометра класса точности 0,075, находится по следующей формуле:



где – относительная погрешность дифференциального манометра;

– верхний предел измерений выбранного дифференциального манометра;

– измеряемое значение перепада давления.

Относительная стандартная неопределенность результата плотности среды находим согласно формуле 10.29 [3]:

,

где – неопределённость приписываемая уравнению, применяемому для расчёта плотности (значение приводят в соответствующих документа, устанавливающих методы косвенного расчета плотности), 0,01%; и - коэффициенты чувствительности для давления и температуры.

и - относительная стандартная неопределённость измерения

температуры и давления.

Коэффициенты влияния температуры на плотность определены с использованием метода конечных разностей (п. 10.12 [3]):

,

где – изменение определяемой величины у при изменении yi на величину

, в соответствии с формулой (4.8) изменение плотности с 90 ^oC на 100 ^oC.

При температуре 90 ^oC плотность составляет 5.6663 кг/м3, а при 100 ^oC,

5. кг/м3. Таким образом = 0.151 y – определяемая величина, в данном случае плотность при рабочей

температуре t = 90 ^oC; yi - измерение i-й величины, т.е температуры t = 90 ^oC;

Т.к класс точности термометра задан абсолютной погрешностью, то неопределенность результата измерения температуры рассчитывается по формуле

,

где – основная абсолютная погрешность термометра, y – рабочая температура по заданию, y = 90 .

Относительная стандартная неопределенность измерения давления находится из класса точности манометра для измерения абсолютного давления, в моем случае класс точности манометра 1.5 находится по формуле , (4.11)

где 𝛿 – относительная погрешность манометра;

𝛾_в– верхний предел измерений выбранного манометра; 𝛾 – измеряемое значение давления.

Коэффициенты влияния давления на плотность определены с использованием метода конечных разностей

, (4.12)

где ∆𝑦 – изменение определяемой величины у при изменении yi на величину ∆𝑦𝑖, в соответствии с формулой (4.8) изменение плотности с 0.5 МПа на 0.501 МПа. При избыточном давлении 0.5 МПа плотность составляет 5.6663 кг/м3, а при давлении 0.501 МПа, ρ = 5.677 кг/м3. Таким образом ∆𝑦 = 0.0107; y – определяемая величина, в данном случае плотность 𝜌 при рабочем

давлении 0.5 МПа; yi - измерение i-й величины, т.е давления 0.5 МПа.

Подставляя значения в формулу (4.5), и принимая 𝑢_𝑘^′ = 0.01%, получила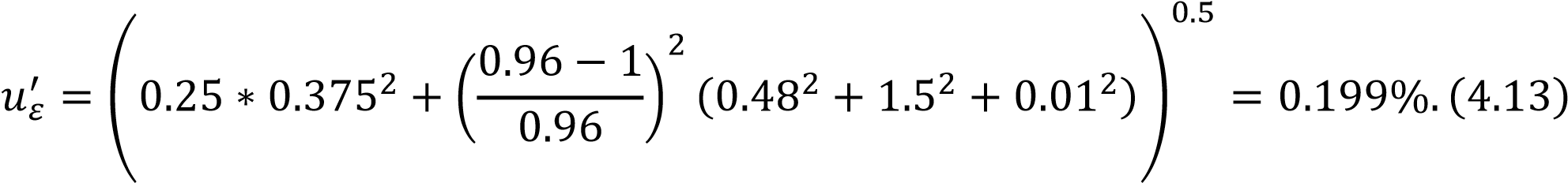



Относительная стандартная неопределённость поправочного коэффициента, учитывающего шероховатость внутренней поверхности измерительного трубопровода принимается равной нулю, так как шероховатость внутренней поверхности измерительного трубопровода примем удовлетворяющей требованиям пункта 7.1.5 - без дефектов и различных осадков в виде пыли, песка, металлической окалины и других загрязнений.

Следовательно, .

После нахождения всех составляющих, рассчитывают стандартную неопределённость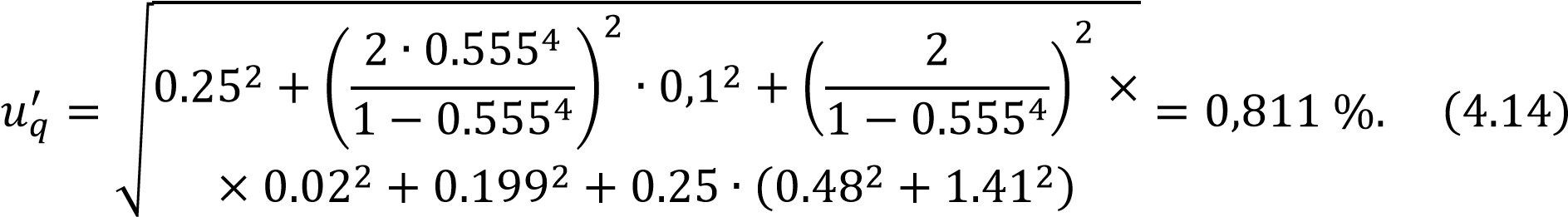



Расширенная неопределённость расхода получается путём умножения стандартной неопределённости на коэффициент охвата 𝑘 = 2, что соответствует уровню доверия, равному приблизительно 95 % (пункт 10.1.3). Расчётная формула:

. (4.15)

Подставив значения в формулу (4.15) получила

. (4.16)

Заключение

В курсовом проекте разработан расходомер переменного перепада давлений с диафрагмой, которая выступает в качестве сужающего устройства. Был описан метод переменного перепада давлений.

Было разработано сужающее устройство, осуществлен выбор дополнительных средств измерений таких как дифманометр, манометр, термометр, и были определены и характеристики.

В итоге работы получила расширенную неопределённость расхода равную 1,622%, поэтому можно считать что данная система обеспечивает качественное измерение расхода.



Список литературы 1. Измерение расхода и количества жидкостей и газов с помощью стандартных сужающих устройств. межгосударственных стандартов. Часть 1. Принцип метода измерений и общие требования: ГОСТ 8.586.12005. - Введ. 01.01.07. - Межгосударственный совет по стандартизации, метрологии и сертификации, 2005.

2. 
   Измерение расхода и количества жидкостей и газов с помощью стандартных сужающих устройств. межгосударственных стандартов. Часть 2. Диафрагмы. Технические требования: ГОСТ 8.586.2-2005. - Введ. 01.01.07. - Межгосударственный совет по стандартизации, метрологии и сертификации, 2005.
   
3. 
   Измерение расхода и количества жидкостей и газов с помощью стандартных сужающих устройств. межгосударственных стандартов. Часть 5. Методика выполнения измерений: ГОСТ 8.586.5-2005. - Введ. 01.01.07. - Межгосударственный совет по стандартизации, метрологии и сертификации, 2005.
   
4. 
   Нормируемые метрологические характеристики средств измерений: ГОСТ 8.009-84. - Введ.01.01.86 – Государственный комитет СССР по стандартам, 1985.
   
5. 
   Михайлов В. Б., Бакаленко В. И., Метрология, методы и приборы технических измерений: курс лекций / Минск, 2013г. – 252 с.
   
6. 
   Неопределенность измерения. Руководство по выражению неопределенности измерения: ГОСТ 34100.3-2017. – Введ. 01.09.18. -
   

Межгосударственный совет по стандартизации, метрологии и сертификации, 2017.

2. 
   Гири классов Е₁, Е₂, F₁, F₂, М₁, М_1-2, М₂, М_2-3 и М₃. Часть 1. Метрологические и технические требования: ГОСТ OIML R 111-1-2009 Введ. 01.07.12. - Межгосударственный совет по стандартизации, метрологии и сертификации, 2009.
   
3. 
   Газ природный. Методы расчета физических свойств. Определение физических свойств природного газа, его компонентов и продуктов его переработки: ГОСТ 30319.1-96. - Введ. 01.07.97. - Межгосударственный совет по стандартизации, метрологии и сертификации, 1996.