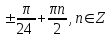Итоговая работа. Итоговая дистанционная работа Кирсанов А.А.. Разработка урока математики в 11 классе по теме Применение производной к исследованию функции
 Скачать 1.72 Mb.
|
|
Разработка урока математики в 11 классе по теме «Применение производной к исследованию функции», подготовлена учителем математики МБОУ Новомихайловской СОШ Кирсановым Анатолием Анатольевичем Тип урока: обобщения и систематизации знаний. Цели урока: 1) обобщить и систематизировать знания обучающихся по теме «Применение производной к исследованию функции»; повторить таблицу производных, правила дифференцирования, физический и геометрический смыслы производной, признаки возрастания и убывания функции, критические и стационарные точки, экстремумы функции; закрепить навыки техники дифференцирования, умения применять производную к исследованию функции и построению графиков; создать дифференцированные условия контроля (самоконтроля, взаимоконтроля) усвоения знаний и умений; выработать специфические умения и навыки по работе с графиком производной функции для их применения при сдаче ЕГЭ – 2022; 2) содействовать развитию мыслительной деятельности при выполнении группового задания, творческих способностей, логического мышления учащихся; продолжить развитие умений видеть целое, выделять главное и части его составляющие; навыков систематизировать и обобщать знания; продолжать развитие математической речи, графической культуры обучающихся; 3) продолжить воспитание активности, культуры общения, взаимопомощи, ответственности, самоконтроля; содействовать пониманию, что воображение и мышление – необходимые атрибуты математики; воспитывать уверенность в своих силах, умение отстаивать свою точку зрения путем создания провокационных ситуаций на уроке. Планируемые результаты: Предметные: закрепление изученного материала по теме «Применение производной к исследованию функции», осознание значения данной темы для подготовки к ЕГЭ – 2022, способствование совершенствованию практических навыков решения заданий из открытого банка (ОБЗ – 11 – 2022, базовый и профильный уровни) на применение свойств производной, работе с графиками производных. Метапредметные: способность принимать и сохранять цели и задачи учебной деятельности, находить средства и способы её осуществления; умения контролировать и оценивать учебные действия, определять наиболее эффективные способы достижения результата; готовность слушать собеседника и вести диалог; излагать своё мнение и аргументировать свою точку зрения; умение самостоятельно осуществлять поиск в различных источниках, отбор, анализ, систематизацию и классификацию информации, представлять ее в понятной форме; умение использовать математические средства наглядности (графики, таблицы и др.) для иллюстрации, аргументации; умение договариваться о распределении функций и ролей в совместной деятельности, осуществлять взаимный контроль, адекватно оценивать собственное поведение и поведение окружающих. Личностные: умение вести диалог; воля, инициатива и настойчивость в достижении цели; независимость и критичность мышления; навыки сотрудничества, умение взаимодействовать с одноклассниками и взрослыми; самостоятельность и ответственное отношение к обучению, способность и готовность к саморазвитию и самообразованию на протяжении всей жизни; сознательное отношение к непрерывному образованию как к условию успешной профессиональной и общественной деятельности; рефлексия собственной деятельности. Формы организации учебной деятельности: фронтальная, групповая, индивидуальная, коллективная. Технологии, используемые на учебном занятии: информационные технологии, технология сотрудничества, технология дифференцированного обучения и индивидуального подхода. Ход урока. I. Мотивационно-целевой этап. Учитель: Здравствуйте, ребята! В этом учебном году у нас более 100 уроков алгебры. И на каждом уроке вы узнаете что-то новое, интересное и полезное! Сегодняшний урок не исключение, так как мы продолжаем готовиться к ГИА. Нас ждут не только задания школьного курса, но и специфические упражнения, так как многие из вас выбрали профильный экзамен. Чтобы их решить вам пришлось проявить терпение, настойчивость и смекалку. Учитель: А начать наш урок обобщения и систематизации знаний по теме «Применение производной к исследованию функции» я хотел бы с одного замечательного высказывания Алексея Николаевича Крылова, математика и кораблестроителя, жившего в 19 веке. Кто зачитает его вслух? "Рано или поздно всякая правильная математическая идея находит применение в том или ином деле". А сейчас давайте повторим теоретический материал, который будем использовать сегодня на уроке. Наша «Утренняя мантра» Учащиеся: Фронтальный опрос. Операция нахождения производных – это дифференцирование. Определение производной. Производная константы? 0 Переменной? 1 Производная суммы равна сумме производных Производная разности равна разности производных Производная произведения, частного. Производные тригонометрических функций. Производная сложной функции равна произведению производной внутренней функции и производной внешней функции. Физический смысл производной: производная – это мгновенная скорость. Геометрический смысл произвольной: производная функции в точке – это угловой коэффициент касательной в данной точке и тангенс угла наклона касательной в данной точке к оси х. Если касательная в точке горизонтальная, то производная функции в этой точке равна 0. Если производная > 0 на промежутке, то функция возрастает на этом промежутке. Если производная < 0 на промежутке, то функция убывает на этом промежутке. Критические точки – это внутренние точки области определения функций, в которых производная равна 0 или не существует. Стационарные точки – это внутренние точки области определения функций, в которых производная равна 0. Точки экстремума функции – это точки максимума и минимума. Если в точке производная меняет знак с + на - , то данная точка является точкой максимума. Если в точке производная меняет знак с - на + , то данная точка является точкой минимума. Схема исследования функции. Асимптоты. Учитель: А сейчас с помощью игры «Домино» проверим вашу технику дифференцирования, так как без этого работа с производной не имеет смысла. Ребята! У вас на партах лежат карточки с многочленами. Ученик у доски показывает карточку, которую будем считать первой «фишкой» домино. Тот, у кого на парте производная данного многочлена, быстро идет к доске и «прикладывает» свою «фишку» к предыдущей. Следующий ищет производную второй «фишки» и т.д. Цель - выстроить цепочку из «фишек» таким образом, чтобы они соприкасались друг с другом. Учащиеся:
Молодцы! II. Практико-ориентированный этап. Учитель: Ребята! Урок обобщения и систематизации знаний предполагает, что вы демонстрируете свои знания по изученной теме. Вы получили домашнее задание по группам. Я тоже дома выполнил эти задания. Для наглядности они будут на слайдах, которые вы, естественно, не видели. Итак, ребята представляют свою работу по группам, а мы с помощью слайдов проверяем. Отметки кураторы оставляют у меня на столе. Но сначала давайте повторим схему исследования функции. Внимание на слайд! Вы согласны? (провокационная ситуация, так как в схеме нарушена последовательность). (СЛАЙД 2). Схема исследования функции 1. Дополнительные точки (при необходимости). 2. Промежутки возрастания и убывания функции. 3. Найти область определения функции. 4. Производная и критические точки. 5. Определить четность или нечетность, периодичность. 6. Построение графика на основании проведенного исследования. 7. Значение функции в критических точках. 8. Точки пересечения графика с осями координат. 9. Точки экстремума. Учащиеся: (СЛАЙД 3). Теперь схема верная?! Схема исследования функции Найти область определения функции. Определить четность или нечетность, периодичность. Точки пересечения графика с осями координат. Производная и критические точки. Промежутки возрастания и убывания функции. Точки экстремума. Значение функции в критических точках. Дополнительные точки (при необходимости). Построение графика на основании проведенного исследования. Учитель: Приглашаю для защиты первую группу со своим куратором. Прошу к проектору. Учащиеся: 1 группа. Исследовать и построить график функции, содержащей точку перегиба: у=5х3-3х5 (СЛАЙД 4,5,6).   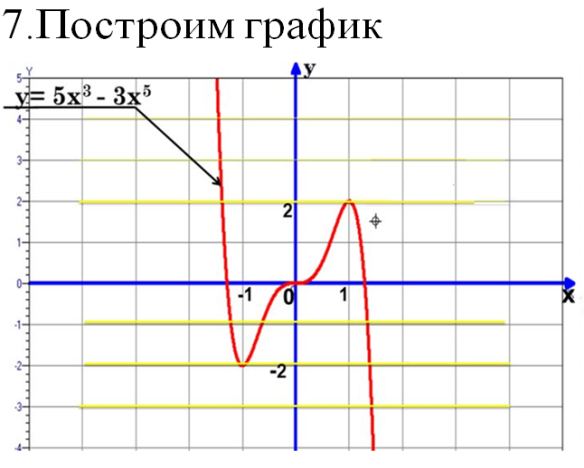 Учащиеся: 2 группа. Исследовать и построить график функции, содержащей вертикальную и наклонную асимптоты (СЛАЙД 7,8,9,10,11).  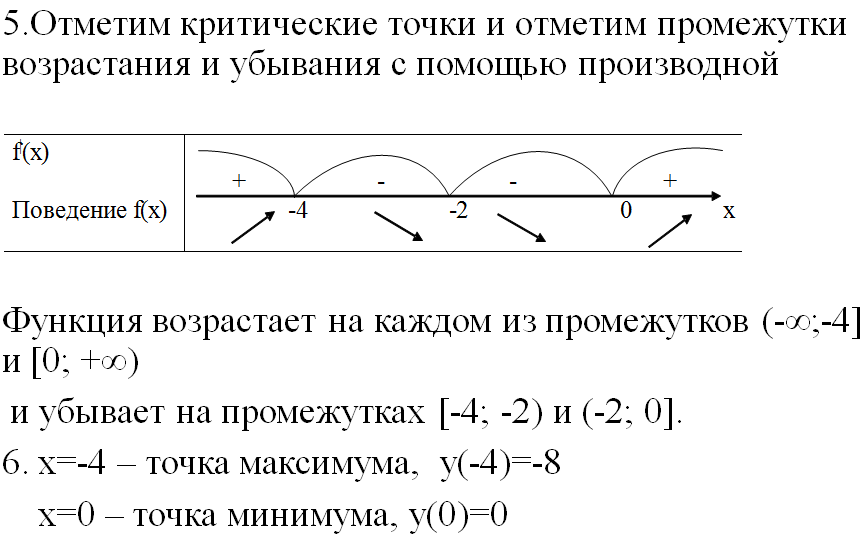   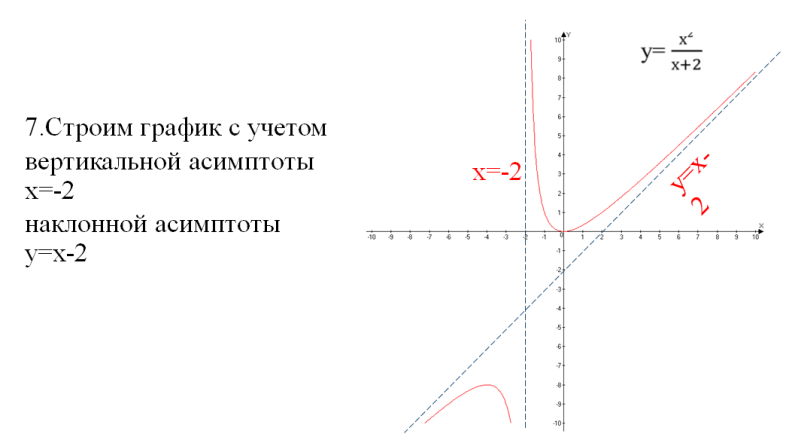 III. Контрольно-оценочный этап. Учащиеся: Решение ОБЗ – 11-2022, базовый уровень, задание 14: №1,3,9.; профильный уровень, задание 7: №2,4,7(СЛАЙДЫ 12-15). 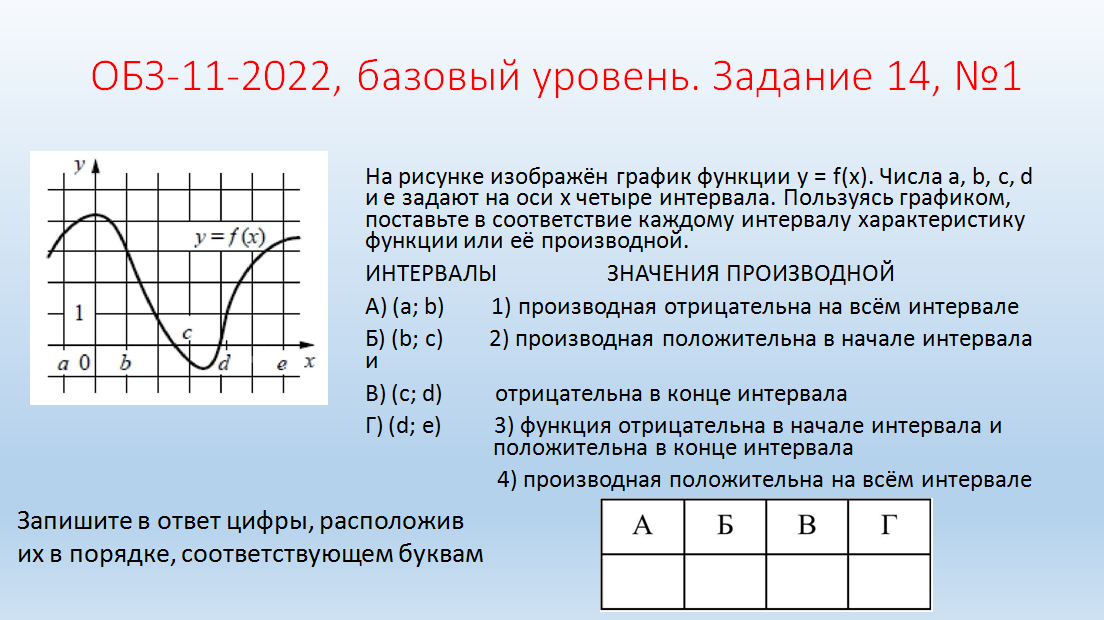  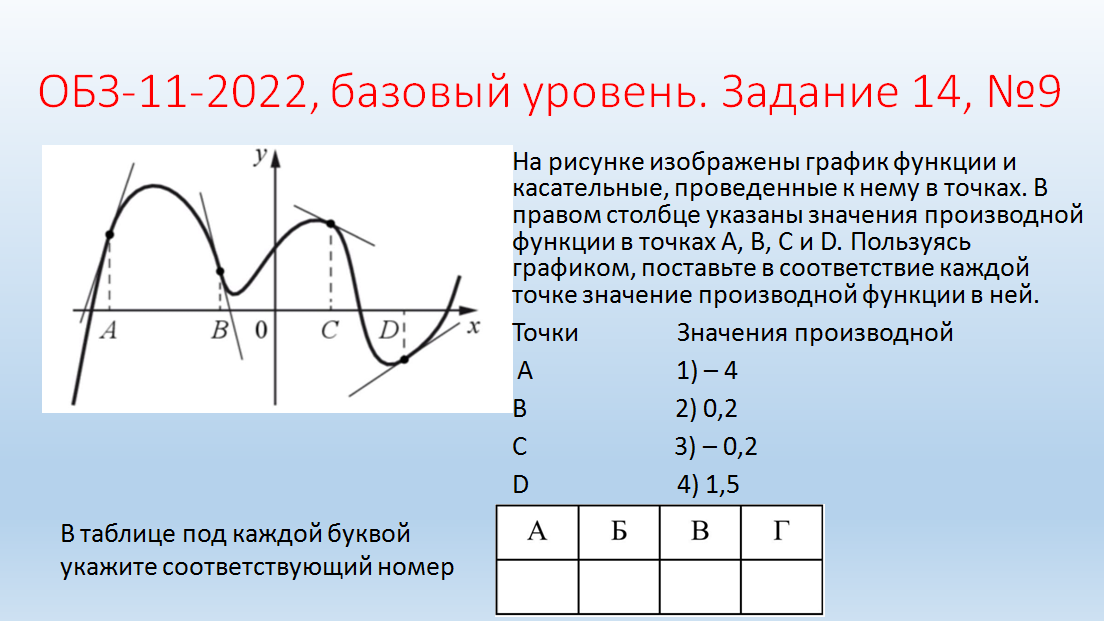 (СЛАЙД 16). Ответы. Задание 14. №1: А-2, Б-1, В-3, Г-4; №3: А-1, Б-4, В-3, Г-2; №9: А-4, Б-1, В-3, Г-2. Учащиеся: Задание 7. №2: 6; №4: 0,25; №7: 5. Решение ОБЗ – 11-2022, профильный уровень, задание 7: №8,9,10,11,14,15 (СЛАЙДЫ 17-25). 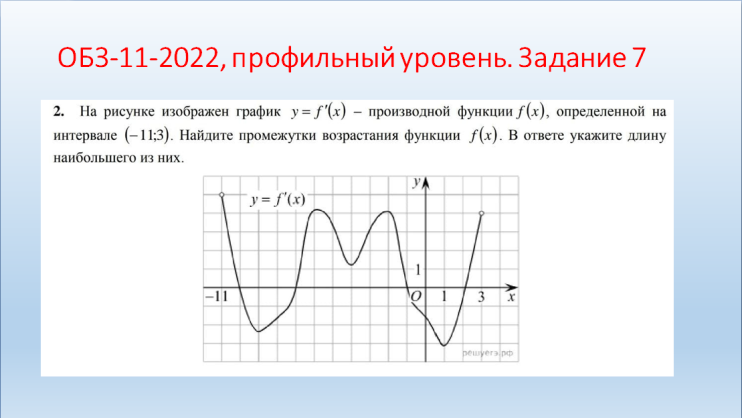 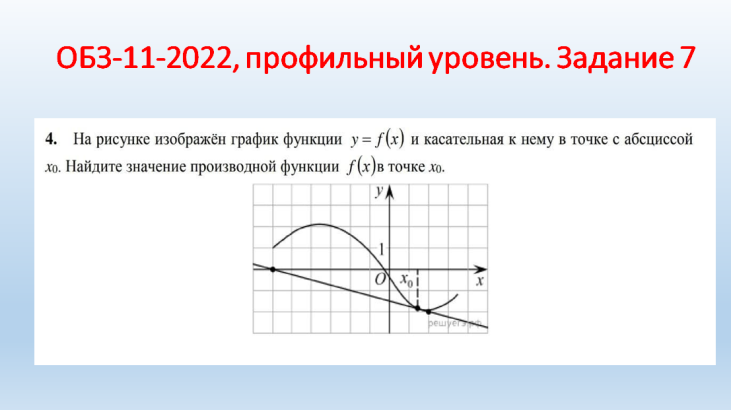  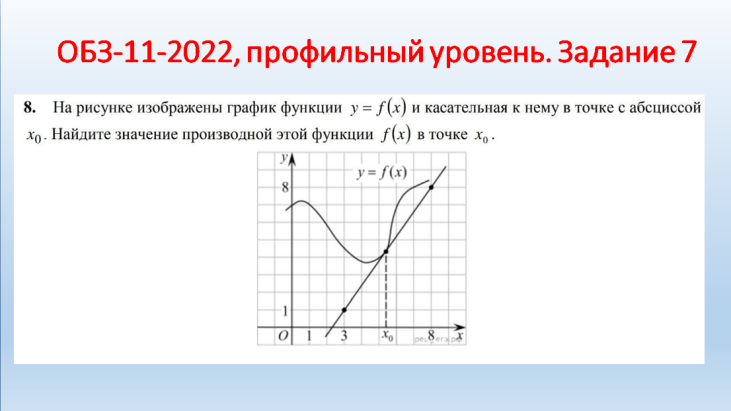 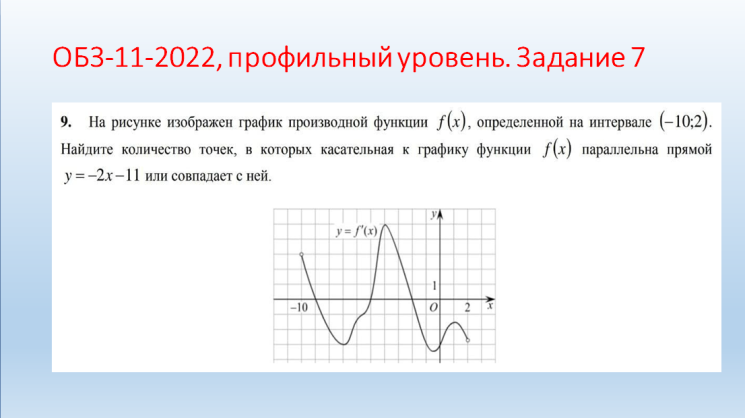 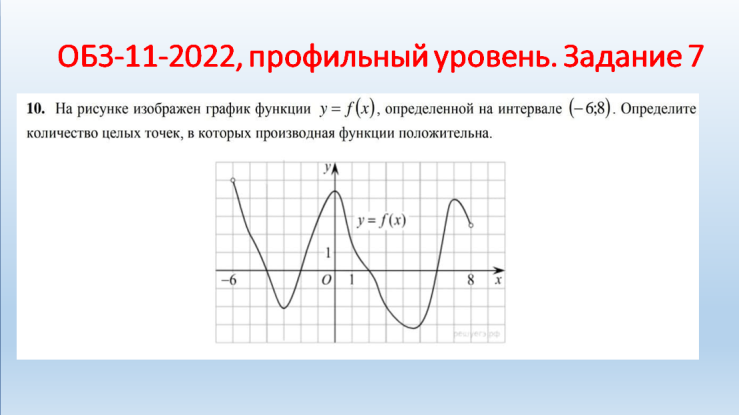 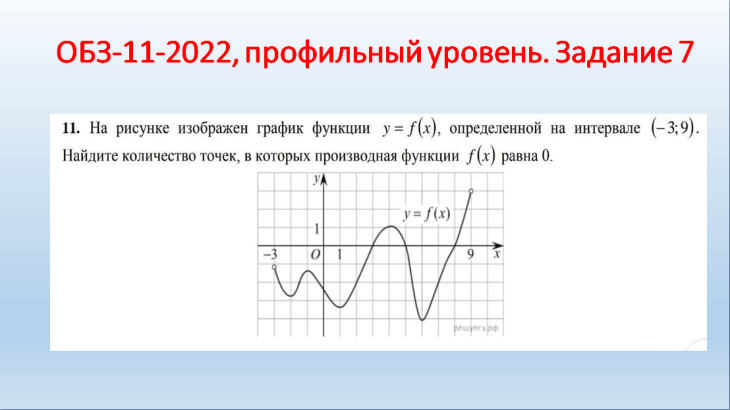 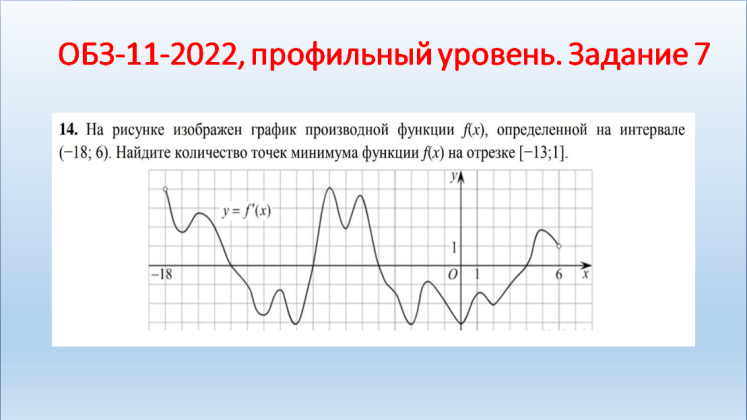 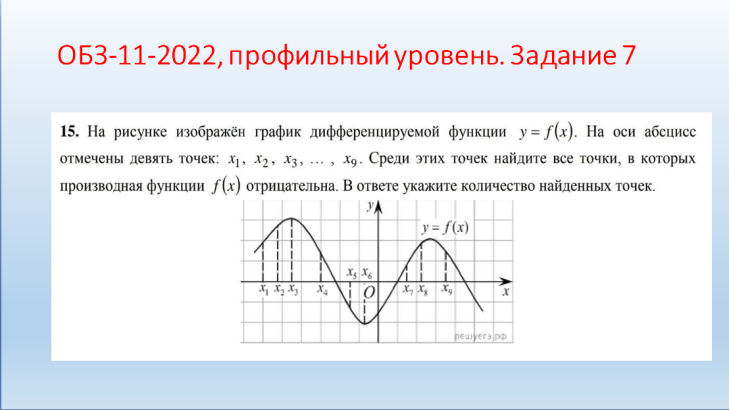 (СЛАЙД 26). Ответы. Задание 7. №8: 1,4; №9: 5; №10: 4; №11: 5; №14: 1; №15: 3. Учитель: Задание на дом. Учебник, №930 (1,3), №933* (2) IV. Рефлексивно-обобщающий этап. Учитель: В завершении урока давайте вместе закончим фразы, предложенные на слайде. (СЛАЙД 27). Если ваш ответ положительный, то поднимаем большие пальцы обеих рук вверх, а если отрицательный – вниз. Учитель: Учащиеся: Рефлексия: На уроке я работал активно/ пассивно Своей работой на уроке я доволен/ не доволен Урок для меня показался коротким/длинным Моё настроение стало лучше/ хуже Материал урока мне был полезен/ бесполезен интересен/ скучен Всем спасибо за урок! |
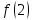, если 
; 
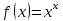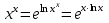
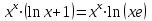
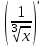
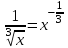
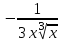
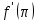, если 
.
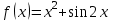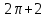
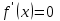, если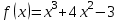 
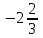; 0.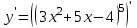
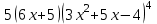
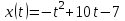. Найдите скорость при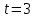 
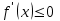, если 
.
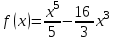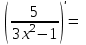
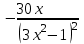
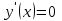, если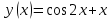 
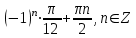
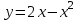в точке с абсциссой 
.
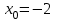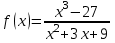в точке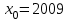 
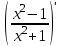
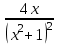
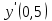, если 
.
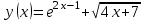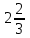
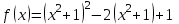в точке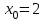 
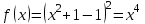
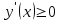, если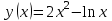 
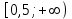
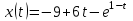, где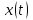 
- координата точки в момент времени 
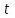. Найдите время, в момент которого скорость равнялась 7.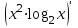
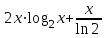
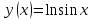
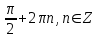
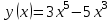
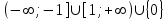
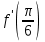, если 
.
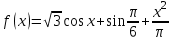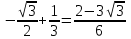
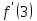, если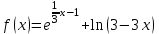 
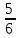
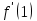, если 
. 
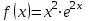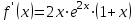
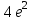
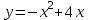в точке с абсциссой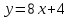 
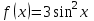. Вычислить 
. 
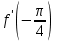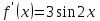
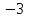
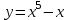в начале координат? В ответе укажите градусную меру этого угла.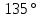
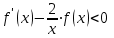, если 
.
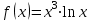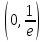
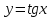
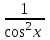
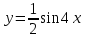. Укажите абсциссы точек, в которых касательная к графику данной функции составляет с осью 
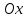угол 
