Тригонометрические функции. Разработка урока Обратные тригонометрические функции и их вычисления
 Скачать 0.69 Mb. Скачать 0.69 Mb.
|
|
Основные тригонометрические тождества Тригонометрические функции связаны между собой следующими основными тождествами:
Из тождества I вытекают формулы С помощью основных тригонометрических тождеств решается задача отыскания значений всех тригонометрических функций по известному значению одной из них. Формулы сложения аргументов 1. 2. 3. 4. 5. 6. Формулы двойных и половинных углов Полагая 1. 2. 3. Из формулы 2 вытекают два часто употребляемых соотношения 4. 5. Из формул 4. и 5. можно получить формулы половинных углов: 6. где знак зависит от четверти, в которой оканчивается угол /2. Заменяя в равенствах 1.- 3. 2 на , а на /2, находим: 7. 8. 9.  Кроме того, и выражаются через тангенс половинного угла по формулам 10. 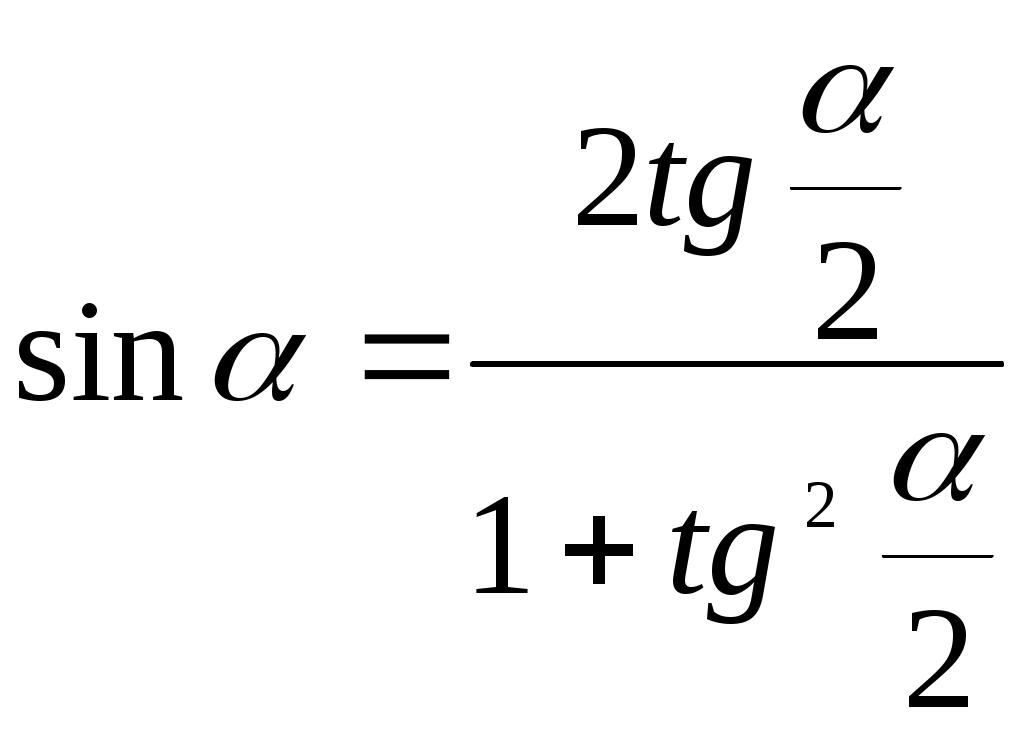 11.  Формулы приведения Значения тригонометрических функций острых углов вычисляют по таблицам. Значения функций любых углов можно вычислить с помощью формул приведения к острому углу. Сформулируем общее правило написания формул приведения: Знак тригонометрической функции определяют по первоначально заданному углу. Если аргумент можно представить как сумму или разность , 2 и острого угла, то название функции не изменяют. Если аргумент можно представить как сумму или разность /2, 3/2 и острого угла, то название функции изменяют на сходное (синус – на косинус, тангенс – на котангенс).
Формулы сложения одноименных функций Формулы сложения одноименных тригонометрических функций позволяют преобразовать сумму и разность функций в произведение этих функций. Они имеют следующий вид: 1. 2. 3. 4. Как их получаем? Сложим соответственно левые и правые части формул сложения аргументов 1. и 2., введем новые переменные: Т.е. Теперь заменим Аналогичные действия производим с формулами суммы и разности аргументов косинусов. Свойства и графики тригонометрических функций Область определения – множество всех действительных чисел. Область изменения (множество значений) – промежуток Функция Функция Нули функции: Промежутки знакопостоянства: Функция возрастает при и убывает при Функция минимальные значения, равные -1, при и максимальные значения, равные 1, при 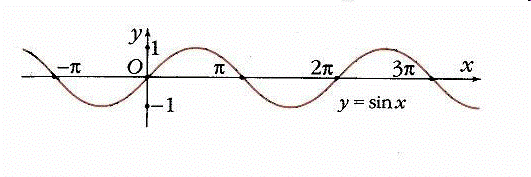 График функции Область определения – множество всех действительных чисел. Область изменения (множество значений) – промежуток Функция Функция Нули функции: Промежутки знакопостоянства: Функция возрастает при и убывает при Функция минимальные значения, равные -1, при и максимальные значения, равные 1, при 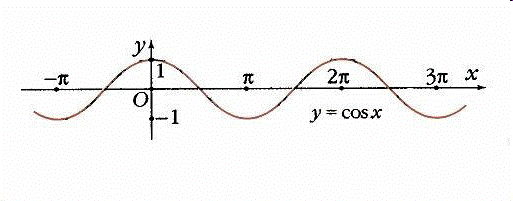 График функции Область определения – множество всех действительных чисел, кроме чисел Область изменения (множество значений) – множество всех действительных чисел. Функция Функция Нули функции: Промежутки знакопостоянства: Функция  График функции Область определения – множество всех действительных чисел, кроме чисел Область изменения (множество значений) – множество всех действительных чисел. Функция Функция Нули функции: Промежутки знакопостоянства: Функция  Обратные тригонометрические функции Теорема о корне П  усть функция усть функция у y=f(x) a 0 bx Доказательство: Докажем единственность корня уравнения Пусть существует с – еще один корень уравнения Т.е. Т.к. Следовательно, b - единственный корень.  y y y=f(x) a 0 bcx Функция Арксинусом числа a называется число из отрезка | |||||||||||||||||||||||||||||||
