Реферат 2 Введение 3 Формулировка основных моментов технических требований на проектируемый полувагон 5
 Скачать 0.96 Mb. Скачать 0.96 Mb.
|
7. Проектирование гасителя колебаний исходя из требуемого значения коэффициента относительного тренияДля центрального рессорного подвешивания будем проектировать гаситель колебаний аналогичный гасителю тележки модели 12-196-01. Проектируемую тележку будут подкатывать под вагон (модель 12-196-01) грузоподъемностью (Р) 69,5 тс (695 кН), тарой 24.5 тс (245 кН). Двухосная тележка модели 12-196-01имеет одинарное рессорное подвешивание, состоящее из семи двухрядных пружин. Жесткость одной пружины равна С = 44,845 тс/м. Из условия обеспечения нормируемых показателей динамических качеств проектируемой тележки потребная величина коэффициента относительного трения () должна быть в пределах 0,08 – 0,1, при прогибе рессорного подвешивания (fСТ) 68 мм. Принимаем, что фрикционные клинья зготовлены из материала чугун ВЧ 120, фрикционная планка – Сталь 30ХГСА, а надрессорная балка из стали марки 20ГЛ. Коэффициент трения между фрикционной планкой и клином принимаем равным 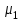 =0,15, а между клином и надрессорной балкой =0,15, а между клином и надрессорной балкой 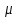 =0,1. Угол наклона рабочей поверхности клина и надрессорной балки принимаем равным =0,1. Угол наклона рабочей поверхности клина и надрессорной балки принимаем равным 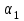 =45, а поверхности клина и фрикционной планки равным =45, а поверхности клина и фрикционной планки равным 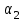 =2. =2.В таком случае прогиб подклиновой пружины будет равен: 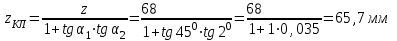 где z – прогиб рессорного подвешивания (fСТ). Нисходящее движение деталей гасителя колебаний Рассмотрим равновесие клина в момент времени t (рисунок 9, а). На рабочих поверхностях фрикционного клина возникают силы трения FН и F1Н. 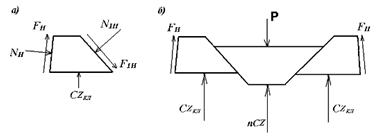 Рисунок 9 – Равновесие деталей гасителя колебаний при нисходящем движении Записав условия равновесия клина (сумма проекций всех сил на оси X и Y) и выполнив ряд преобразований, получим: 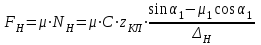 (7.1) (7.1)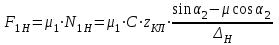 (7.2) (7.2)Где 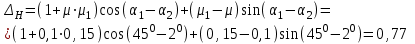 Вычислим силы трения на рабочих поверхностях: 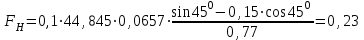 тс, тс,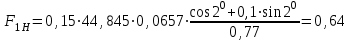 тс. тс.Суммарные силы трения, создаваемые гасителем колебаний при нисходящем движении будут равны: 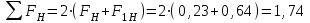 тс. тс.Вычислим реакцию рессорного подвешивания на действие внешней нагрузки Р при движении вниз : 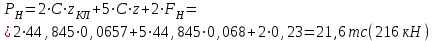 Коэффициент относительного трения: 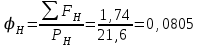 . .Восходящее движение деталей гасителя колебаний. Рассмотрим равновесие клина в момент времени t. На рабочих поверхностях фрикционного клина возникают силы трения FВ и F1В. 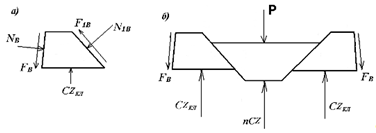 Рисунок 10 – Равновесие деталей гасителя колебаний при восходящем движении 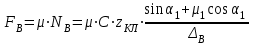 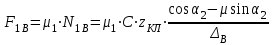 Где 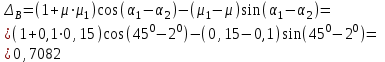 Вычислим силы трения на рабочих поверхностях: 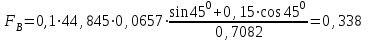 тс, тс,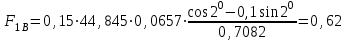 тс. тс.Суммарные силы трения, создаваемые гасителем колебаний при восходящем движении будут равны: 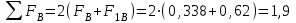 тс. тс.Вычислим реакцию рессорного подвешивания на действие внешней нагрузки Р при движении вверх (рисунок 17, б): 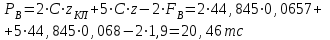 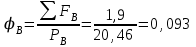 . .Среднее значение коэффициента относительного трения гасителя колебаний будет равно 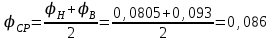 . .Спроектированный фрикционный гаситель колебаний с фрикционными клиньями из чугуна имеет коэффициент относительного трения равный потребному. 8. Расчет на прочность рамы полувагона на действие ударных продольных нагрузок I режимаСогласно требованиям норм должно обеспечиваться устойчивое движение колес по рельсовому пути. Однако при неблагоприятных условиях, когда горизонтальная сила динамического давления колеса на головку рельса 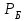 велика, а вертикальная велика, а вертикальная 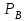 мала, то гребень колеса не будет скользить по головке рельса. мала, то гребень колеса не будет скользить по головке рельса.Поэтому для предупреждения сходов вагона в эксплуатации производится проверка устойчивости движения колеса по рельсу. Коэффициент запаса устойчивости рассчитывается по формуле: 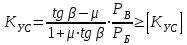 (8.1) (8.1)где – угол наклона образующей конусообразной поверхности гребня колеса с горизонталью (600); – коэффициент трения поверхностей колес и рельсов (0,25); РВ – вертикальная нагрузка от набегающего колеса на рельс; РБ – боковое усилие взаимодействия гребня набегающего колеса и головки рельса; 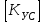 – допускаемое значение коэффициента запаса устойчивости (1,4). – допускаемое значение коэффициента запаса устойчивости (1,4).Вертикальная нагрузка от набегающего колеса на рельс вычисляется по формуле: 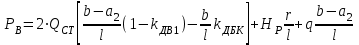 (8.2) (8.2)где 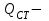 сила тяжести обрессоренных частей вагона, действующая на шейку оси колесной пары; сила тяжести обрессоренных частей вагона, действующая на шейку оси колесной пары;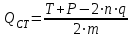 (8.3) (8.3)где Т и Р – тара и грузоподъемность вагона (24,5 и 69,5); q –сила тяжести необрессоренных частей, приходящихся на колесную пару 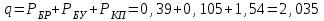 тс; тс;п – число осей в тележке (2); т – число шеек осей в тележке (4). 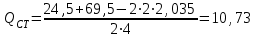 тс тсkДВ1 – расчетное значение коэффициента вертикальной динамики экипажа, приближенно принимается kДВ1 = 0,75 kДВ, где 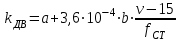 (8.4) (8.4)где а – коэффициент, равный для необрессоренных частей тележки а = 0,15; 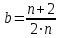 – коэффициент учитывающий влияние числа осей в группе тележек (n=2) под одним концом вагона на величину коэффициента динамики; – коэффициент учитывающий влияние числа осей в группе тележек (n=2) под одним концом вагона на величину коэффициента динамики;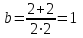 v – расчетная скорость движения, 33 м/с; fСТ– статический прогиб рессорного подвешивания, 0,068 м. 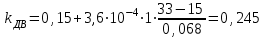 kДБК – расчетное значение коэффициента динамики боковой качки приближенно принимается kДБК = 0,25 ∙ kДВ; kДБК = 0,25 ∙ 0,245=0,06 Расчетное значение рамной силы 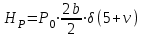 (8.5) (8.5)где Р0 – расчетная статическая осевая нагрузка; 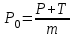 (8.6) (8.6)где m число колесных пар в вагоне, (m=4); 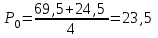 тс тс – коэффициент, учитывающий тип ходовых частей вагона, для грузовых вагонов на безлюлечных тележках с большой горизонтальной жескостью подвешивания = 0,003. 2b – расстояние между серединами шеек осей, для стандартных колесных пар 2b = 2,036 м; 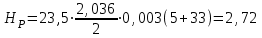 тс тсl – среднее расстояние между точками контакта колес с рельсами, принимается l =1,58 м; а1 = 0,220 м и а2 = 0,250 м – расчетные расстояния от точек контакта до середине шеек; r = 0,45 м – радиус средневзвешенного колеса. 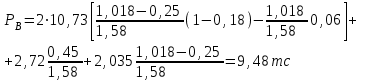 Приведенные параметра показаны на рисунке 3. 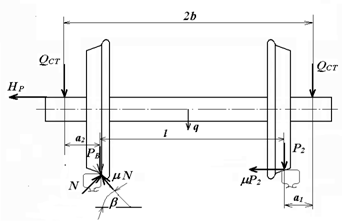 Рисунок 11 – Схема расчета устойчивости колес против схода с рельсов Боковое усилие взаимодействия гребня набегающего колеса и головки рельса (рисунок 16) вычисляется по формуле: 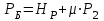 (8.7) (8.7)где 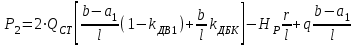 – вертикальная нагрузка от второго колеса на рельс; – вертикальная нагрузка от второго колеса на рельс;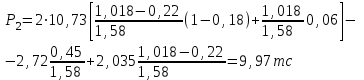 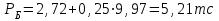 Подставим полученные значения вертикальной нагрузки от набегающего колеса на рельс и бокового усилия взаимодействия гребня и головки рельса в формулу (19): 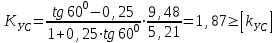 Коэффициент устойчивости по расчётам получен больше чем допускаемый, следовательно, колёсная пара тележки в кривой пути устойчива от вкатывания на головку рельса. 8.1 Определение величин нагрузок и схемы их приложенияСимметричность конструкции и нагрузки позволяет рассматривать одну половину боковой рамы, водя взамен отброшенной другой половины связи, в которых могут возникать только симметричные усилия – изгибающие моменты и продольные усилия (рисунок 12). 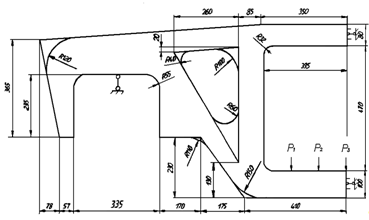 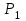 – нагрузка от одной двухрядной пружины; – нагрузка от одной двухрядной пружины;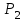 – нагрузка от двух двухрядных пружин; – нагрузка от двух двухрядных пружин;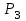 – половина нагрузки от одной двухрядной пружины. – половина нагрузки от одной двухрядной пружины.Рисунок 12 – Расчетная схема боковой рамы тележки 12-196-01 Величина нагрузки на нижний пояс буксового проема от одной двухрядной пружины определена в 5 пункте курсовой работы и составляет 30,495 кН. Для упрощения расчетов принимаем распределенную нагрузку. Тогда расчетная схема будет выглядеть, как показано на рисунке 18. 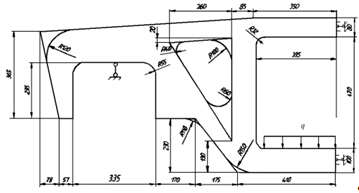 q – распределенная нагрузка на нижний пояс боковой рамы Рисунок 13 – Расчетная схема боковой рамы тележки 12-196-01 Распределенная нагрузка на нижний пояс половины боковой рамы будет рассчитано из условия, что в рессорном комплекте 7 пружин, но так как мы рассчитываем половину боковой рамы, то и нижний пояс будет воспринимать половину нагрузки: 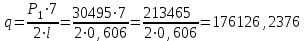 Н/м Н/м8.2 Исходные данные для расчетаНа основании чертежей и линейных размеров боковой рамы тележки модели 12-196-01 произведем аппроксимацию рассчитываемой боковой рамы в расчетную схему (рисунок 13). Материал принят изотропный линейно-упругий со сдедующимми свойствами: модуль упругости 2,1 ∙105МПа, коэффициент Пуассона 0,3, предел текучести 275МПа. Для построения сетки конечно-элементной модели боковой рамы тележки использован 10-узловой объемный нелинейный тетраэдр, обеспечивающий получение очень подробных и точных результатов расчета. Закрепление произведено по плоскости симетрии и в буксовом проеме. 8.3 Результаты расчета и их анализРезультаты расчета боковой рамы приведены на рисунке 14. 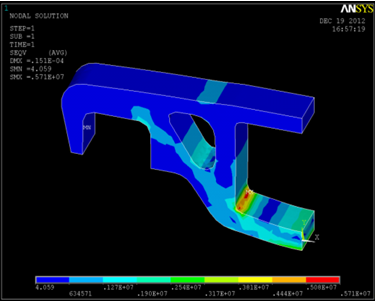 Рисунок 14 – Контурное распределение полей эквивалентный напряжений от воздействия вертикальной нагрузки Наибольшие напряжения 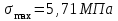 возникают в радиусе закругления нижнего пояса боковой рамы тележки. возникают в радиусе закругления нижнего пояса боковой рамы тележки.Сравним возникающие напряжения в боковой раме тележки с допускаемыми значениями напряжений для материала (сталь 20ГЛ), из которого сделана боковая рама тележки. Условие прочности выражается: 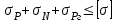 где 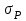 – расчетное напряжение на вертикальные нагрузки, МПа; – расчетное напряжение на вертикальные нагрузки, МПа;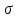 N – расчетное напряжение на продольные нагрузки, МПа; N – расчетное напряжение на продольные нагрузки, МПа;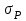 г-– расчетное напряжение на распорные нагрузки, МПа. г-– расчетное напряжение на распорные нагрузки, МПа.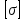 – допускаемое напряжение, МПа, ( – допускаемое напряжение, МПа, (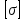 =0,9∙ =0,9∙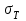 =0,9∙275=247,5 МПа (сталь 20ГЛ). =0,9∙275=247,5 МПа (сталь 20ГЛ).В результате расчета допускаемое напряжение равняется 247,5 МПа, полученное напряжение на вертикальные нагрузки составляет 5,71 МПа, что составляет 2,31 % от допускаемой величины. 9. Определение усилий, действующих на колесную пару в кривой пути и проверка запаса устойчивости колесной парыПримем суммарную нагрузку сосредоточенной в центрах элементов рессорного подвешивания. 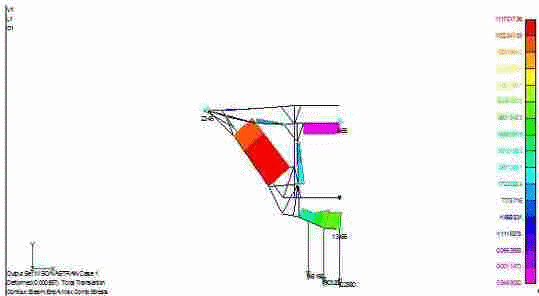 Рисунок 11 – Суммарные нагрузки Максимальное напряжение в боковой раме составляет примерно: σmax := 111,7 МПа Максимальное напряжение на эпюре возникает в наклонном нижнем поясе и имеет величину меньшую, чем допускаемое напряжение по I-му расчетному режиму. Это свидетельствует об обеспечении прочности этого элемента боковой рамы тележки под действием соответствующих нагрузок. Вывод по проведенным расчетам. Анализ напряженно-деформированного состояния боковой рамы тележки 18-100 под действием нагрузок, возникающих при эксплуатации ее под платформой с осевой нагрузкой 230.54 кН/ось, показывает обеспечение достаточной прочности конструкции от соответствующего нагружения. Следовательно, данная тележка может использоваться под заданным вагоном Список использованных источниковВагоны (конструкция, теория, расчет) /Под ред. Л.А. Шадура.-М.: Транспорт, 1980.-440 с. Вагоны/ И.Ф. Пастухов, В.В. Лукин, Н.И. Жуков.- М.: Транспорт, 1988.- 278 с. Габариты приближения строений и подвижного состава железных дорог колеи 1520 (1524) мм. ГОСТ 9238-83.- М.: Изд.- во стандартов, 1983.- 27 с. Конструирование и расчет вагонов / Под ред. В.В. Лукина.- М.: Изд.-во УМК МПС России, 2014.- 71 с. Глазкова И.В. Методические указания к лабораторным работам по дисциплине «Вагоны».- Иркутск: ИрИИТ, 2012.- 33 с. Нормы расчета и проектирования вагонов железных дорог МПС колеи 1520 мм (несамоходных)/ ГосНИИВ - ВНИИЖТ. М., 1996.- 319 с. Расчет вагонов на прочность / Под ред. Л.А. Шадура.-М.: Машиностроение, 1971.- 431 с. |
