ага реферат. 2 Реферат физика. Реферат Давление газа с точки зрения молекулярнокинетической теории. Уравнение состояния идеального газа.
 Скачать 0.9 Mb. Скачать 0.9 Mb.
|
|
Министерство сельского хозяйства Российской федерации Федеральное государственное бюджетное образовательное учреждение высшего образования Государственный университет по землеустройству Кафедра Высшей математики и физики Реферат «Давление газа с точки зрения молекулярно-кинетической теории. Уравнение состояния идеального газа.» Выполнил студент очной формы обучения Направление подготовки Городской кадастр 1 курса группы 11 ГК Данилова Анастасия Дмитриевна Преподаватель: Климов Александр Петрович Москва 2022 ОглавлениеМолекулярно-кинетическая теория 3 Дискретное строение вещества 5 Тепловое движение частиц вещества 6 Давление газа с точки зрения молекулярно-кинетической теории 7 Уравнение состояния идеального газа 12 Ссылки на источники 14 Молекулярно-кинетическая теорияМолекулярно-кинетическая теория (MKT) - теория, объясняющая свойства макроскопических тел и тепловые процессы в этих телах на основе представлений о веществе как о системе атомов и молекул, беспрерывно и хаотически движущихся и взаимодействующих друг с другом. Основные положения молекулярно-кинетической теории. В основе MKT лежат три положения: I положение: все вещества состоят из частичек — атомов и молекул. Существование атомов и молекул было предсказано еще древними философами. Однако ясную количественную теорию этого факта впервые предложил английский ученый-химик Джон Далтон (1766-1844). Составив таблицу относительных атомных масс ряда элементов, он заложил основу теории атомного строения вещества. В наше время, используя способность электронного микроскопа увеличивать в миллионы раз размеры объекта, можно увидеть и сфотографировать достаточно большие молекулы. II положение: частицы, из которых состоит вещество, находятся в непрерывного и беспорядочного (хаотического) движения. Верность этого положения была установлена на основе открытия, сделанного в 1827 году английским ботаником Робертом Броуном, наблюдавшим в микроскоп за движением цветочной пыльцы в воде. Он обнаружил, что пыльца совершает хаотическое движение и изменяет свое положение по сложной траектории (с). 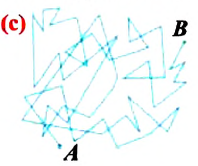 Беспорядочное движение частиц, называемое "броуновским движением", теоретически было объяснено А.Эйнштейном в 1905 году, а опытным путем было подтверждено в 1909-1911 годах французским физиком Яном Батистом Перреном (1870— 1942). Он подтвердил предположение Эйнштейна, что причиной хаотического движения частичек краски в воде является тепловое движение молекул воды. Перрен определил, что интенсивность броуновского движения частиц зависит не от их химической природы, а от температуры: с увеличением температуры интенсивность броуновского движения также увеличивается. Таким образом: Броуновским движением называется беспорядочное движение частиц, взвешенных в жидкости (или газе). Другим явлением, подтверждающим второе положение MKT, является диффузия. Диффузией называется процесс самопроизвольного взаимного проникновения атомов или молекул одного вещества в межатомные или межмолекулярные промежутки другого вещества. Первое количественнное описание процесса диффузии дал в 1855 году немецкий физик и физиолог Адольф Фик (1829-1901) в законе, названном "законом диффузии Фика ". III положение: частицы вещества взаимодействуют друг с другом, то есть между ними существуют силы взаимного притяжения и отталкивания. Подтверждением этого положения является возникновение силы упругости во время деформации тела. Эти силы имеют характер близкодействия, электромагнитную природу и в значительной степени зависят от расстояния между частицами. Например, было определено, что силы притяжения между молекулами уменьшаются по закону 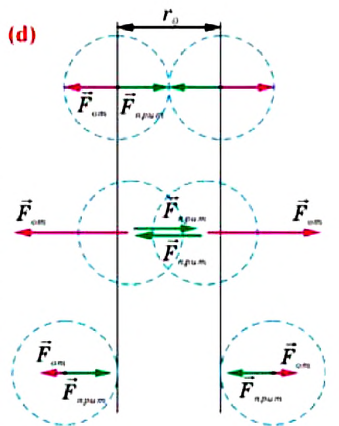 В основе молекулярно-кинетической теории лежат три положения: Вещество имеет дискретное строение, т. е. состоит из микроскопических частиц. Частицы вещества хаотически движутся. Частицы вещества взаимодействуют между собой. Дискретное строение веществаСогласно первому положению молекулярно-кинетической теории вещество имеет дискретное строение, т. е. состоит из отдельных частиц (молекул, атомов, ионов). При изучении физики в 6 и 8 классах вы узнали, что реальное существование молекул подтверждают экспериментальные факты. Такими фактами, в частности, являются растворение веществ в воде и в других растворителях, сжатие и расширение любых тел и особенно газов, механическое дробление вещества, диффузия, броуновское движение и многое другое. Глаз может различить две точки, если расстояние между ними не менее 0,1 мм. Современные оптические микроскопы позволяют различать структуры с расстоянием между элементами порядка двухсот нанометров и более (  фотография молекулы нуклеиновой кислоты нитевидной формы, общая длина которой 34 мкм. Переход от световых волн в оптических микроскопах к ускоренным пучкам электронов, управляемым электрическими и магнитными полями, в электронных микроскопах улучшил пределы разрешения до десятых долей нанометра. Использование электронных микроскопов позволило наблюдать и фотографировать атомарные структуры. 4 марта 1981 г. немецкий учёный Герд Бинниг и швейцарский учёный Генрих Рорер впервые в мире наблюдали отдельные атомы на поверхности кремния (рис. 3). На рисунке 4, а, б изображены электронный и туннельный микроскопы. За создание первого электронного микроскопа немецкому учёному Эрнсту Руске и за изобретение сканирующего туннельного микроскопа Г. Биннигу и Г. Рореру была присуждена Нобелевская премия по физике за 1986 год.  Тепловое движение частиц веществаСогласно второму положению молекулярно-кинетической теории частицы, составляющие вещество, находятся в непрерывном хаотическом движении, которое называют тепловым. Наиболее ярким экспериментальным подтверждением теплового движения частиц вещества (молекул, атомов и ионов) является броуновское движение, т. е. движение «взвешенных» в жидкости или газе мельчайших нерастворимых твёрдых частиц размерами примерно 1 мкм и меньше. «Взвешенные» частицы — это частицы, плотность вещества которых близка к плотности окружающей их среды (жидкости или газа). Они распределяются по всему объёму среды, не оседая на дно сосуда и не поднимаясь на её поверхность (рис. 5).  Давление газа с точки зрения молекулярно-кинетической теорииС точки зрения молекулярно-кинетической теории давление газа возникает в результате ударов молекул, образующих газ, по телу, соприкасающемуся с ним. При ударе импульс молекулы газа изменяется: средней силе продолжительностью При нормальных условиях и макроскопических размерах сосуда число ударов молекул газа о плоскую поверхность площадью 1 Пусть в сосуде, имеющем форму куба с ребром длиной l (рис. 12), находится идеальный газ, состоящий из одинаковых молекул массой Для описания удара молекулы газа о стенку ABCD (см. рис. 12) запишем соотношение (3.1) в проекциях на координатные оси: 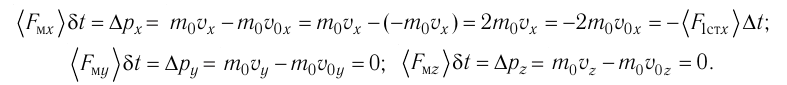 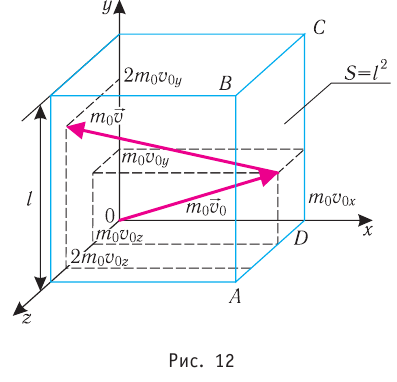 Так как промежуток времени между двумя последовательными соударениями молекулы со стенкой ABCD 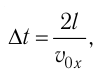 то то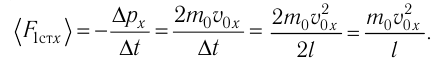 Проекция полной средней силы, с которой все N молекул, находящиеся в сосуде, действуют на стенку ABCD Следовательно, 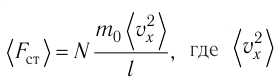 — усреднённый но всем N частицам квадрат проекций их скоростей на ось Ох. — усреднённый но всем N частицам квадрат проекций их скоростей на ось Ох.Разделив обе части соотношения для 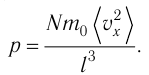 Так как 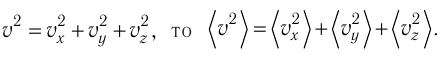 Поскольку молекулы газа совершенно одинаково отражаются от трёх пар противоположно расположенных граней куба, то Поскольку молекулы газа совершенно одинаково отражаются от трёх пар противоположно расположенных граней куба, то 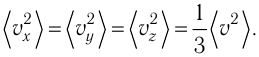 С учётом того, что занимаемый газом объём С учётом того, что занимаемый газом объём 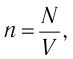 получим: получим: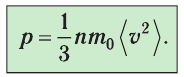 (3.2) (3.2)Уравнение (3.2) называют основным уравнением молекулярно-кинетической теории идеального газа. Это уравнение позволяет рассчитать макроскопический параметр давление р газа через концентрацию п молекул, массу т0 молекулы и среднюю квадратичную скорость её теплового движения, определяемую по формуле  Иначе говоря, формула (3.2) связывает между собой макро- и микроскопические параметры системы «идеальный газ». Иначе говоря, формула (3.2) связывает между собой макро- и микроскопические параметры системы «идеальный газ».Зависимость давления газа от среднего квадрата скорости движения его молекул объясняется тем, что с увеличением скорости, во-первых, возрастает импульс молекулы, а следовательно, и сила удара о стенку. Во-вторых, возрастает число ударов, так как молекулы чаще соударяются со стенками. Обозначим через  среднюю кинетическую энергию поступательного движения молекул. Тогда основное уравнение молекулярно-кинетической теории примет следующий вид: среднюю кинетическую энергию поступательного движения молекул. Тогда основное уравнение молекулярно-кинетической теории примет следующий вид: (3.3) (3.3)Из выражения (3.3) видно, что давление идеального газа зависит от средней кинетической энергии поступательного движения его молекул и их концентрации. Проиллюстрировать зависимость давления от скорости движения молекул газа можно, используя механическую модель. Соберём установку, изображённую на рисунке 13. Закрепим пластину П таким образом, чтобы она могла поворачиваться вокруг горизонтальной оси. Насыплем в воронку с узким горлышком мелкую дробь. Используя наклонный жёлоб, направим на пластину струйку дроби (дробинки играют роль молекул). В результате многочисленных ударов дробинок пластина отклонится на некоторый угол под действием силы давления дробинок. Увеличив высоту, с которой скатываются дробинки, а следовательно, и их скорость в момент удара о пластину, можно заметить, что пластина отклонилась на больший угол. Отсюда можно сделать вывод: чем больше скорость движения дробинок, тем больше производимое на пластину давление.  1. Идеальный газ — модель газа, удовлетворяющая следующим условиям: 1 ) молекулы газа можно считать материальными точками, которые хаотически движутся; 2) силы взаимодействия между молекулами идеального газа практически отсутствуют (потенциальная энергия взаимодействия равна нулю); они действуют только при столкновениях молекул, причём это силы отталкивания. 2. Уравнение, связывающее микронараметры состояния идеального газа (массу молекулы и её среднюю квадратичную скорость 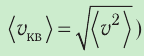 с его макропараметром (давлением, характеризующим газ как целое), непосредственно измеряемым на опыте, называют основным уравнением молекулярно-кинетической теории идеального газа: с его макропараметром (давлением, характеризующим газ как целое), непосредственно измеряемым на опыте, называют основным уравнением молекулярно-кинетической теории идеального газа: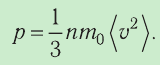 Давление идеального газа зависит от средней кинетической энергии поступательного движения его молекул и их концентрации: 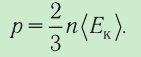 Уравнение состояния идеального газаУравнение состояния – устанавливает связь между параметрами состояния. В простейшем случае равновесное состояние тела определяется P, V, T. Связь между ними аналитически можно выразить так: F(P, V, T) = 0 где F – некоторая функция параметров. Это - уравнение состояния газа. При обычных условиях параметры состояния многих газов хорошо описываются уравнением 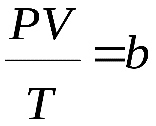 где b – константа, пропорциональная массе газа. Это уравнение выполняется точно для идеального газа. Идеальный газ – газ, молекулы которого не взаимодействуют друг с другом и имеют пренебрежимо малый объём. Молекулы соударяются друг с другом абсолютно упруго. Если ввести молярный объём 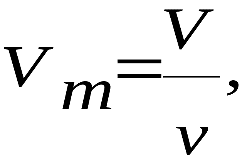 где ν – количество вещества и учесть, что где ν – количество вещества и учесть, чтоm = m0NAν =µν где m0 – масса одной молекулы. µ - молекулярная масса. NA – число Авогадро, то уравнение состояния можно записать в виде р Vm ν = b · T или PVm = RT * Согласно закону Авогадро при одинаковых давлениях и температурах молярные объёмы Vm различных газов одинаковы. (Vm = 22.4·10-3м3) при Н.У. Из этого закона и уравнения * следует, что постоянная R одинакова для всех газов. Это - универсальная газовая постоянная R = 8.31 Дж/(моль۰К) Для произвольной массы газа * * 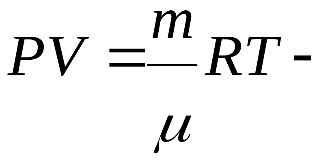 уравнение Менделеева Клапейрона, уравнение Менделеева Клапейрона,т.к. R = kNA , где k – постоянная Больцмана k = 1.38 · 10-23 Дж/К из ** получаем 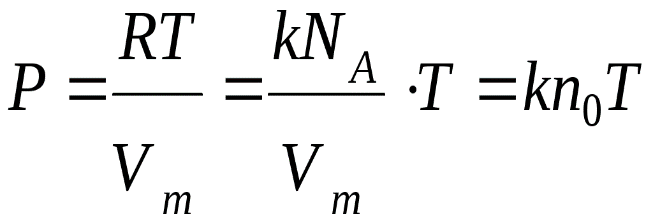 Р = kn0T Ссылки на источникиМолекулярно-кинетическая теория URL https://www.evkova.org/molekulyarno-kineticheskaya-teoriya#Основное%20уравнение%20молекулярно-кинетической%20теории%20идеального%20газа Давление газа с точки зрения молекулярно-кинетической теории URL https://studfile.net/preview/7195848/page:17/ Уравнение состояния идеального газа URL https://studfile.net/preview/7195848/page:17/ |
