реферат. Реферат Минимизация функции. Метод золотого сечения
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ ФЕДЕРАЛЬНОЕ ГОСУДРАТСВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» (ФГБОУ ВО «ВГУ») Факультет физический Кафедра радиофизики Реферат «Минимизация функции. Метод золотого сечения» Направление 03.03.03 Радиофизика Выполнила Голобородко Ю.О. Руководитель проф. Радченко Ю.С. Воронеж 2021г. Введение Применение необходимых и достаточных условий безусловного экстремума эффективно для решения ограниченного числа примеров, в которых вытекающие из условий соотношения имеют аналитическое решение. Для большинства практических задач они не могут быть рекомендованы по следующим причинам. Целевая функция 𝑓(𝑥)может не иметь непрерывных производных до второго порядка включительно. Использование необходимого условия первого порядка 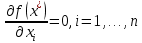 связано с решением системы nв общем случае нелинейных алгебраических уравнений, что представляет собой самостоятельную задачу, трудоемкость решения которой сравнима с трудоемкостью численного решения поставленной задачи поиска экстремума. связано с решением системы nв общем случае нелинейных алгебраических уравнений, что представляет собой самостоятельную задачу, трудоемкость решения которой сравнима с трудоемкостью численного решения поставленной задачи поиска экстремума.Возможны случаи, когда о целевой функции известно лишь то, что ее значение может быть вычислено с нужной точностью, а сама функция задана неявно. В зависимости от наивысшего порядка частных производных функции 𝑓(𝑥)численные методы решения задачи безусловной минимизации принято делить на 3 группы Методы нулевого порядка, использующие только информацию о значении функции 𝑓(𝑥). Методы первого порядка, использующие информацию о первых производных функции 𝑓(𝑥). Методы второго порядка, требующие для своей реализации знания вторых производных функции 𝑓(𝑥). Метод золотого сечения Постановка задачи Требуется найти безусловный минимум функции 𝑓(𝑥) одной переменной, т.е. такую точку 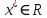 , что , что 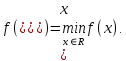 Для построения конкретного метода одномерной минимизации, работающего по принципу последовательного сокращения интервала неопределенности, следует задать правило выбора на каждом шаге двух внутренних точек. Конечно, желательно, чтобы одна из них всегда использовалась в качестве внутренней и для следующего интервала. Тогда число вычислений функции сократится вдвое и одна итерация потребует расчета только одного нового значения функции. В методе золотого сечения в качестве двух внутренних точек выбираются точки золотого сечения. Стратегия поиска Метод относится к последовательным стратегиям. Задается начальный интервал неопределенности и требуемая точность. Алгоритм уменьшения интервала опирается на анализ значений функции в двух точках. В качестве точек вычисления функции выбираются точки золотого сечения. Тогда с учетом свойств золотого сечения на каждой итерации, кроме первой, требуется только одно новое значение функции. Условия окончания процесса поиска стандартные: поиск заканчивается, когда длина текущего интервала неопределенности оказывается меньше установленной величины. Алгоритм метода Шаг 1. Задать начальный интервал неопределенности 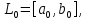 точность точность 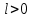 . .Шаг 2. Положить 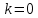 . .Шаг 3. Вычислить 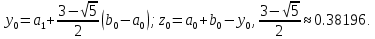 Шаг 4. Вычислить 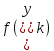 , ,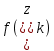 . .Шаг 5. Сравнить 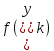 и и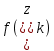 , ,А) если 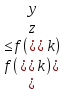 , то положить , то положить 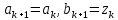 и и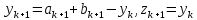 (рис. 1, а). Перейти к шагу 6 (рис. 1, а). Перейти к шагу 6Б) если  , положить , положить 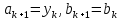 и и 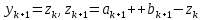 (рис. 1, б). (рис. 1, б).Шаг 6. Вычислить 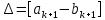 и проверить условие окончания: и проверить условие окончания:Если 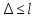 ,процесс поиска завершается и ,процесс поиска завершается и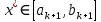 . В качестве приближенного решения можно взять середину последнего интервала: . В качестве приближенного решения можно взять середину последнего интервала: 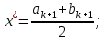 Если 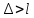 , положить , положить 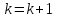 и перейти к шагу 4. и перейти к шагу 4. Рис.1 Пример 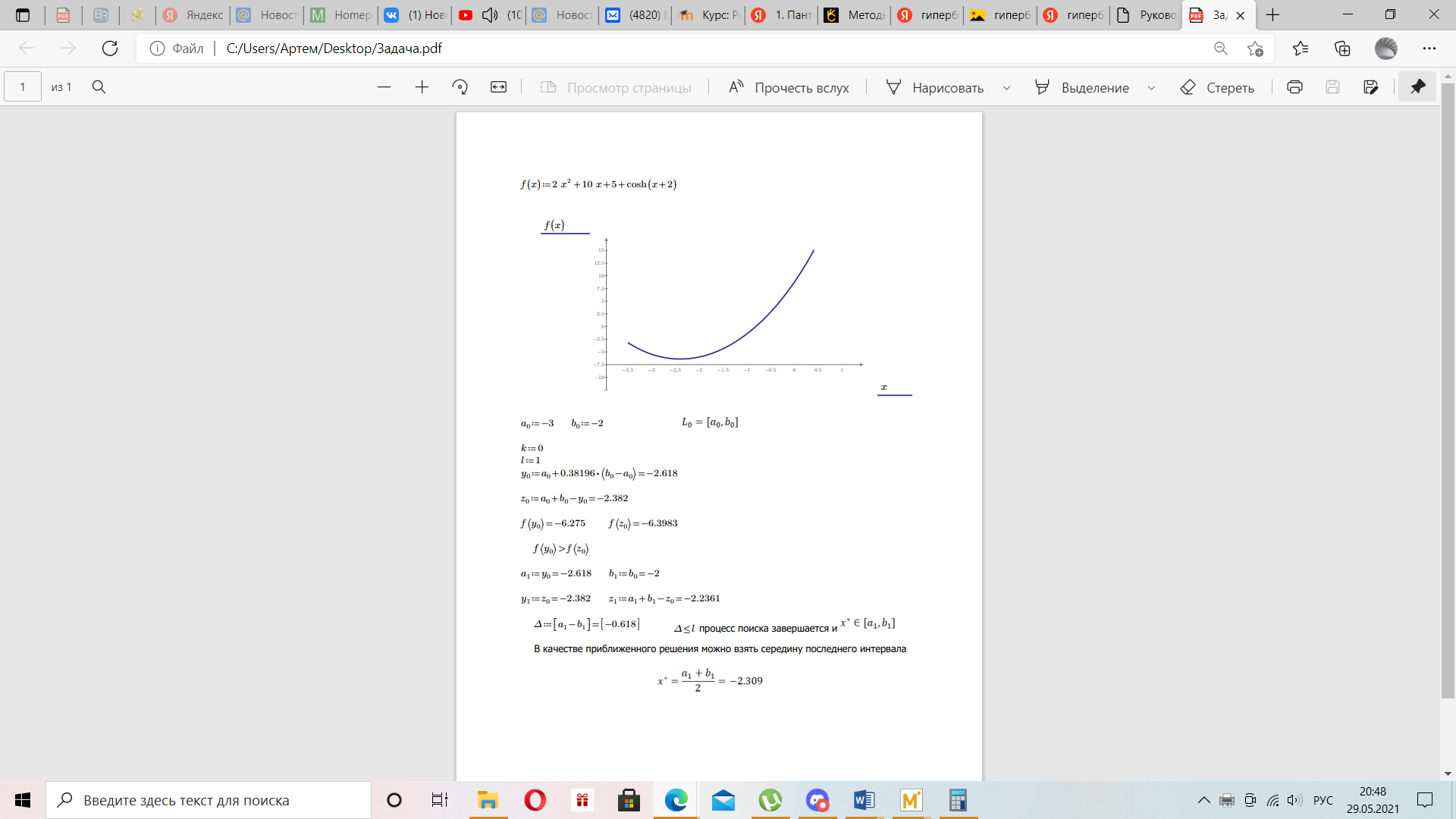 Список использованной литературы. Пантелеев А.В. Методы оптимизации в примерах и задачах / А.В. Пантелеев, Т.А. Летова /М:Высшая школа, 2002. – 544с. |
