хуета. Реферат на тему определение напряжений методом угловых точек работу

Название	Реферат на тему определение напряжений методом угловых точек работу
Дата	19.01.2023
Размер	2.91 Mb.
Формат файла
Имя файла	хуета.rtf
Тип	Реферат #895104

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

МОСКОВСКИЙ ИНФОРМАЦИОННО-ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ – МОСКОВСКИЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ ИНСТИТУТ

РЕФЕРАТ
на тему
ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ МЕТОДОМ УГЛОВЫХ ТОЧЕК

Работу выполнил

студент группы 02СТД4110

Е.Е.Уткин

Научный руководитель:

кандидат технических наук, доцент

А.Н. Громыко

г. Москва, 2023

Дисциплина «Механика грунтов» является частью группы дисциплин, связанных с проектированием, строительством и эксплуатацией зданий и сооружений, устройством подземных коммуникаций, прокладкой трубопроводов. Базовой дисциплиной по направлению «Строительство» для специальностей 27010265 «Промышленное и гражданское строительство» и 27010965 «Теплогазоснабжение и вентиляция» является «Механика грунтов», содержание которой определяется выпиской из Государственного Образовательного Стандарта Высшего Профессионального Образования. 5

Во многих случаях на выполнение работ нулевого цикла, включающих устройство оснований и фундаментов, затрачивается больше времени, чем на возведение сборных надземных конструкций зданий. Кроме того, стоимость этих работ иногда составляет до 40% от общей стоимости сооружений, поэтому их удешевление дает вполне ощутимый эффект. Надежность оснований и фундаментов и удешевление работ по их устройству в значительной степени зависят от умения правильно оценить инженерно-геологические условия площадок строительства, свойства грунтов в основаниях и совместную работу этих грунтов с деформирующимися фундаментами и конструкциями сооружения, от рациональности выбранных типов оснований, от качества выполнения работ. Механика грунтов изучает проблемы напряженно-деформированного состояния, прочности, деформативности и устойчивости грунтовых массивов и определяет условия их использования в качестве оснований объектов строительства 5

ГЛАВА 1. ОБЩИЕ СВЕДЕНИЯ О МЕТОДЕ УГЛОВЫХ ТОЧЕК 6

ГЛАВА 2. ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ МЕТОДОМ УГЛОВЫХ ТОЧЕК. ПОСЛЕДОВАТЕЛЬНОСТЬ 7

Рис.1 Схема к определению напряжений в грунте методом угловых точек 7

Проведем через точку О, взятую в центре большого прямоугольника, осевую вертикальную линию. Она будет также проходить через угловые точки О всех четырех малых прямоугольников. Если на этой вертикали взять на глубине z точку М₀, то осевое напряжение в ней от нагрузки, приложенной по площади большого прямоугольника, будет равно сумме угловых напряжений от нагрузки по площади четырех малых прямоугольников. Таким образом, угловое напряжение для каждого малого прямоугольника будет равно 1/4 величины осевого давления, возникающего на той же глубине от нагрузки по всей площади большого прямоугольника. Проведем через какую-либо угловую точку большого прямоугольника вертикальную линию и отметим на ней точку М, лежащую на глубине 2 z. Отношение этой глубины к ширине большого прямоугольника b будет равно отношению глубины z до точки М₀ к ширине малого прямоугольника b/2 . Так как относительная глубина точек М и М₀ для большого и малого прямоугольников одинакова, то и угловые напряжения в тех же точках будут равны между собой. 8

Следовательно, при нахождении напряжения s- под угловыми точками прямоугольной площади загружения значения коэффициента a можно принимать по табл. 3.4 в зависимости от h и x. В этом случае. Напряжения под угловыми точками определяют по формуле s_z= 0,25a×р 8

9

ЗАКЛЮЧЕНИЕ 12

ПЕРЕЧЕНЬ ЛИТЕРАТУРЫ 13

ВВЕДЕНИЕ

Механика грунтов — раздел физики грунтов и прикладной механики, описывающий поведение грунтов. Он отличается от механики жидкости и механики твердого тела тем, что почвы состоят из гетерогенной смеси жидкостей (обычно воздуха и воды) и частиц (обычно глины, ила, песка и гравия), но почва может также содержать органические твердые вещества и другие вещества.
Дисциплина «Механика грунтов» является частью группы дисциплин, связанных с проектированием, строительством и эксплуатацией зданий и сооружений, устройством подземных коммуникаций, прокладкой трубопроводов. Базовой дисциплиной по направлению «Строительство» для специальностей 27010265 «Промышленное и гражданское строительство» и 27010965 «Теплогазоснабжение и вентиляция» является «Механика грунтов», содержание которой определяется выпиской из Государственного Образовательного Стандарта Высшего Профессионального Образования. Во многих случаях на выполнение работ нулевого цикла, включающих устройство оснований и фундаментов, затрачивается больше времени, чем на возведение сборных надземных конструкций зданий. Кроме того, стоимость этих работ иногда составляет до 40% от общей стоимости сооружений, поэтому их удешевление дает вполне ощутимый эффект. Надежность оснований и фундаментов и удешевление работ по их устройству в значительной степени зависят от умения правильно оценить инженерно-геологические условия площадок строительства, свойства грунтов в основаниях и совместную работу этих грунтов с деформирующимися фундаментами и конструкциями сооружения, от рациональности выбранных типов оснований, от качества выполнения работ. Механика грунтов изучает проблемы напряженно-деформированного состояния, прочности, деформативности и устойчивости грунтовых массивов и определяет условия их использования в качестве оснований объектов строительства

ГЛАВА 1. ОБЩИЕ СВЕДЕНИЯ О МЕТОДЕ УГЛОВЫХ ТОЧЕК

1.1 Для определения напряжений в точках, не лежащих на оси симметрии площади загружения, используется метод угловых точек, предложенный в 1932 г. Д.Е. Польшиным. Он показал, что для любого равномерно загруженного прямоугольника угловое вертикальное напряжение на глубине 2z равно одной четверти осевого вертикального напряжения на глубине z.

Для точек, которые лежат ни нацентральной ни на угловой вертикалях применяют метод угловых точек.

Метод угловых точек для определения сжимающих напряжений применяют в тех случаях, когда грузовая площадь может быть разбита на такие прямоугольники, чтобы рассматриваемая точка оказалась угловой. Тогда сжимающее напряжение в этой точке (для горизонтальных площадок параллельных плоской границе полупространства) будет равно алгебраической сумме напряжений от прямоугольных площадей загрузки, для которых эта точка является угловой.

ГЛАВА 2. ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ МЕТОДОМ УГЛОВЫХ ТОЧЕК. ПОСЛЕДОВАТЕЛЬНОСТЬ

2.1. Метод определения напряжения методом угловых точек

Для определения связи между осевыми и угловыми напряжениями представим, что прямоугольная площадь загружения разделена на четыре равных прямоугольника, стороны которых в два раза меньше соответствующих сторон основного прямоугольника (рис.1)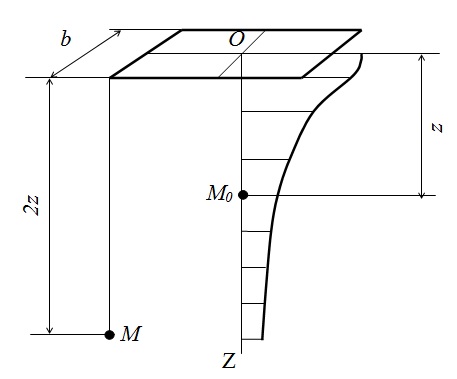

Рис.1Схема к определению напряжений в грунте методом угловых точек

Главное условие: Загруженные площадки разбиваются

на прямоугольники или достраиваются до прямоугольников так, чтобы расчетная точка являлась угловой для каждого из них.

Проведем через точку О, взятую в центре большого прямоугольника, осевую вертикальную линию. Она будет также проходить через угловые точки О всех четырех малых прямоугольников. Если на этой вертикали взять на глубине z точку М₀, то осевое напряжение в ней от нагрузки, приложенной по площади большого прямоугольника, будет равно сумме угловых напряжений от нагрузки по площади четырех малых прямоугольников. Таким образом, угловое напряжение для каждого малого прямоугольника будет равно 1/4 величины осевого давления,возникающегона той же глубине от нагрузки по всей площади большого прямоугольника. Проведем через какую-либо угловую точку большого прямоугольника вертикальную линию и отметим на ней точку М, лежащую на глубине 2 z. Отношение этой глубины к ширине большого прямоугольника b будет равно отношению глубины z до точки М₀ к ширине малого прямоугольника b/2 . Так как относительная глубина точек М и М₀ для большого и малого прямоугольников одинакова, то и угловые напряжения в тех же точках будут равны между собой. Следовательно, при нахождении напряжения s- под угловыми точками прямоугольной площади загружения значения коэффициента a можно принимать по табл. 3.4 в зависимости от h и x. В этом случае. Напряжения под угловыми точками определяют по формуле s_z= 0,25a×р
Метод угловых точек позволяет определять вертикальные напряжения s_z в любой точке полупространства при условии, что площадки являются прямоугольными, а нагрузки на них – равномерно распределенными. Для этого точку, в которой необходимо определить напряжение, с помощью дополнительных построений следует сделать угловой.

Если проекция рассматриваемой точки М’ находится в пределах загруженной площади (точка М), то эта площадь разделяется на четыре прямоугольника, для каждого из которых точка М является угловой (рис. 1.1,

а). Образуются прямоугольники: I – afMe, II – eMkd, III – fbhM, IV – Mhck. Тогда напряжения s_z найдем суммированием напряжений под угловыми точками четырех площадей загружения.

s_z = s_zI + s_zII + s_zIII +s_zIV = 0,25p(a_I + a_II + a_III + a_IV), где a_I , a_II , a_III , a_IV – коэффициенты, принимаемые по таблицам в зависи- мости от соотношения сторон площадей загружения I, II, III, IV и отношения z (глубины расположения точки М’) к ширине каждой из этих площадей.

Рис. 1.1 Схемы разбивки прямоугольной площади загружения при

определении напряжений методом угловых точек

а – точка М находится в пределах загруженной площади; б – точка М находится вне загруженной площади

Когда проекция рассматриваемой точки М΄ находится вне пределов загруженной площади, точку М можно представить как угловую для четырех фиктивных прямоугольников (рис. 1.1), б): I – afMe, II – eMkd, III – bfMh, IV – hMkc. При этом в пределах площадей III и IV нагрузку учитываем с отрицательным знаком. Тогда напряжения s_z найдем из выражения s_z = s_zI + s_zII - s_zIII -s_zIV = 0,25p(a_I + a_II - a_III - a_IV

Таким образом, пользуясь методом угловых точек, можно найти напряжение s_z в любой точке полупространства, к поверхности которого приложена равномерно распределенная по прямоугольной площадке нагрузка.

2.2 Пример выполнения

Определить напряжение в точке М на глубине z = 2,4 м, лежащей за пределами загруженной площади abcd. Размеры прямоугольной площади загружения: l = ab = cd = 4 м; b = ad = bc = 3 м. Расстояние точки М от грани ab – 1 м, от грани bc – 1 м. Интенсивность равномерной нагрузки р = 100 кПа.

Проведем построения, соответствующие рис 1.1, б. Получим фиктивные прямоугольники: I (afMe) с размерами l_I = 5 м, b_I = 1 м; II (eMkd) с размерами l_II =5 м, b_II = 2 м; III (bfMh) с размерами l_III = 1м, b_III = 1 м; IV (hMkc) с размерами l_IV = 2 м, b_IV = 1 м. Соотношение сторон в прямоугольнике I η_I = l_I /b_I = 5/1 = 5, коэффициент ξ_I = z/b_I = 2,4/1 = 2,4. В прямоугольнике II η_II = 5/2 = 2,5, ξ_II = 2,4/2 = 1,2; в прямоугольнике III η_III = 1/1 = 1, ξ_III = 2,4/1 = 2,4; в прямоугольнике IV η_IV = 2/1 = 2, ξ_IV = 2,4/1 = 2,4. Определим по табл. 3.4 значения коэффициентов a для соответствующих прямоугольников: a_I = 0,470; a_II = 0,741; a_III = 0,257; a_IV = 0,392. Тогда по формуле мы можем найти значение напряжения s_z в точке М:

s_z = 0,25p(a_I + a_II - a_III - a_IV) = 0,25·100·(0,47 + 0,741 – 0,257 – 0,392) =14 кПа.

ЗАКЛЮЧЕНИЕ

Метод угловых точек действительно помогает в определении

Напряжения в точках, не лежащих на оси симметрии. В данной работе я описал данный метод определения и порядок выполнения. Также в качестве примера я показал непосредственное решение задачи для большего понимания данного метода решения. Данный метод хорошо подойдет для расчета.

ПЕРЕЧЕНЬ ЛИТЕРАТУРЫ