Реферат по теории упругости(я сам не понял что писал). Реферат По дисциплине Экология
 Скачать 136.93 Kb. Скачать 136.93 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Российский Государственный Университет (НИУ) нефти и газа имени И. М. Губкина Факультет инженерной механики Реферат По дисциплине «Экология» «Экологические проекты Омской области в 21 веке. Проблема утилизации мусора» Выполнил студент: Группы МО-19-04 Шмаль Н. Е. Проверила: к.т.н. Орлова М. Н. Москва 2019 Оглавление ВВЕДЕНИЕ…………….………………..………………………………...... 2 Экологическая ситуация …..……………..…..…….……………………3 Виды отходов…………………………………………………..……… 3 Источники загрязнения………………………………………………5 Бытовые отходы…………………………………………..………….. 7 Экологические проблемы рек………………………….……………….. 9 2.1 Варианты улучшения водных объектов…………………………. 14 3. Варианты решения проблем……………..……..………………………...8 ЗАКЛЮЧЕНИЕ....…………………………..….....………………….……….10 СПИСОК ЛИТЕРАТУРЫ……………………………………………….……20 Введение В современной механике разрушения среди актуальных направлений исследований можно выделить следующие: получение оценки прочности конструкции и определение момента ее разрушения, прогнозирование первоначального направления развития трещины, влияние возникающих в окрестности ее вершины эффектов на процессы деформирования. Одним из важных аспектов оценки трещиностойкости материала является нахождение количественных характеристик распространения трещины, которая развивается под действием приложенных нагрузок, в частности, определение траектории ее распространения и определение первоначального направления роста. Критерии осреднения напряжений являются эффективными в задачах механики разрушения для анализа напряженно-деформированного состояния упругих материалов. В работе В.В. Новожилова [1] рассмотрены основные положения линейных и нелинейных подходов, кроме этого, сформулированы соответствующие критерии разрушения. Монографии В.А. Левина, Е.М. Морозова, Ю.Г. Матвиенко, В.З. Партона [2], [3] посвящены применению критерия прочности (критерии наибольшего главного напряжения, касательного, октаэдрического напряжения) в зависимости от типа используемых материалов, что позволяет провести дальнейший анализ условий эксплуатации конструкций. Л.В. Степанова, С.А. Бронников, О.Н. Белова в статье «Оценка направления роста трещины в условиях смешанного нагружения» подробно описывают методику определения первоначального направления развития произвольно ориентированной трещины с помощью обобщенных критериев, которые используются в современной механике разрушения для моделирования, выполненного численными методами [4]. В ряде работ отечественных и зарубежных ученых анализируется постановка критерия осредненных напряжений вблизи вершины трещины для нахождения начального направления страгивающейся трещины при смешанных условиях нагружения, а также статистическая обработка соответствующих экспериментальных данных задачи [5], [6]. Локальный критерий максимального тангенциального напряжения, который является одним из универсальных критериев, описан в работах Ю.Г. Матвиенко [7]. 1 Определение начального направления развития трещины Рассмотрим локальный критерий начального направления роста трещины на основе принципа критерия максимальных осредненных напряжений в зоне процесса разрушения в окрестности конца трещины. Воспользуемся выражениями для тангенциальных напряжений [8] для решения задачи о напряженно-деформированном состоянии пластины, содержащей прямолинейную трещину. Эти выражения необходимы для определения начального направления распространения трещины при нагружении смешанного типа. С целью исследования основных закономерностей деформирования пластины в окрестности вершины трещины при растягивающей нагрузке используем аналитическое решение упругой задачи. Построим математическую модель для задачи о растяжении пластины, ослабленной прямолинейной трещиной [9]. Бесконечную плоскость заменим квадратом достаточно большого размера. Его размеры будем выбирать так, чтобы была возможной замена бесконечной области конечной, а начало системы координат направим в точку пересечения его диагоналей. Известно, что при удалении от края прямолинейной центральной трещины на величину, равную половине длины трещины, концентрация напряжений быстро уменьшается. В задачах теории упругости и пластичности учитывается факт: если ширина пластины превышает на порядок длину трещины, то разница в решениях по наиболее чувствительному компоненту тензора напряжений σθθ, представленному в полярной системе, не превысит 6% [10]. Объектом данного численно-аналитического исследования служила пластина высотой 200 мм, длиной 200 мм с центральной прямолинейной трещиной длиной a = 20 мм. Плоский образец представляем в виде пластины как приближение пространственного образца с малой толщиной. Его ширина сечения W образца удовлетворяет следующему соотношению: a 0,6*W, в данном случае W можно взять равным 10 мм. Зададим на границе рассматриваемого квадрата напряжения, соответствующие одноосному растяжению пластины в 70 МПа. Связь между полярной и декартовой системами координат осуществляется по следующим формулам: 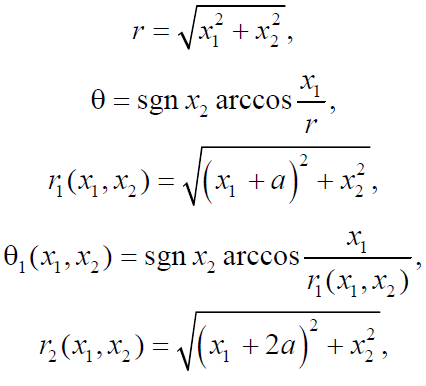 где (x1, x2), (r, θ) – координаты текущей точки в декартовой и полярной системе координат соответственно. На рисунке 1.1 представлены основные числовые параметры углов, напряжений и расстояний до текущей точки, которые используются при решении задачи в окрестности вершины трещины. 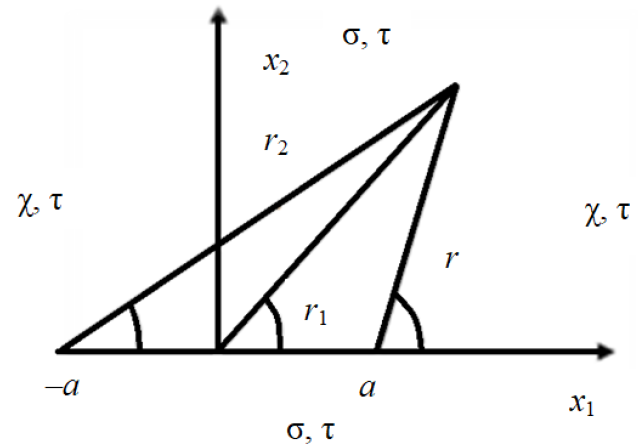 Рисунок 1.1 – Система координат в окрестности вершины трещины На рисунке 1.1 можно выделить следующие обозначения углов: θ1 – это угол между r1 и осью абсцисс; θ2 – это угол между r2 и осью Ox; θ – это угол между r и осью абсцисс, σ, τ, χ – напряжения, приложенные к границам пластины. Тогда компоненты тензора напряжений выражаются формулами [11]: 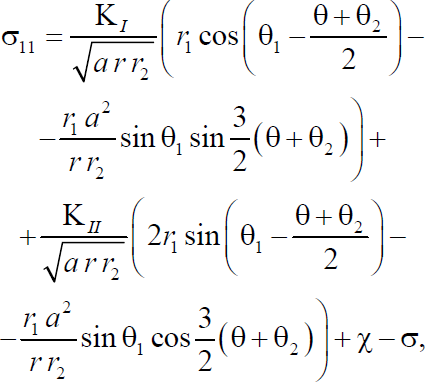 где коэффициенты интенсивности выражаются через значения напряжения следующим образом: 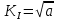 , , 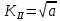 Тогда выразим компоненты тензора напряжений в полярной системе по формулам: Формулы связи декартовой системы координат и полярной системы представлены следующими соотношениями: Учитывая предыдущие соотношения, выразим компонент тензора напряжений 11 в зависимости от параметров углов, исходных напряжений на границе и расстояний до текущей точки: Компонент тензора напряжений 22 , учитывая значения коэффициентов интенсивности, примет вид: Тогда можно оценить размеры области предразрушения вблизи вершины страгивающейся трещины по следующей формуле: где величина σ0 – это предельные локальные напряжения, действующие в зоне предразрушения, коэффициент K1c – вязкость разрушения; Согласно критерию максимальных осредненных тангенциальных напряжений, первоначальный рост трещины совершается в том направлении, где достигается наибольшее значение компонента тензора напряжений σθθ. Запишем критерий в следующем виде [1]: 2 Результаты расчетов На рисунках 2.1, 2.2 представлены графики компонента тензора напряжений σθθ для трещины в случае нормального отрыва. Проанализировав полученный график, можно сделать вывод о наличии двух локальных максимумов функции σθθ, которые достигаются при значениях углов θ = ±1,96 (рад). Предположительно в одном из этих направлений начнется первоначальный рост трещины. На рисунке 2.2 видно, что подрастание привело к перераспределению напряжений в привершинной области и изменению направления дальнейшего роста трещины. Локальный максимум достигается при θ = ±2,36 рад. Знак угла выбирается с учетом предыдущих подрастаний трещины. Построим зависимость направления развития трещины от расстояния до вершины трещины (рисунок 2.3). Проанализировав полученный график, можно сделать вывод, что в непосредственной окрестности вершины трещины первоначальное направление ее дальнейшего развития совпадает с осью, на которой расположена прямолинейная трещина θ 0, что согласуется с известными результатами [11]. Также требует учета тот факт, что при малейшем продвижении трещины происходит перераспределение напряжений в окрестности ее вершины и значение угла требуется пересчитывать. Запишем зависимость интенсивности напряжений в полярной системе координат (при условии плоской деформации) в зависимости от угла θ: График данной функции представлен на рисунке 2.4 для расстояния от вершины трещины, составляющем 20% ее длины, при исходном напряжении 1,6 МПа (материал мрамор). По графику видно, что интенсивность напряжений принимает максимальное значение не при θ = 0, а при значении θ = / 4. Этот же Заключение На протяжении всей истории человечества отходы жизнедеятельности были неотемлемой частью существования цивилизации. Можно сказать, что все мы живем на слое отходов предыдущих поколений. Однако в последние десятилетия резко изменились количество качество отходов. Если раньше все отходы разлагались с течением времени естественным путем, то многие современные отходы, те же пластмассовые бутылки, при обычной утилизации не разлагаются и через тысячу лет. А при низкотемпературном сжигании выделяют в атмосферу вредные вещества. К тому же лимит природных ресурсов ограничен, поэтому весь мир идёт к полному использованию отходов. В развитых странах при переработке отходов стремятся воспроизвести природный цикл, а мы, из-за своей бедности и относительного изобилия ресурсов, перекладываем проблему загрязнения окружающей среды на плечи следующих поколений. Несмотря на огромные масштабы, проблема утилизации отходов решаема. Конечно, каждый житель планеты должен начинать борьбу с себя. Но всё же сознание людей должно быть обязательно подкреплено мерами, принятыми на государственном уровне. Необходимо создание всеобъемлющей системы, занимающейся вопросами ответственного обращения с ресурсами природы и утилизации отходов. Только комплексный подход к проблеме со стороны государства, местных властей, а также каждого отдельно взятого жителя планеты может свести к минимуму риски губительного воздействия отходов на экосистему. Список литературы: Голубев И.Р. О мониторинге "здоровье - окружающая среда" / И.Р. Голубев // Гигиена и санитария. - 2001. - № 4. - 66-68. Другов Ю.С. Анализ загрязненной почвы и опасных отходов / Ю.С. Другов, А.А. Родин. - М.: Бином. Лаборатория знаний, 2007. - 424 с. Охрана окружающей среды в Омской области : стат. сб. / ред. А. А. Агеенко. - Омск : Омскстат, 2008. - 36 с. Состояние и охрана окружающей среды Омской области в 2003 году : докл. / ред. Н.Н. Яловенко. - Омск : б. и.., 2004. - 331 с. 20.1 С 66 http://www.omsk.mid.ru/obsh_inf.html http://s99-omsk.narod.ru/teachers/nou/biolog.htm http://infomsk.ru/news/ekologicheskie_taynyi_neftezavoda/ http://www.omsktfi.ru/nature/natconditions.html http://www.omsktfi.ru/literature/articleslit/149-a18.html http://www.bereg-omsk.ru/Yekologicheskie_problemy_r_Irtysh-3.html |
