Математическая логика реферат 2023 год (1). Реферат по дисциплине Логика и основы алгоритмизации студент гр. 21ИВ1бз Бакулин М. Д
 Скачать 1.7 Mb. Скачать 1.7 Mb.
|
|
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Пензенский государственный технологический университет» (ПензГТУ) Факультет автоматизированных информационных технологий Кафедра «Программирование» Реферат по дисциплине: «Логика и основы алгоритмизации» Выполнил: студент гр. 21ИВ1бз Бакулин М.Д. Принял: ассистент кафедры «Программирование» Зоткина А.А. г. Пенза, 2023 г. Содержание:
1 Основные понятия о графах Объектом исследований теории графов является «граф», который определяется следующим образом. Граф - это топологическая модель, которая состоит из множества вершин и множества соединяющих их рёбер. При этом значение имеет только сам факт, какая вершина с какой соединена. Приведем пример графа, состоящего из 8 вершин и 8 ребер. Данный граф показан на рисунке 1.1.  Рисунок 1.1 – Заданный граф Следующим шагом необходимо разобраться с такими понятиями как: вершина и ребра графа. Вершина - точка в графе, отдельный объект, для топологической модели графа не имеет значения координата вершины, её расположение, цвет, вкус, размер; однако при решении некоторых задачах вершины могут раскрашиваться в разные цвета или сохранять числовые значения. Ребро - неупорядоченная пара двух вершин, которые связаны друг с другом. Эти вершины называются концевыми точками или концами ребра. При этом важен сам факт наличия связи, каким именно образом осуществляется эта связь и по какой дороге - не имеет значения; однако рёбра может быть присвоен «вес», что позволит говорить о «нагруженном графе» и решать задачи оптимизации. Следующими не мало важными терминами, которые относятся к понятию графа нужно отнести: Инцидентность - вершина и ребро называются инцидентными, если вершина является для этого ребра концевой. Обратите внимание, что термин «инцидентность» применим только к вершине и ребру. Смежность вершин - две вершины называются смежными, если они инцидентны одному ребру. Смежность рёбер - два ребра называются смежными, если они инцедентны одной вершине. Говоря проще - две вершины смежные, если они соединены ребром, два ребра смежные - если они соединены вершиной. Данные характеристики графа приведены на рисунке 1.2.  Рисунок 1.2 – Характеристики графа Рисунок 1.2 – Характеристики графаПетля - ребро, инцидентное одной вершине. Ребро, которое замыкается на одной вершине. Псевдограф - граф с петлями. С такими графами не очень удобно работать, потому что, переходя по петле мы остаёмся в той же самой вершине, поэтому у него есть своё название. Данные характеристики показаны на рисунке 1.3. 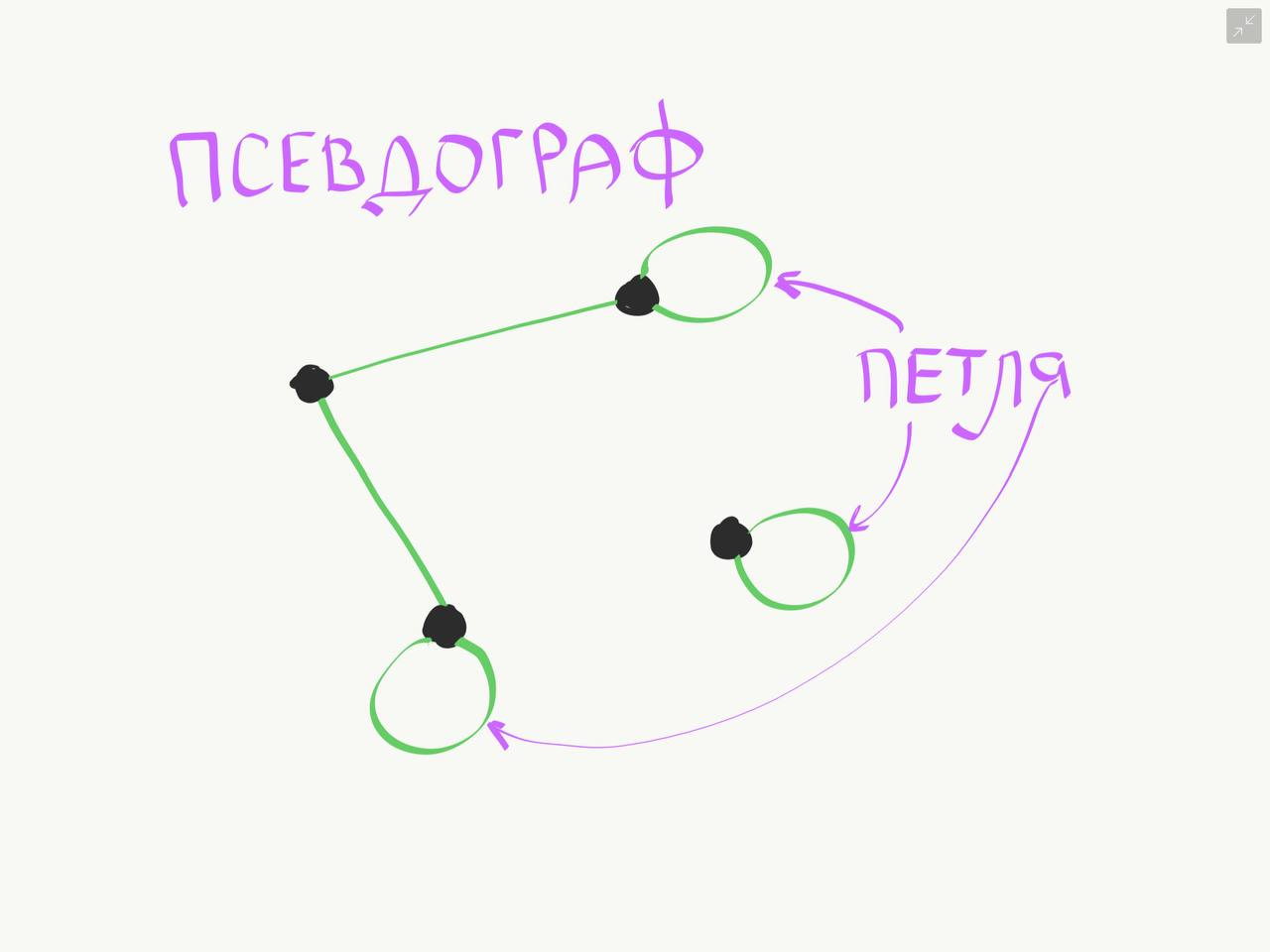 Рисунок 1.3 – Характеристики графа Степень вершины - это количество рёбер, инцидентных указанной вершине. По-другому - количество рёбер, исходящих из вершины. Петля увеливает степень вершины на 2. Изолированная вершина - вершина с нулевой степенью. Висячая вершина - вершина со степенью 1. Данные характеристики показаны на рисунке 1.4. 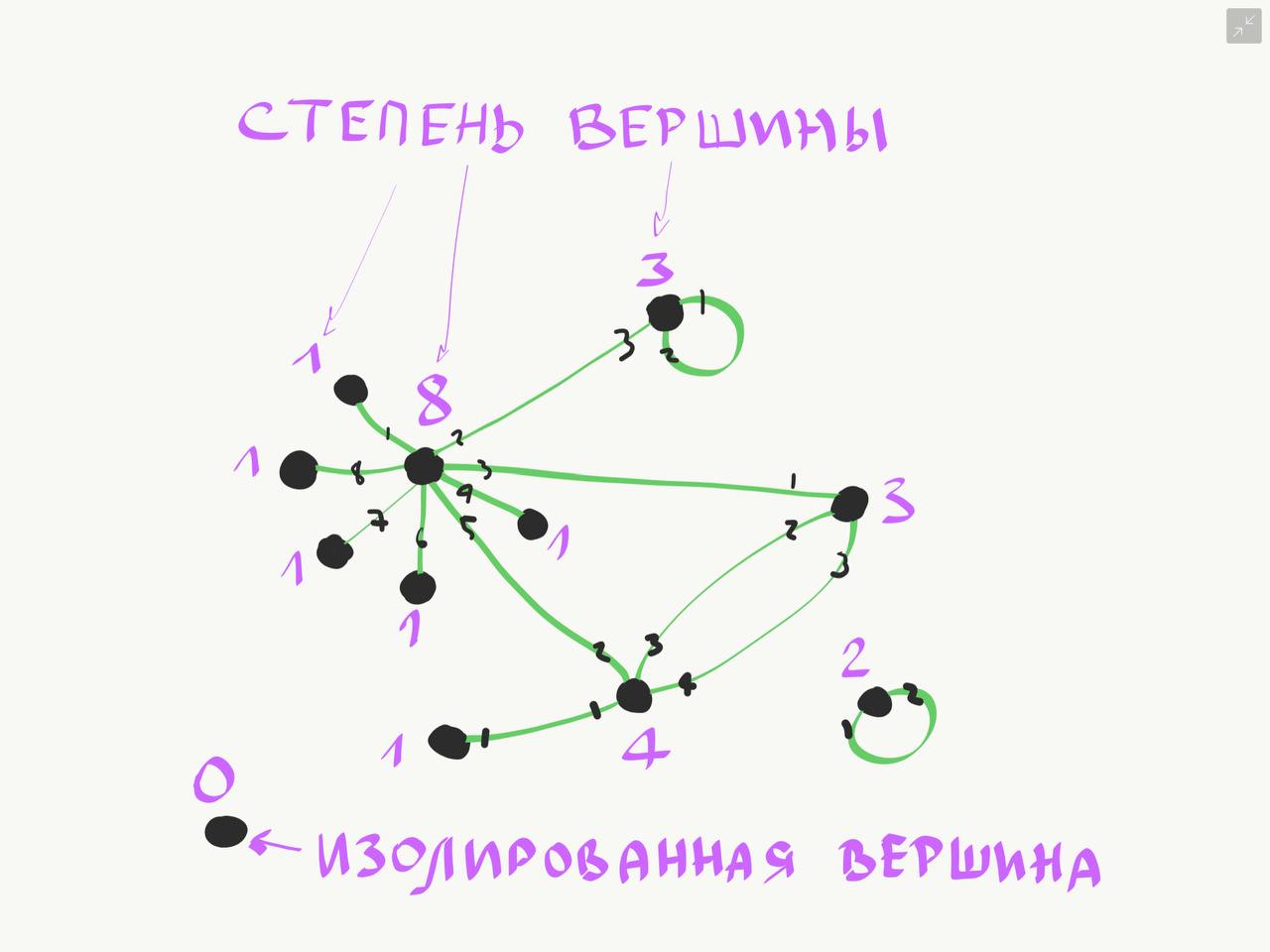 Рисунок 1.4 – Характеристики графа После того как мы познакомились с основными составными частями графа, необходимо разобраться, а какие существуют графы. Разберемся с основными видами графов. Полный граф - это граф, в котором каждые две вершины соединены одним ребром. Данный граф показан на рисунке 1.5. 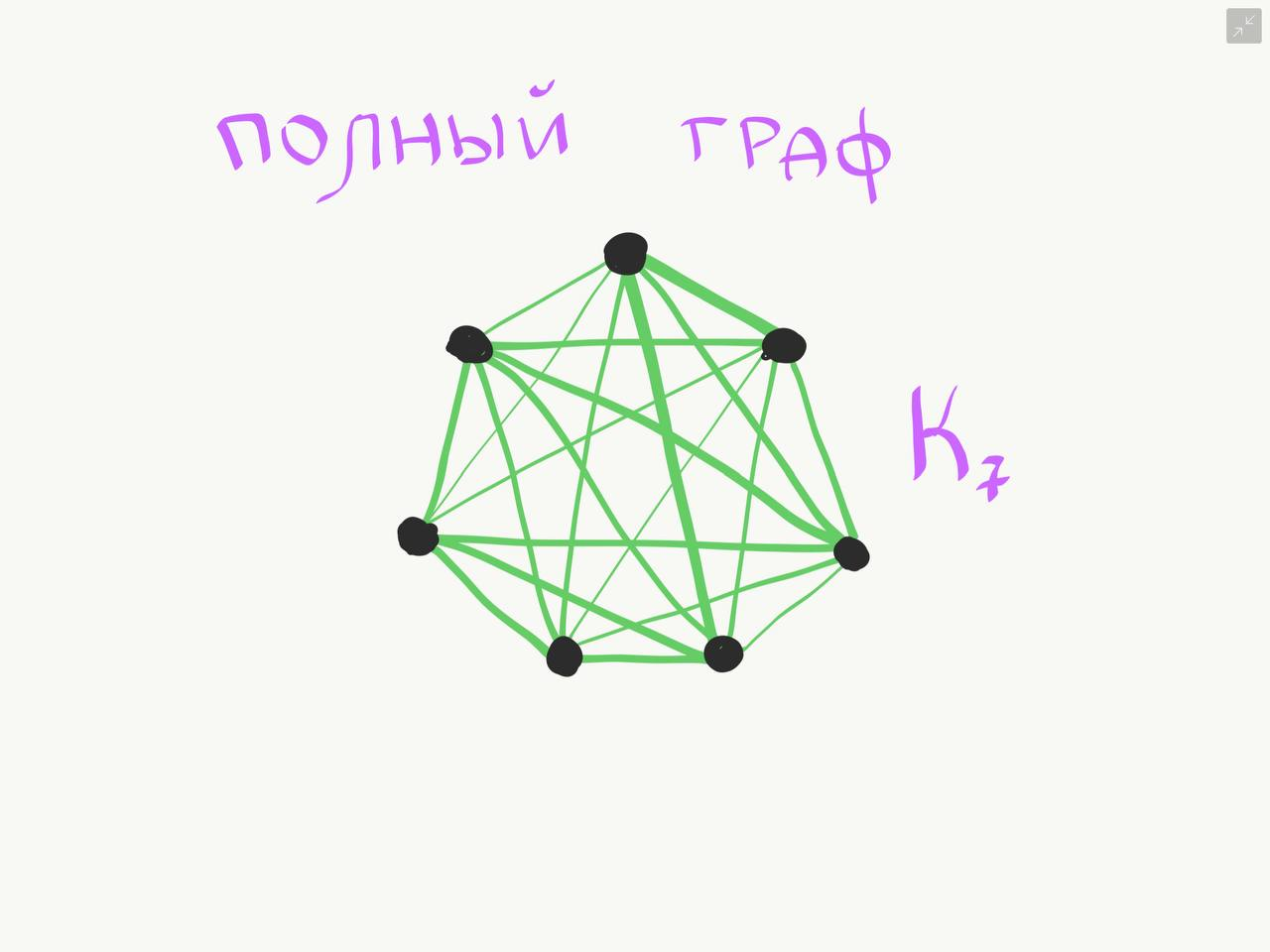 Рисунок 1.5 – Полный граф Рисунок 1.5 – Полный графРегулярный граф - граф, в котором степени всех вершин одинаковые. Данный граф показан на рисунке 1.6. 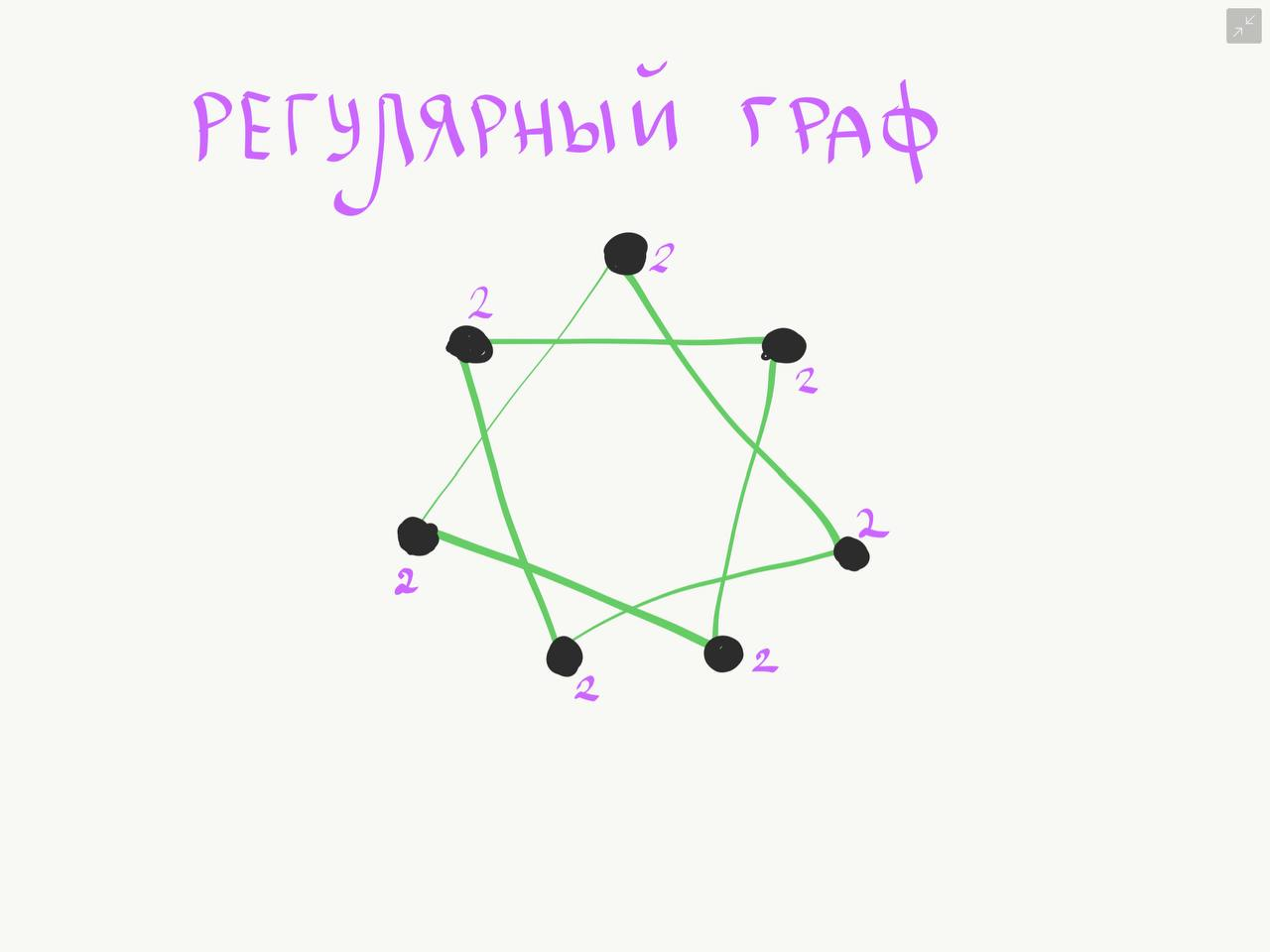 Рисунок 1.6 – Регулярный граф Двудольный граф - если все вершины графа можно разделить на два множества таким образом, что каждое ребро соединяет вершины из разных множеств, то такой граф называется двудольным. Например, клиент-серверное приложение содержит множество запросов (рёбер) между клиентом и сервером, но нет запросов внутри клиента или внутри сервера. Данный граф показан на рисунке 1.7. 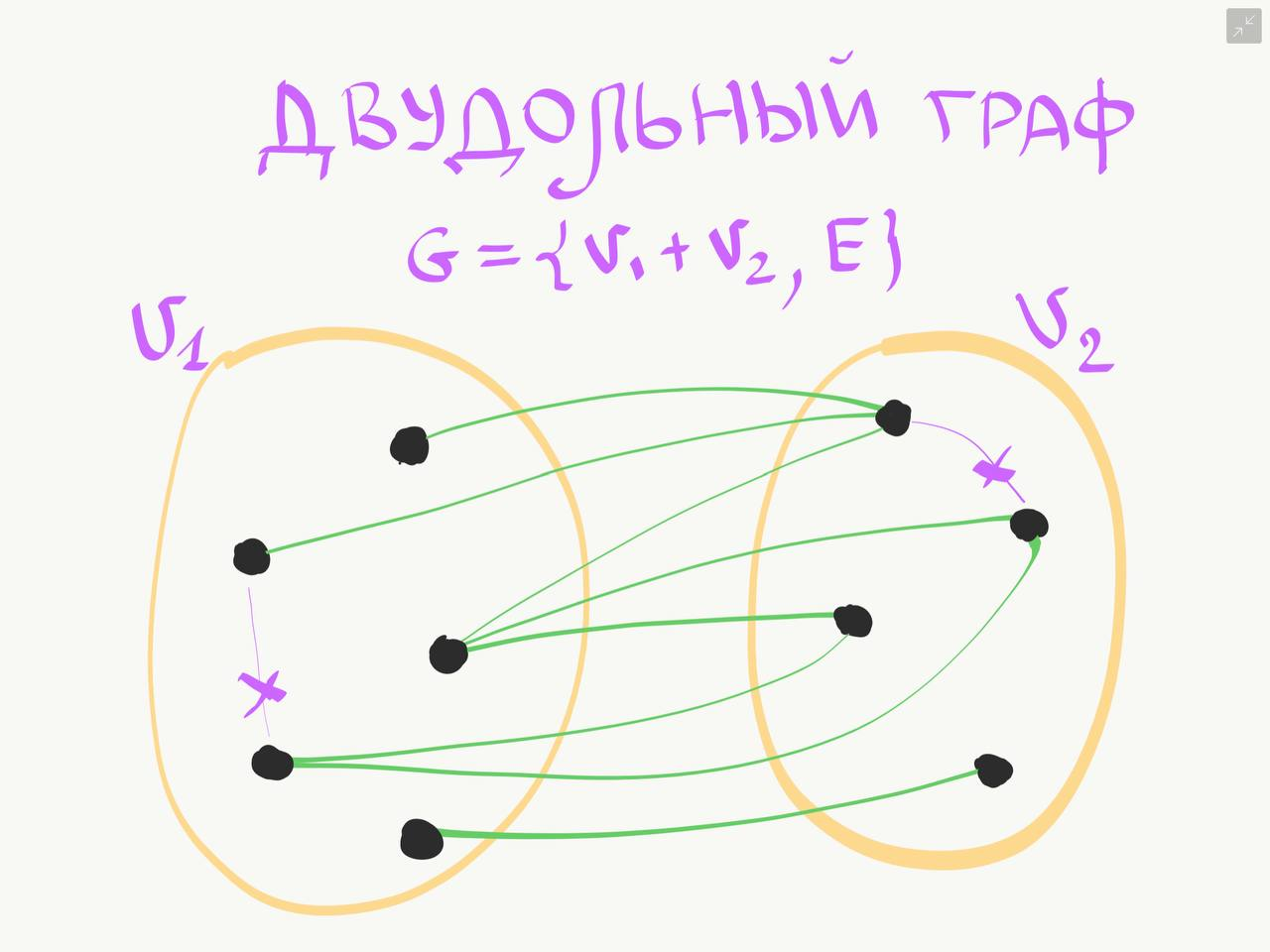 Рисунок 1.7 – Двудольный граф Планарный граф. Если граф можно разместить на плоскости таким образом, чтобы рёбра не пересекались, то он называется «планарным графом» или «плоским графом». Данный граф показан на рисунке 8. 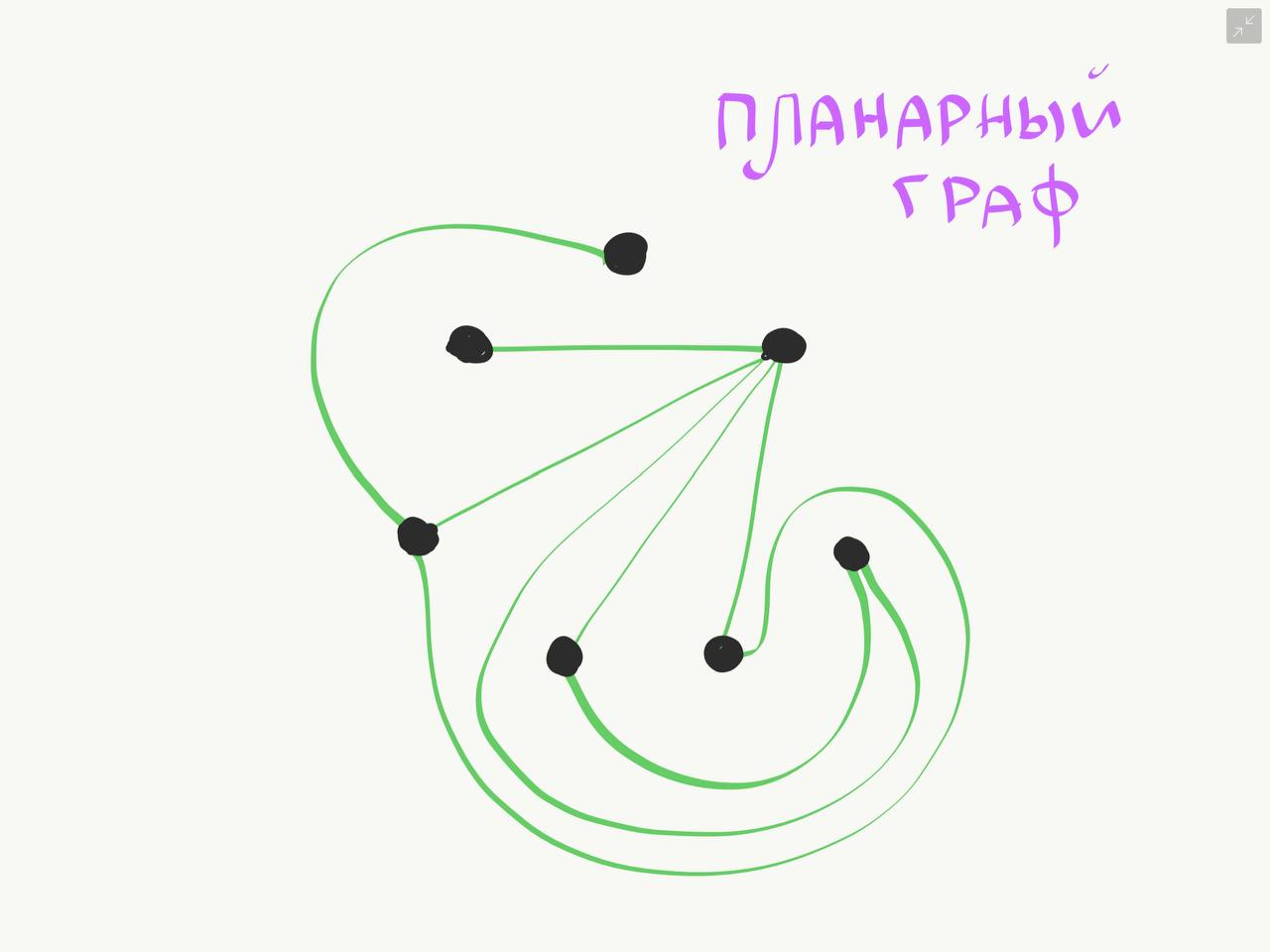 Рисунок 1.8 – Планарный граф На основании этих графов можно построить вариации других графов. 2 Способы задания графов Существует много способов представить граф, назовем только самые распространенные. Все они иллюстрируются на примере одного графа. Перечисление элементов. Исходя из определения, для того, чтобы задать граф, достаточно перечислить его вершины и ребра (т.е. пары вершин). 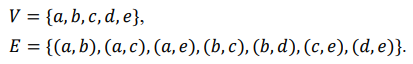 Изображение. Если граф не слишком большой, его можно нарисовать. В неориентированном графе ребра изображают линиями, соединяющими смежные вершины, в ориентированном – стрелками. На рисунке 2.1 показан граф, заданный выше перечислением вершин и ребер. 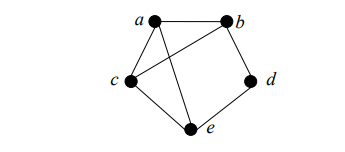 Рисунок 2.1 – Изображение графа Матрица смежности. Пусть – граф с вершинами, пронумерованными числами от 1 до n. Матрица смежности – это таблица с n строками и n столбцами, в которой элемент, стоящий на пересечении строки с i номером и столбца с номером j, равен 1, если вершины с номерами i и j смежны, и 0, если они не смежны. Пример (вершины пронумерованы в алфавитном порядке, рисунок 2.2.) 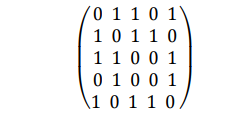 Рисунок 2.2 – Матрица смежности На главной диагонали матрицы смежности обыкновенного графа всегда стоят нули (нет петель) и эта матрица симметрична относительно главной диагонали (граф неориентированный). Матрица инцидентности. Пусть – граф, вершины которого пронумерованы числами от 1 до n, а ребра – числами от 1 до m. В матрице инцидентности строки соответствуют вершинам, а столбцы – ребрам. На пересечении строки с номером i и столбца с номером j стоит 1, если вершина с номером i инцидентна ребру с номером j и 0 в противном случае (Рисунок 2.3.). 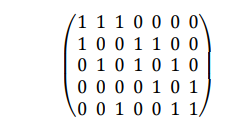 Рисунок 2.3 – Матрица инцидентности Списки смежности. Этот способ часто используется для компьютерного представления графов. Состоит он в том, что для каждой вершины задается список всех смежных с ней вершин. В структурах данных, применяемых в программировании, списки смежности могут быть реализованы как массив линейных списков. В формулировках задач будем эти списки оформлять так: пишется номер или имя вершины и после двоеточия перечисляются все смежные с ней вершины. Пример данного способа приведен на рисунке 2.4. 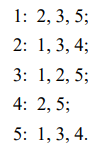 Рисунок 2.4 – Списки смежности 3 Операции над множествами Для того чтобы разобраться с операциями над множествами вспомним, что такое множество. Множество — одно из основных понятий современной математики. Это понятие не сводится к другим понятиям и не определяется. Вместо определения приведем несколько примеров множеств: 1) множество действительных чисел; 2) множество точек плоскости; 3) множество букв русского алфавита; 4) множество деревьев в лесу; 5) множество учащихся данного класса. Первой операцией над множествами будет: Пересечение множеств. Пусть даны два множества А и В. Пересечением (произведением) множеств А и В называется множество, состоящее из всех элементов, принадлежащих одновременно и множеству А, и множеству В. Обозначают пересечение множеств. A ∩ B. A ∩ B = {х | х ∈ A и х ∈ B}. Аналогично определяется пересечение любого числа множеств. Графически удобно пересечение множеств изображать в виде общей части двух или более кругов Эйлера–Венна (рисунок 3.1). 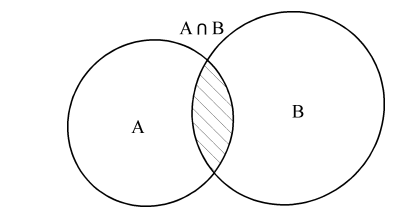 Рисунок 3.1 – Пересечение множеств А = {2n | n ∈ N} — множество чисел, делящихся на 2, B = {3n | n ∈ N} — множество чисел, делящихся на 3, тогда A ∩ B = {6n | n ∈ N} — множество чисел, делящихся на 6. А — отрезок [0; 5], В — отрезок [2; 7], тогда A ∩ B — отрезок [2; 5]. Следующей операцией будет операция объединения. Объединением двух множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В. Обозначают объединение множеств A ∪ B (рис. 3.2).  Рисунок 3.2 – Объединение множеств A ∪ B = {х | х ∈ A или х ∈ B}. Аналогично определяется объединение любого числа множеств. Разностью множеств А и В, называется множество, состоящее из всех элементов, множества А, не принадлежащих множеству В. Обозначают разность множеств A \ B (рис. 3.3). A \ B = {х | х ∈ A и х ∉ B}. 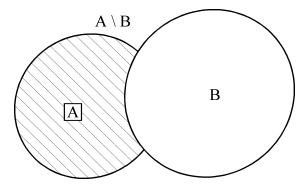 Рисунок 3.3 – Разность множеств Симметрической разностью множеств А и В, называется множество, состоящее из всех элементов, принадлежащих только одному множеству А или В, обозначают A Ì B (рис. 3.4). 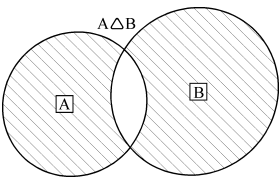 Рисунок 3.2 – Симметрическая разность множеств |
