Законы распределения. Галаева Б8213 реферат. Реферат по дисциплине Математические методы в экологии

• Название: Реферат по дисциплине Математические методы в экологии
• Анкор: Законы распределения
• Дата: 26.05.2020
• Размер: 137.61 Kb.
• Имя файла: Галаева Б8213 реферат.docx
• Тип: Реферат; #125557

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение
высшего образования

«Дальневосточный федеральный университет»

ШКОЛА ЕСТЕСТВЕННЫХ НАУК

Кафедра экологии

РЕФЕРАТ

по дисциплине «Математические методы в экологии»

Специальность 05.03.06 «Экология и природопользование»

на тему «Законы распределения»

Выполнил студент гр.Б8213 Галаева А. И.

Владивосток

2019

Оглавление

1.Биноминальное распределение 3

2.Распределение Пуассона 4

3.Нормальное распределение 6

4.Распределение Максвелла 7

5.Распределение Шарлье 8

6.Распределение Бернулли 9

7.Бета-распределение 10

8.Распределение Коши 11

9.Хи-квадрат распределение 12

10.Экспоненциальное распределение 13

11.Экстремальное значение 14

12.F распределение 15

13.Гамма-распределение 16

14.Геометрическое распределение 17

15.Распределение Гомперца 18

16.Распределение Лапласа 19

17.Логистическое распределение 20

18.Логнормальное распределение 21

19.Распределение Парето 22

20.Распределение Рэлея 23

21.Равномерное распределение 24

22.Распределение Стьюдента 25

23. Распределение Вейбулла 26

Список литературы: 27

1. Биноминальное распределение

Биномиальное распределение - одно из важнейших распределений вероятностей дискретно изменяющейся случайной величины. Биномиальным распределением называется распределение вероятностей числа m наступления события А в n взаимно независимых наблюдениях. Часто событие А называют "успехом" наблюдения, а противоположное ему событие - "неуспехом", но это обозначение весьма условное.

Условия биномиального распределения:

• 
  в общей сложности проведено n испытаний, в которых событие А может наступить или не наступить;
  
• 
  событие А в каждом из испытаний может наступить с одной и той же вероятностью p;
  
• 
  испытания являются взаимно независимыми. [4.]
  

Биномиальное распределение полезно для описания распределения биномиальных событий, таких как число мужчин и женщин в случайно выбранных компаниях или число дефектов в выборке продукции из 20 единиц. Биномиальное распределение имеет вид:



где
p - вероятность успеха в каждом испытании

q - величина, равная 1-p

n - число независимых испытаний. [1.]

2. Распределение Пуассона

Распределение Пуассона - случай биномиального распределения, когда число испытаний n достаточно большое, а вероятность p события A мала ( ).

Распределение Пуассона называют также распределением редких событий. Например, рождение за год трёх или четырёх близнецов, тот же закон распределения имеет число распавшихся в единицу времени атомов радиоактивного вещества и др. [4.]

Примеры переменных, распределенных по закону Пуассона, дают число несчастных случаев, число фатальных дефектов в производственном процессе. Распределение Пуассона определяется формулой: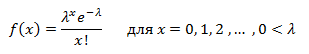



где
- ожидаемое значение x (среднее)
- число Эйлера (2.71...) [1.]

Закон Пуассона зависит от одного параметра - λ (лямбда), смысл которого в следующем: он является одновременно математическим ожиданием и дисперсией случаной величины, распределённой по закону Пуассона.

Во-первых, распределение Пуассона является предельным для биномиального распределения, когда число опытов n неограниченно увеличивается (стремится к бесконечности) и одновременно вероятность p успеха в одном опыте неограниченно уменьшается (стремится к нулю), но так, что их произведение np сохраняется в пределе постоянным и равным λ (лямбде):

.

В математическом анализе доказано, что распределение Пуассона с параметромλ = np можно приближенно применять вместо биномиального, когда число опытов nочень велико, а вероятность p очень мала, то есть в каждом отдельном опыте событие A появляется крайне редко.

Во-вторых, распределение Пуассона имеет место, когда есть поток событий, называемым простейшим (или стационарным пуассоновским потоком). Потоком событий называют последовательность таких моментов, как поступление вызовов на коммуникационный узел, приходы посетителей в магазин, прибытие составов на сортировочную горку и тому подобных. Пуассоновский поток обладает следующими свойствами:

• 
  стационарность: вероятность наступления m событий в определённый период времени постоянна и не зависит от начала отсчёта времени, а зависит только от длины участка времени;
  
• 
  ординарность: вероятность попадания на малый участок времени двух или более событий пренебрежимо мала по сравнению с вероятностью попадания на него одного события;
  
• 
  отсутствие последствия: вероятность наступления m событий в определённый период времени не зависит от того, сколько событий наступило в предыдущий период. [4.]
  

3. Нормальное распределение

Нормальное распределение (так называемая колоколообразная кривая, симметричная относительно среднего) - это теоретическая функция, особенно часто используемая в статистике (см. также Элементарные понятия статистики). Вообще, нормальное распределение дает хорошую модель, если:

1. Имеется сильная тенденция данных принимать центральное значение;

2. Положительные и отрицательные отклонения от этого центрального значения равновероятны;

3. Частота отклонений быстро падает, когда отклонения становятся большими.

Механизм, лежащий в основе нормального распределения, можно представить следующим образом. Имеется бесконечное число независимых случайных событий, которые вносят вклад в значения наблюдаемой переменной. Например, имеется практически бесконечное число факторов, определяющих вес человека (тысячи генов, предрасположенность, болезни и т.д.). Таким образом, можно ожидать нормальное распределение для веса в популяции всех людей. Плотность нормального распределения имеет вид:



где
- среднее
- стандартное отклонение
- число Эйлера (2.71...)
- число Пи (3.14...)

Стандартное нормальное распределение часто используется в проверке гипотез. [1.]

4. Распределение Максвелла

Распределение Ма́ксвелла — распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию. Распределение Максвелла также применимо для электронных процессов переноса и других явлений. Распределение Максвелла применимо к множеству свойств индивидуальных молекул в газе. О нём обычно думают как о распределении энергий молекул в газе, но оно может также применяться к распределению скоростей, импульсов, и модуля импульсов молекул. Также оно может быть выражено как дискретное распределение по множеству дискретных уровней энергии, или как непрерывное распределение по некоторому континууму энергии. [5.]



В этой формуле а = 0,6267 х - параметр распределения, определяемый через среднюю арифметическую х варьирующего признака; t=xi/a, где xi - числовые значения случайной величины Х; dх- разность между двумя смежннми значениями переменной величины Х.

Указанием на то, что эмпирическое распределение следует закону Максвелла, служит равенство между средним квадратическим отклонением и величиной 0,674 а, т. е. sx=0,674 а, тогда как для распределения Пуассона характерно равенство Sx^2 =Х.

Чтобы рассчитать по формуле теоретические частоты, нужно проделать следующее. 1. Определить среднюю арифметическую эмпирического вариационного ряда и параметр а. 2. Разделить каждую классовую варианту xi на величину а, что даст значения t. 3. Найти для каждого значения t=xi/a 4. Определить значения t^2/a. 5. Умножить значения t^2/a на удвоенную величину t и на величину классового промежутка, т. е. определить P= (t^2/а)2f(t)л. 6. Умножить значения P на общее число наблюдений n, получить теоретические (выравнивающие частоты данного вариационного ряда, т. е. f' =Рn. [3.]

5. Распределение Шарлье

В экономике редко встречаются симметричные распределения, чаще всего это ассиметричные распределения.

При выравнивании таких рядов важно найти кривую, которая бы учитывала ассиметрию и эксцессу ряда.

Для рядов с умеренной асимметрией такой кривой может служить распределение Шарлье, частоты которой рассчитываются по формуле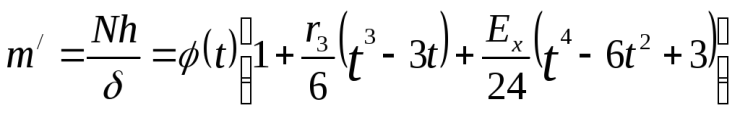



где N- общее число единиц совокупности

- нормированный момент третьего порядка, выступающий в качестве показателя асимметрии ряда

- показатель эксцесса

- нормированные отклонения, по которой определяется

при нормальном распределении, иE₃=0. подставим в формулу и получим т.о распределение Шарлье представляет собой как бы нормальное распределение, скорректированное на показатели ассиметрии и эксцесса. [2.]

6. Распределение Бернулли

Это распределение наилучшим образом описывает ситуации, где испытание имеет результат успех, либо неуспех, например, при бросании монеты, или при моделировании удачной или неудачной хирургической операции. Распределение Бернулли определяется формулой:



где p - вероятность того, что определенное событие (например, успех) произойдет. [1.]

7. Бета-распределение

Бета-распределение часто используется для описания процессов, обладающих естественными нижним и верхним пределами. Бета распределения определяется формулой: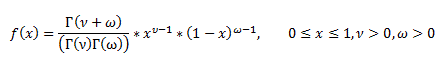



где
Г - гамма-функция
- параметры (формы) [1.]

8. Распределение Коши

Распределение Коши интересно по теоретическим причинам. Хотя среднее можно взять как ноль, так как распределение симметрично относительно нуля, математическое ожидание, дисперсия и моменты более высоких порядков не вычислены. Распределение Коши имеет вид: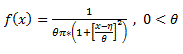



где
- параметр положения (медиана)
- число пи (3.1415...) [1.]

9. Хи-квадрат распределение

Распределение суммы квадратов независимых случайных переменных, каждая из которых имеет стандартное нормальное распределение имеет следующий вид:



где
v - число степеней свободы
e - число Эйлера (2.71...)
Г - гамма-функция [1.]

10. Экспоненциальное распределение

Экспоненциальный закон распределения называемый также основным законом надеж­ности, часто используют для прогнозирования надежности в период нормальной эксплуата­ции изделий, когда постепенные отказы еще не проявились и надежность характеризуется внезапными отказами. Эти отказы вызываются неблагоприятным стечением многих обстоя­тельств и поэтому имеют постоянную интенсивность. Экспоненциальное распределение на­ходит довольно широкое применение в теории массового обслуживания, описывает распре­деление наработки на отказ сложных изделий, время безотказной работы элементов радио­электронной аппаратуры. [2.]

Если T- время между наступлениями редких событий, происходящих в среднем с интенсивностью l то величина T имеет экспоненциальное распределение с параметром l (лямбда). Экспоненциальное распределение часто используется для описания интервалов времени между последовательными случайными событиями, например, интервалов времени между автомобилями, пересекающими перекресток, длительностей жизни электронных приборов или приходов покупателей в кассу бакалейного магазина. Плотность экспоненциального распределения имеет вид:



где
(лямбда) - параметр экспоненциальной функции (альтернативной параметризацией является параметр масштаба b=1/ )
- основание натуральных логарифмов (2.71...) [1.]

11. Экстремальное значение

Распределение экстремальных значений используется при моделировании экстремальных событий, например, уровней наводнений, скоростей вихрей, максимума индексов рынков ценных бумаг за данный год и т.д.; это распределение также используется в теории надежности, например, для описания времени отказа электрических схем. Распределение экстремальных значений (тип I) имеет плотность вида:



где
a - параметр положения
b - параметр масштаба
e - основание натуральных логарифмов (2.71...)

Это распределение иногда называют распределением наибольшего экстремального значения. [1.]

12. F распределение

F распределение в большинстве случаев используется в критериях дисперсии (например, ANOVA). Отношение двух хи-квадратов деленное на соответствующие степени свободы имеет F распределение. Ј x) имеет следующий вид (для n = 1, 2, ...; w = 1, 2, ...):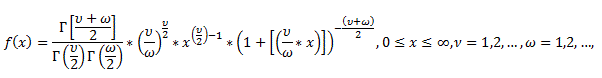



где
- степени свободы
Г - гамма - функция. [1.]

13. Гамма-распределение

Гамма-распределение является двухпараметрическим распределением. Оно занимает важное место в теории надежности. Плотность распределения имеет ограничение с одной стороны (0 ≤ х < ≤∞). Гамма-распределение широко применяют при описании появления отказов стареющих эле­ментов, времени восстановления, наработки на отказ резервированных систем. При различ­ных параметрах гамма-распределение принимает разнообразные формы, что и объясняет его широкое применение. [2.]

Плотность экспоненциального распределения имеет моду 0. Во многих примерах, заранее известно, что мода рассматриваемой случайной переменной не равна 0 (например, когда моделируется распределение длительности жизни электрических ламп или реальная (измеренная секундомером) длительность баскетбольного матча). В этих случаях Гамма распределение более подходит для описания распределения. Плотность Гамма распределения имеет вид:




Г - гамма-функция
b - параметр масштаба
c - параметр (формы)
e - число Эйлера (2.71...) [1.]

14. Геометрическое распределение

Если проводятся независимые испытания Бернулли и подсчитывается количество испытаний до наступления успеха, то это число имеет геометрическое распределение. Геометрическое распределение определяется формулой:



где
p - вероятность наступления определенного события (например, успеха). [1.]

15. Распределение Гомперца

Это распределение является теоретическим распределением времен отказов или времени жизни. Гомперц (1825) предложил вероятностную модель человеческой смертности, основывающаяся на предположениях, что среднее истощение человеческой силы должно быть таким, чтобы к концу каждого бесконечно малого интервала времени он теряет равную порцию оставшейся энергии. Это с целью избежания смерти по отношению к разрушению, которое наблюдалось в начале этого интервала. Распределение Гомперца имеет вид:



оно часто используется в Анализе Выживаемости. [1.]

16. Распределение Лапласа

Лапласа (или двойное экспоненциальное) распределение имеет функцию плотности распределения: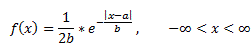



где
a - среднее распределения
b - параметр масштаба
e - число Эйлера (2.71...) [1.]

17. Логистическое распределение

Логистическое распределение используется в модели двоичного отклика (например, Пол) и обычно используется в логит регрессии. Плотность логистического распределения имеет вид: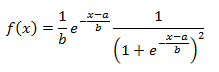



где

a - среднее распределения
b - параметр масштаба
e - число Эйлера (2.71...) [1.]

18. Логнормальное распределение

Логнормальное распределение часто используется в моделировании таких переменных, как персональные доходы, возраст новобрачных (точнее, первый раз вступающих в брак) или допустимое отклонение от стандарта вредных веществ в продуктах питания. В общем, если величина x имеет нормальное распределение, то y = e x имеет логнормальное распределение. Плотность логнормального распределения имеет вид: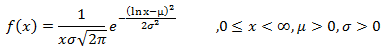



где
- параметр масштаба
- параметр (формы)
- число Эйлера (2.71...) [1.]

19. Распределение Парето

Распределение Парето обычно используется для производственных процессов. Например, машина, которая производит медную проволоку может иногда делать небольшие трещинки в нескольких точках на протяжении всей длине проволоки. Распределение Парето можно использовать в модели длины проволоки между последовательными трещинами. Плотность распределения Парето имеет вид:



где
c - параметр (формы) распределения. [1.]

20. Распределение Рэлея

Если две переменные y1 and y2 являются независимыми друг от друга и нормально распределены с одинаковой дисперсией, то переменная 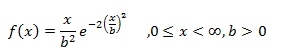будет иметь распределение Релея. Примером такой случайной величины будет расстояние дротиков от центра мишени при бросании дротиков, если отклонения от центра мишени по горизонтали и вертикали имеют нормальное распределение с одинаковой дисперсией. Распределение Релея имеет плотность:



где
b - параметр масштаба
e - число Эйлера (2.71...) [1.]

21. Равномерное распределение

Равномерное распределение полезно для описания переменных, у которых значения плотности одинаковы на отрезке a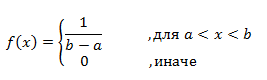


где a - константы. [1.]

22. Распределение Стьюдента

Распределение Стьюдента симметрично относительно нуля и его главная форма схожа со стандартным нормальным распределением. Обычно это распределение используется в проверке гипотез о среднем различных популяций. Распределение Стьюдента выглядит следующим образом (для n = 1, 2, . . .):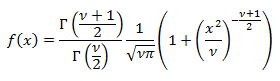



где
- число степеней свободы
- гамма-функция
- число Пи (3.1415...) [1.]

23. Распределение Вейбулла

Закон Вейбулла представляет собой двухпараметрическое распределение. Этот закон является универсальным, так как при соответствующих значениях параметров превраща­ется в нормальное, экспоненциальное и другие виды распределений. [2.]

Как описывалось выше, экспоненциальное распределение часто используется как модель, оценивающая время наработки до отказа в предположении, что вероятность отказа постоянна. Если вероятность отказа меняется с течением времени, используется распределение Вейбулла. Это распределение часто применяется при испытаниях на надежность, например, электрических реле, подшипников и т.п. Распределение Вейбулла имеет плотность вида: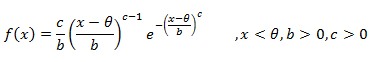



где
- параметр масштаба распределения
- параметр (формы) распределения
- параметр положения распределения
- число Эйлера (2.71...) [1.]

Список литературы:

1. 
   http://statistica.ru
   
2. 
   https://studopedia.org/
   
3. 
   Лакин, Г.Ф. Биометрия / Г.Ф. Лакин. - М.: Высшая школа; Издание 3-е, перераб. и доп., 1980. - 293 c.
   
4. 
   https://function-x.ru/probabilities_distribution_binomial.html
   
5. 
   https://ru.wikipedia.org/wiki/Распределение_Максвелла