Математика. Реферат по математике. Реферат по дисциплине Математика Математическая статистика и её роль в медицине и здравоохранении

• Название: Реферат по дисциплине Математика Математическая статистика и её роль в медицине и здравоохранении
• Анкор: Математика
• Дата: 25.12.2022
• Размер: 47.27 Kb.
• Имя файла: Реферат по математике.docx
• Тип: Реферат; #863376

Департамент охраны здоровья населения Кемеровской области

Новокузнецкий филиал

Государственного бюджетного образовательного учреждения

среднего профессионального образования

«Кемеровский областной медицинский колледж»

Реферат

по дисциплине: « Математика»

Математическая статистика и её роль в медицине и здравоохранении.

Выполнила: студентка ФШ-202 группы,
специальности 31.02.01 Лечебное дело
Черновол Анна Сергеевна
Проверила: Шилепина Надежда Ивановна

Содержани

ВВЕДЕНИЕ 3

1. 
   ВВЕДЕНИЕ 3
   
2. 
   ЧТО ТАКОЕ МАТЕМАТИЧЕСКАЯ СТАТИСТИКА? 3
   
3. 
   ИСТОРИЯ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ 5
   
4. 
   РОЛЬ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ В МЕДИЦИНЕ 6
   
5. 
   РАСЧЕТНЫЕ ПОКАЗАТЕЛИ 8
   
6. 
   ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ 9
   
7. 
   ХРАКТЕРИСТИКА РАССЕЯННОГО ВОКРУГ СВОЕГО СРЕДНЕГО 12
   
8. 
   ЗАКЛЮЧЕНИЕ 13
   
9. 
   СПИСОК ЛИТЕРАТУРЫ 14
   

ВВЕДЕНИЕ

ЧТО ТАКОЕ МАТЕМАТИЧЕСКАЯ СТАТИСТИКА?

Математическая статистика — это наука, разрабатывающая математические методы систематизации и использования статистических данных для научных и практических выводов.

Статистика самостоятельная общественная наука, изучающая количественную сторону массовых общественных явлений в неразрывной связи с их качественной стороной.

Во многих своих разделах математическая статистика опирается на теорию вероятностей, позволяющую оценить надёжность и точность выводов, делаемых на основании ограниченного статистического материала (напр., оценить необходимый объём выборки для получения результатов требуемой точности при выборочном обследовании). 

Математическая статистика - раздел математики, разрабатывающий методы регистрации, описания и анализа данных наблюдений и экспериментов с целью построения вероятностных моделей массовых случайных явлений. В зависимости от математической природы конкретных результатов наблюдений статистика математическая делится на статистику чисел, многомерный статистический анализ, анализ функций (процессов) и временных рядов, статистику объектов нечисловой природы.

Медицинская статистика делится на разделы: 

1)общетеоретические и методические основы статистики 
2)статистика здоровья населения; 
3) статистика здравоохранения. 

История науки позволяет выделить следующие этапы развития, обусловленные доминирующей методологией и уровнем познания предмета исследования: 

1)эмпирический этап, характеризующийся накоплением и описанием фактов, частичной их систематизацией; 

2)теоретический этап — анализ и синтез накопленных фактов в виде отдельных концепций, объединяющихся в относительно непротиворечивые теории; 

3)количественный, математический этап — на базе накопленных фактов исследуются количественные закономерности, создаются математические модели исследуемых явлений и объектов.

ИСТОРИЯ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

Математическая статистика как наука начинается с работ знаменитого немецкого математика Карла Фридриха Гаусса (1777-1855), который на основе теории вероятностей исследовал и обосновал метод наименьших квадратов, созданный им в 1795 г. и примененный для обработки астрономических данных (с целью уточнения орбиты малой планеты Церера). Его именем часто называют одно из наиболее популярных распределений вероятностей – нормальное, а в теории случайных процессов основной объект изучения – гауссовские процессы. В конце XIX в. – начале ХХ в. крупный вклад в математическую статистику внесли английские исследователи, прежде всего К.Пирсон (1857-1936) и Р.А.Фишер (1890-1962). В частности, Пирсон разработал критерий «хи-квадрат» проверки статистических гипотез, а Фишер – дисперсионный анализ, теорию планирования эксперимента, метод максимального правдоподобия оценки параметров. В 30-е годы ХХ в. поляк Ежи Нейман (1894-1977) и англичанин Э.Пирсон развили общую теорию проверки статистических гипотез, а советские математики академик А.Н. Колмогоров (1903-1987) и член-корреспондент АН СССР Н.В.Смирнов (1900-1966) заложили основы непараметрической статистики. В сороковые годы ХХ в. румын А. Вальд (1902-1950) построил теорию последовательного статистического анализа.

РОЛЬ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ В МЕДИЦИНЕ

Вначале статистика применялась в основном в области социально-экономических наук и демографии, а это неизбежно заставляло исследователей более глубоко заниматься вопросами медицины. 

Основателем теории статистики считается бельгийский статистик Адольф Кетле (1796-1874). Он приводит примеры использования статистических наблюдений в медицине: Два профессора сделали любопытное наблюдение относительно скорости пульса. Сравнив мои наблюдения с их данными, они заметили, что между ростом и числом пульса существует зависимость. Возраст может влиять на пульс только при изменении роста, который играет в этом случае роль регулирующего элемента. Число ударов пульса находится, таким образом, в обратном отношении с квадратным корнем роста. Приняв за рост среднего человека 1,684 м, они полагают число ударов пульса равным 70. Имея эти данные, можно вычислить число ударов пульса у человека какого бы то ни было роста. 

Самым активным сторонником использования статистики был основоположник военно-полевой хирургии Н. И. Пирогов. Еще в 1849г., говоря об успехах отечественной хирургии, он указывал: Приложение статистики для определения диагностической важности симптомов и достоинства операций можно рассматривать как важное приобретение новейшей хирургии. 

В 60-е годы XX века, после очевидных успехов прикладной статистики в технике и точных науках, вновь начал расти интерес к использованию статистики в медицине. В.В. Алпатов в статье О роли математики в медицине писал: Чрезвычайно важна математическая оценка терапевтических воздействий на человека. Новые лечебные мероприятия имеют право заменить собою мероприятия, уже вошедшие в практику, лишь после обоснованных статистических испытаний сравнительного характера. ... Огромное применение может получить статистическая теория в постановке клинических и неклинических испытаний новых терапевтических и хирургических мероприятий. 

Прошли те времена, когда применение статистических методов в медицине ставилось под сомнение. Статистические подходы лежат в основе современного научного поиска, без которого познание во многих областях науки и техники невозможно. Невозможно оно и в области медицины. 

Медицинская статистика должна быть нацелена на решение наиболее выраженных современных проблем в здоровье населения. Основными проблемами здесь, как известно, являются необходимость снижения заболеваемости, смертности и увеличения продолжительности жизни населения. Соответственно, на данном этапе основная информация должна быть подчинена решению этой задачи. Должны подробно проводиться данные, характеризующие с разных сторон ведущие причины смерти, заболеваемости, частоту и характер контактов больных с медицинскими учреждениями, обеспечение нуждающихся необходимыми видами лечения, включая высокотехнологичные.

РАСЧЕТНЫЕ ПОКАЗАТЕЛИ

Одним из важных направлений медицинской статистики служит разработка научно обоснованных критериев (показателей) состояния здоровья населения и деятельности учреждений и органов здравоохранения, а также систем таких критериев (показателей), которые могут быть использованы в процессе управленческой работы с целью объективной оценки складывающихся конкретных ситуаций (врачебной деятельности, деятельности конкретных учреждений, их групп и т.д.), их планирования и прогнозирования. 

Важными медико-статистическими показателями являются показатели здоровья населения (смертность, заболеваемость и др.), показатели, характеризующие работу лечебно-профилактических учреждений (городской поликлиники, детской поликлиники, женской консультации, стоматологической поликлиники, больницы, родильного дома, скорой медицинской помощи и др.), санитарно-профилактических, аптечных и других медицинских учреждений (подразделений). 

Медико-статистические показатели периодически пересматриваются в соответствии с новыми задачами здравоохранения, развитием медицинской науки и практики, технической оснащенности служб здравоохранения. 

Для наглядности результаты исследования могут быть представлены в виде различных графических изображений: 
1. Диаграммы

а) линейные

б) плоскостная(прямоугольная, секторная, полярная)

в) фигурная

2. Картография и кардиограмма

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

В математической статистике принято выделять два основных направления исследований:

1. Оценка параметров генеральной совокупности.

2. Проверка статистических гипотез (некоторых априорных предположений).

Основными понятиями математической статистики являются: генеральная совокупность, выборка, теоретическая функция распределения.

Генеральной совокупностью является набор всех мыслимых статистических данных при наблюдениях случайной величины.

Х_Г = {х₁, х₂, х₃, …, х_N, } = { х_i ; i=1,N }

Наблюдаемая случайная величина Х называется признаком или фактором выборки. Генеральная совокупность – есть статистический аналог случайной величины, ее объем N обычно велик, поэтому из нее выбирается часть данных, называемая выборочной совокупностью или просто выборкой.

Х_В = {х₁, х₂, х₃, …, х_n, } = { х_i ; i=1,n }

Х_В Ì Х_Г, n £ N

Выборка – это совокупность случайно отобранных наблюдений (объектов) из генеральной совокупности для непосредственного изучения. Количество объектов в выборке называется объемом выборки и обозначается n. Обычно выборка составляет 5%-10% от генеральной совокупности. Использование выборки для построения закономерностей, которым подчинена наблюдаемая случайная величина, позволяет избежать ее сплошного (массового) наблюдения, что часто бывает ресурсоемким процессом, а то и просто невозможным.

Например, популяция представляет собой множество индивидуумов. Изучение целой популяции трудоемко и дорого, поэтому собирают данные по выборке индивидуумов, которых считают представителями этой популяции, позволяющими сделать вывод относительно этой популяции.

Однако, выборка обязательно должна удовлетворять условию репрезентативности, т.е. давать обоснованное представление о генеральной совокупности. Как сформировать репрезентативную (представительную) выборку? В идеале стремятся получить случайную (рандомизированную) выборку. Для этого составляют список всех индивидуумов в популяции и случайно их отбирают. Но иной раз затраты при составлении списка могут оказаться недопустимыми и тогда берут приемлемую выборку, например, одну клинику, больницу и исследуют всех пациентов в этой клинике с данным заболеванием.

Каждый элемент выборки   называется вариантой. Число повторений варианты   в выборке называется частотой встречаемости   . Величина   называется относительной частотой варианты, т.е. находится как отношение абсолютной частоты варианты   ко всему объему выборки. Последовательность вариант, записанных в возрастающем порядке, называется вариационным рядом.

Рассмотрим три формы вариационного ряда: ранжированный, дискретный и интервальный.

Ранжированный ряд - это перечень отдельных единиц совокупности в порядке возрастания изучаемого признака.

Дискретный вариационный ряд представляет собой таблицу, состоящую из граф, либо строк: конкретного значения признака х_i и абсолютной частоты n_i (или относительной частоты ω_i) проявления i-го значения признака x.

Статистическое распределение – это совокупность вариант 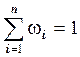  и соответствующих им частот   . Для проверки правильности записи статистического распределения используют условие нормировки:   .

Интервальный вариационный ряд используется при большом числе наблюдений. Для построения такого ряда надо выбрать число интервалов признака и установить длину интервала. При большом числе групп величина интервала будет минимальна. Число групп в вариационном ряду можно найти по формуле Стерджеса:   (k-число групп, n - объем выборки), а ширину интервала – 

где   - максимальное;   - минимальное значения вариант, а их разность R носит название размаха вариации.

Исследуется выборка из 100 человек из совокупности всех студентов медицинского ВУЗа.

Решение: Рассчитаем число групп:   . Таким образом, для составления интервального ряда данную выборку лучше разбить на 7 или 8 групп. Совокупность групп, на которые разбиваются результаты наблюдений и частот получения результатов наблюдений в каждой группе, называют статистической совокупностью.

Для наглядного представления статистического распределения пользуются гистограммой.

Гистограмма частот – это ступенчатая фигура, состоящая из смежных прямоугольников, построенных на одной прямой, основания которых одинаковы и равны ширине интервала, а высота равна или частоте попадания в интервал   или относительной частоте ω_i.

ХРАКТЕРИСТИКА РАССЕЯННОГО ВОКРУГ СВОЕГО СРЕДНЕГО

Выборочная дисперсия – среднее арифметическое квадратов отклонения вариант от их среднего значения:

 Исправленная дисперсия при малых выборках n<30 

Среднее квадратическое отклонение – это квадратный корень из выборочной дисперсии:

 – исправленное значение (n<30). 

Коэффициент вариации СV – это отношение среднего квадратического отклонения к средней величине признака, выраженное в процентах:



Коэффициент вариации – это мера относительной изменчивости случайной величины, которая позволяет сравнивать разнородные величины, например, частоту сердечных сокращений (ЧСС, уд/мин), артериальное давление (АД, мм. рт. ст.) и температуру (   ) в единых единицах - процентах.

ЗАКЛЮЧЕНИЕ

Прошли те времена, когда применение статистических методов в медицине и биологии ставилось под сомнение. Статистические подходы лежат в основе современного научного поиска, без которого познание во многих областях науки и техники невозможно. Невозможно оно и в области медицины. Медицинская статистика должна быть нацелена на решение наиболее выраженных современных проблем в здоровье населения. Основными проблемами здесь, как известно, являются необходимость снижения заболеваемости, смертности и увеличения продолжительности жизни населения. Соответственно, на данном этапе основная информация должна быть подчинена решению этой задачи. Должны подробно приводиться данные, характеризующие с разных сторон ведущие причины смерти, заболеваемость, частоту и характер контактов больных с медицинскими учреждениями, обеспечение нуждающихся необходимыми видами лечения, включая высокотехнологичные.

И в общем, в настоящее время от работника, занятого в любой области науки, техники, производства, бизнеса и прочее, связанной с изучением массовых явлений, требуется, чтобы он был, по крайней мере, статистически грамотным человеком. В конечном счете, невозможно успешно специализироваться по многим дисциплинам без усвоения какого-либо статистического курса. Поэтому изучение математической статистики имеет большое значение.

Таким образом, математическая статистика и в медицине, и в здравоохранении играет очень важную роль.

Статистика в здравоохранении используется для: 

1. Развитие углубленных медико-биологических, физических и др. методов исследования, внедрение новой диагностической техники приводит к накоплению числовых данных, характеризующих состояние организма и окружающей среды. Принимая во внимание объем информации об организме можно понять необходимость синтеза данных с использованием статистических методов; 

2. Определение норм санитарно-гигиенического характера, расчета доз лекарственных препаратов, определение стандартов физического развития, оценки эффективности применяемых методов профилактики и лечения.

СПИСОК ЛИТЕРАТУРЫ

1.Гилярова М.Г., Математика для медицинских колледжей : [Текст]/ Гилярова М.Г. – Изд. 5-е. – Ростов н/Д : Феникс, 2016. – 442 с.

2.Филимонова Е.В. Математика: Учебное пособие для средних специальных учебных заведений.[Текст] / Е.В. Филимонова. Ростов н/Д.: Феникс, 2008.

3. Михеев В.С., Стяжкина О.В., Шведова О.М. Математика: Учебное пособие для среднего профессионального образования.[Электронный ресурс] / В.С.Михеев. Ростов н/Д.: Феникс, 2009. (дата обращения: 1.11.2019).

Новокузнецк,2019