Обработка экспериментальных данных (задачи). 8-47 3 метода. Реферат по дисциплине Обработка экспериментальных данных
 Скачать 68.92 Kb. Скачать 68.92 Kb.
|
|
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Казанский национальный исследовательский технологический университет» (ФГБОУ ВО «КНИТУ») Кафедра «Машины и аппараты химических производств» Направление (специальность) 15.03.02 – Технологические машины и оборудование Группа РЕФЕРАТ по дисциплине «Обработка экспериментальных данных» Исполнитель _______________________________ Руководитель ______________________________ Казань 2020 Задача 1. Экспериментально установлены зависимости плотности жидкого вещества вещества (метиловый спирт 100%) ρ, кг/м3 от температуры t, 10–100 ˚С. Определить коэффициенты регрессии а0 и а1 по выборке объемом n =10 методом выбранных точек, используя экспериментальные данные, приведенные в таблице 1. Рассчитать абсолютную и относительную погрешности полученного уравнения линейной регрессии. Для оценки линейной связи уравнения регрессии вычислить выборочный коэффициент корреляции. Таблица 1
Строим график по табличным значениям. Проводим прямую линию как можно ближе к нанесенным на график точкам (рис.1).  Рисунок 1 На этой прямой линии выбираем произвольные точки  и и  Пусть  = 25, тогда = 25, тогда 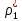 =787,9 =787,9Пусть 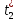 = 75, тогда = 75, тогда  = 811,9 = 811,9Составим систему уравнений   Решая эту систему, получаем:  Полученное уравнение регрессии  Выборочная средняя:     Выборочная дисперсии: 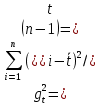 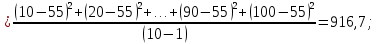   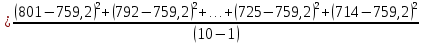   Выборочный коэффициент корреляции:  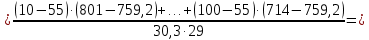  Расчет абсолютной и относительной погрешности. Таблица 2
Вывод: в рамках данной задачи я определил коэффициенты регрессии методом выбранных точек по экспериментальным данным. Рассчитал абсолютную и относительную погрешности полученного уравнения линейной регрессии и определил выборочный коэффициент корреляции 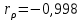 . .Задача 2. Экспериментально установлены зависимости плотности жидкого вещества вещества (метиловый спирт 100%) ρ, кг/м3 от температуры t, 10–100 ˚С. Определить коэффициенты регрессии а0 и а1 по выборке объемом n =10 методом средних, используя экспериментальные данные, приведенные в таблице 1. Рассчитать абсолютную и относительную погрешности полученного уравнения линейной регрессии. Для оценки линейной связи уравнения регрессии вычислить выборочный коэффициент корреляции. Определение коэффициентов регрессии. Разобъем суммы на две такие совокупности, для которых суммы 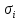 примерно одинаковы. примерно одинаковы.Таблица 3
Составим систему уравнений   Решая эту систему, получаем:  Уравнение регрессии 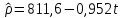 Выборочная средняя:     Выборочная дисперсии: 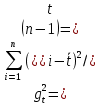 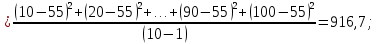   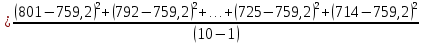   Выборочный коэффициент корреляции:  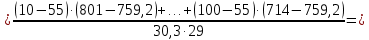  Расчет абсолютной и относительной погрешности Таблица 4
Вывод: в рамках данной задачи я определил коэффициенты регрессии методом средних по экспериментальным данным. Рассчитал абсолютную и относительную погрешности полученного уравнения линейной регрессии и определил выборочный коэффициент корреляции 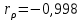 . .Задача 3. Экспериментально установлены зависимости плотности жидкого вещества вещества (метиловый спирт 100%) ρ, кг/м3 от температуры t, 10–100 ˚С. Определить коэффициенты регрессии а0 и а1 по выборке объемом n = 10 методом наименьших квадратов, используя экспериментальные данные, приведенные в таблице 1. Рассчитать абсолютную и относительную погрешности полученного уравнения линейной регрессии. Для оценки линейной связи уравнения регрессии вычислить выборочный коэффициент корреляции. Определение коэффициентов регрессии. Для решения систему уравнений составим вспомогательную таблицу Таблица 5
Составим систему уравнений   Решая эту систему, получаем:  Уравнение регрессии  Выборочная средняя:     Выборочная дисперсии: 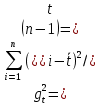 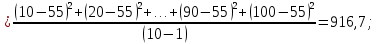   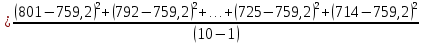   Выборочный коэффициент корреляции:  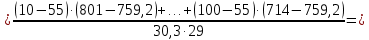  Расчет абсолютной и относительной погрешности Таблица 6
Вывод: в рамках данной задачи я определил коэффициенты регрессии методом наименьших квадратов по экспериментальным данным. Рассчитал абсолютную и относительную погрешности полученного уравнения линейной регрессии и определил выборочный коэффициент корреляции 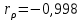 . . |

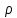



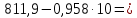 802,3
802,3 792,7
792,7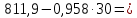 783,1
783,1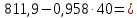 773,6
773,6 764
764 754,4
754,4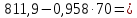 744,8
744,8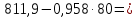 735,3
735,3 725,7
725,7 716,1
716,1

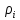

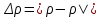
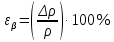
 802,1
802,1 792,6
792,6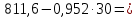 783
783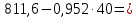 773,5
773,5 764
764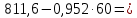 754,5
754,5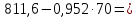 745
745 735,4
735,4 725,9
725,9 716,4
716,4