теория бойля мариотта. Минигулов ГРз1801 реферат. Реферат по дисциплине Подземная гидрогазодинамика по теме Линеаризация уравнения Лейбензона. Сведение задачи нестационарной фильтрации газа к задаче фильтрации упругой жидкости
 Скачать 28.62 Kb. Скачать 28.62 Kb.
|
|
Министерство науки и высшего образования Российской Федерации ФГБОУ ВО Уфимский государственный нефтяной технический университет Кафедра Разработка и эксплуатация нефтяных и газонефтяных месторождений РЕФЕРАТ по дисциплине «Подземная гидрогазодинамика» по теме: Линеаризация уравнения Лейбензона. Сведение задачи нестационарной фильтрации газа к задаче фильтрации упругой жидкости. Выполнил: студент ГРз-18-01 Минигулов А.С. Проверил: преподаватель Яркеева Н.Р. Уфа 2022 Если заменить нелинейное дифференциальное уравнение  ; ; ; (15.1) ; (15.1)линейным, т.е. линеаризовать его, то оно упростится – для линейного уравнения существуют точные аналитические решения. Ясно, что эти точные решения линеаризованного уравнения будут приближенными для нелинейного. Оценить погрешность решения, которая возникает при замене точного уравнения линеаризованным, можно, например, сравнивая приближенное решение с решением на ЭВМ точного уравнения. Были предложены различные способы линеаризации уравнения (15.1). Если рассматривается плоскорадиальный приток к скважине, то из теории установившейся фильтрации газа, воронка депрессии очень крутая, и в большей части пласта давление мало отличается от контурного. На этом основании Лейбензон предложил заменить переменное давление р в коэффициенте уравнения (15.1) на постоянное давление pk равное начальному давлению в пласте. Тогда, обозначив ā=  , получим вместо уравнения (15.1) уравнение , получим вместо уравнения (15.1) уравнение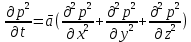 ; (15.2) ; (15.2)которое является линейным уравнением пьезопроводности относительно функции р2 где ā - константа, аналогичная коэффициенту пьезопроводности. Такой способ линеаризации, когда переменный коэффициент и в уравнении (15.2) при различных значениях давления принимается константой, называется линеаризацией по Лейбензону. Используем линеаризованное уравнение (15.2) для решения конкретной задачи о притоке газа в скважину бесконечно малого радиуса (точечный сток), расположенную в пласте бесконечной протяженности с постоянной толщиной h. В начальный момент времени пласт невозмущен, т. е. давление во всем пласте постоянно и равно р2. С этого момента начинается отбор газа с постоянным дебитом Qат. Нужно найти изменение давления по пласту с течением времени p(r,t). Для плоскорадиальной фильтрации газа (15.2) запишется следующим образом  ; (15.3) ; (15.3)Здесь выражение 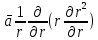 представляет собой оператор Лапласа представляет собой оператор Лапласав полярных координатах относительно квадрата давления для плоско-радиального движения. Уравнение (15.3) надо проинтегрировать при начальном условии p2=p2k при t=0, 0<r<∞ . (15.4) и при граничном условии в удаленных точках p2=p2k при t>0, r=∞ . (15.5) Выведем условие для давления на забое скважины. Для этого запишем выражение для массового дебита исходя из закона Дарси в дифференциальной форме для плоскорадиальной фильтрации:  Использовав равенства Qm=pamQamи 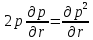 и сократив на pam , получим:   Из этого соотношения выразим условие на стенке газовой скважины бесконечно малого радиуса:  при r=0 при r=0Решением поставленной задачи для упругой жидкости является основная формула упругого режима :  (15.6) (15.6)Аналогия между фильтрацией упругой жидкости и газа свидетельствует о том, что, заменив в формуле (15.6) давление на р2, a на ā , Qƞ/2πkh - на Qampamƞ/(πkh) получим решение поставленной задачи для, газа 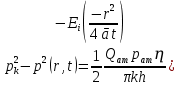 ; (15.7) ; (15.7)или 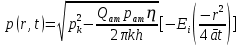 ; (15.8) ; (15.8)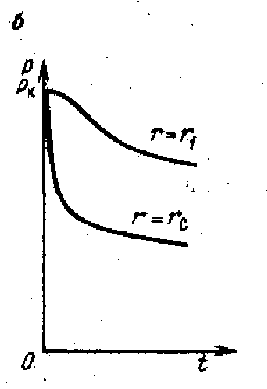 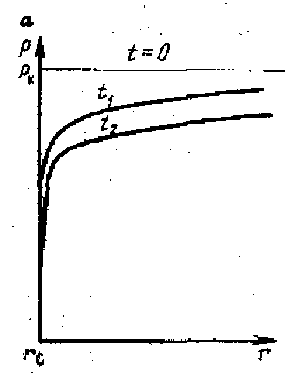
Это и есть основное решение линеаризованного уравнения Лейбензона. |
