Реферат диф исчисления. Реферат по теме История дифференциального исчисления
 Скачать 114.09 Kb.
|
|
Государственное автономное профессиональное образование учреждение «Оренбургский областной медицинский колледж» Реферат по теме: «История дифференциального исчисления» Выполнила студентка 1 курса Ф-101у группы Абоимова Александра Проверил руководитель: Кононова Марина Владимировна 2022 год Содержание:
ВведениеЦель работы: «Изучение основных понятий дифференциального расчета и знакомство с историческими фактами. Исследования по дифференциальным исчислениям проводились многими известными учеными, Ньютоном, Лейбницам, Барроу и другими. Впрочем, главной заслуга - Готфрид Вильгельм Лейбниц. Ученый устанавливал четкие правила для простых операций, которые строят сложнее, а также постоянно связывают их с определённой системой символов. Это стало преимуществом математикам, которые чувствовали предмет более глубоко. Это обстоятельство стало причиной создания Лейбницской школы.  История применения дифференцированного исчисленияДифференциальные исчисления были созданы Ньютоном и Лейбницем в конце 17 века, основанные на двух задачах: 1) разыскания касательных к произвольной линейке; 2) разыскания скорости при произвольном законе движения. Еще ранее понятие производного встречалось в трудах итальянской математики Тартальи в 1500-1557 годах – здесь возникла касательная в изучении вопроса о наклоне орудия с наибольшей дальностью полета снаряда. В математике производная является числовым выражением степени перемещения величины, находящейся в одном и том же месте под воздействием различных условий. Формула производного часто применяется в работах ведущих математиков XVIII столетия. Ее использовали Ньютон, Лейбниц и Ньютон. Он посвятил ей целый труд по математике известного ученого Галилея Галилея. Затем производные и разные изложения, применяемые ими, стали встречаться в работах декарта, французской математики Роберваль и англичан Грегора. Больший вклад в изучение производных внесли умы, такие как Лопитал, Бернулл, Лагранжа. Дифференциальные исчисления являются широко применимыми математическими аппаратами для анализа экономических показателей. Базовая задача анализа экономической величины - изучение экономических связей, записанных как функции. Каким образом государство изменит доход при увеличении налоговых налогов или ввести импортные пошлины. Выручка компании будет увеличиваться или уменьшаться при росте цен на ее продукты. В каких пропорциях дополнительное оборудование способно заменить выбранных сотрудников. Чтобы решить такие задачи, нужно построить функции соединения, входящие в нее переменные, которые потом изучаются методами дифференциального расчета. Очень часто в экономике нужно найти наилучший или оптимальный показатель: наивысшая производительность, наибольшая прибыль, наибольший выпуск, минимальная издержка и так далее. Каждый показатель является функцией одной или несколькими аргументами. Поэтому нахождение оптимальных значений, показателей сводится к тому, чтобы найти экстремальную функцию. При использовании производной можно увидеть планируемые действия и понять необходимость их, а также помогать экономистам составить успешные бизнес-планы. Производная является основным понятием дифференциального расчета, которое характеризует скорость изменений функции в этой точке. Определяется в качестве предела отношения приравнивания функции к пределу приравнивания аргумента при желании приравнивания аргумента к минимуму, если существует такой предел. Функция с конечным производным в определенной точке называется дифференцированной. Процесс расчета производной - дифференцированный процесс. Второй процесс - интеграция. Впрочем, в настоящее время, благодаря научно-техническому прогрессу, в том числе быстрой эволюции вычислительной системы, дифференциальная арифметика становится все более актуальной в решении и простых, и сверх простых проблем. Лейбниц и дифференциальное исчислениеЛ  ейбниц родился в Лейпциге. В 1661 году поступил на юридический факультет в Лейпцигском университете. Кроме юридических наук изучал физику, математику, изучал химию, геологию, конструировал ветряный двигатель для выкачивания воды из шахты.Особо плодотворным было научное сотрудничество Лейбницы по математике. Большое влияние на изучение математики Лейбнице оказало Гюйгенс. Последний предлагал задачу определить сумму треугольных чисел, то есть чисел вида.  .Но Лейбниц и не остановился на решении данной задачи, он также нашел число, обратное к пирамидам и другие ряды, что было подготовкой для создания дифференциальных исчислений. Лейбница продолжила работу в данном направлении, изучая работы Кавальеры, Григория, Паскаля по инфинизимальным исследованиям. Ученый научился применять свои работы в данной области так, что мог самостоятельно их использовать, что доказывает новый инфинизимальный преобразований, из которых получилось большинство известной квадратуры в этот период. Теперь это изменение происходит из выражения площади секторов, ограниченных двумя векторами радиуса и безграничной дугой. Это преобразование получается из выражения площади секторов, ограниченных двумя радиусными векторами. Само Лейбниц, создавая дифференциальное исчисление, также использовал это дифференциальное выражение. В ранних письмах и рукописях он применяет ту же геометрию, которую давали его предки. На рисунке. 1 к кривой A 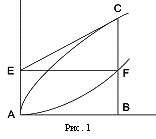 C проведен касательный EC, который отсекает отрезок АЭ. Это отрезок принимается как ордината BF-точки F, у которой одинаковая абсцисса точки C.Сектор, ограниченный геометрическим положением данной точки, оси абсцисса и двух ординат, больше, чем сектор, ограниченный дугой кривой AC, и радиусом-вектором, проведенным из А в ее концы, в 2 раза. Если рассмотреть бесконечно малые части этих фигур (прямоугольники и треугольники) то, из подобия треугольников можно увидеть, что основание и высота бесконечно малого прямоугольника обратно пропорциональны высоте и основанию соответствующего бесконечно малого треугольника. Изучение бесконечного знакопеременного ряда привела ученого к тому, что он рассматривает сходимость таких ряда. Лейбниц утверждал, что бесконечное число с чередованием знаков имеет конечное число, если абсолютное число членов уменьшается и идет в пределах нуля. Несмотря на изучение рядов, Лейбница выдвинула ряд мыслей о том, что касается произвольной кривы, используя характерный треугольник, образованный различиями между абсциссами и ординатами двумя бесконечно близкими точками и лежит между этими точки дугой. Эти величины позже будут названы ученым dх,dу,dz. Но похожие размышления были обнаружены Лейбницем у Барроу и Грегори после изучения их работ. Однако исследователем были сделаны интересные наблюдения. Вследствие того, что при рассматриваемом определении касательных применяются разности dу между ординатами, которые соответствуют разностям между абсциссами dх, то в обратную сторону ордината у является суммой этих разностей. На основании того, что задача о квадратуре сводится к определению такой же суммы, Лейбниц высказывает мнение, что почти все учение об обратных задачах на касательные можно представить в виде квадратур. Таким образом, была установлена связь между дифференцированием и интегрированием. Предположив, что основание треугольника ACD (бесконечно малого сектора) элемент дуги кривой CD, тогда высотой будет перпендикуляр AH, выходящий из начала координат на касательную DCH. Прямоугольные треугольники AHE и CDG подобны, следовательно,  . Что в силу равенств  и  можно записать как: .Последнее равенство показывает, что площадь прямоугольника равна удвоенной площади сектора:  .Используя метод Ферма для определения касательных к параболам и гиперболам разных порядков, Лейбниц определил, что вспомогательная кривая также является параболой и гиперболой того же порядка, но с новым параметром. Таким образом, вычисляя площадь круга, ученый получил  и разложил ее в ряд. Он нашел аналогичный ряд для  .Таким образом, была установлена связь между дифференцированием и интегрированием. В процессе работы над этими исследованиями ученый развил свою инфинитезимальную символику. Исследования также проводились по определенным установленным им правилам исчисления. Эти правила используются и теперь. Исаак Ньютон и дифференциальное исчисление В  1665 году. Исаак Ньютон окончил университет Кембриджа и планировал начать работать там же в родном колледже Тринити.Впрочем, чума, бушующая в Англии заставила Ньютон уединиться в своей фермерской ферме в Вулстоне. «Чумные отпуска» прошли почти на 2 года.«В то время я был в глубине своих изобретательных сил и больше думал над математикой и философией, чем раньше», - писал Ньютон. Тогда юный ученый сделал практически все открытия в области физики и математикиОна открыла закон Всемирного Тяжести и начала с помощью его исследования планет. Она обнаружила, что 3 закона Кеплера об отношении периодов обращения планета и расстояния до Солнца необходимы для того, чтобы предположить силу притяжения. Солнце пропорционально квадрату дальнего расстояния к планете. Но для исследования и выражения законов физики Ньютон должен был заниматься математикой и для этого. В Вулстоне Ньютон, решая задачи касательно кривых, рассчитывая площади кривых фигур, создаёт общее решение таких задач, метод флюксовых производных, флюэнтов, которые Г.В.Лейбница называл дифференциальными. Ньютон рассчитывал производные и интегралы любых степенных функций. Учёный подробно описывает дифференциальные и интегральные исчисления в своей важнейшей работе в математике 1670-1671 годах, опубликованной уже после смерти его. В нём были заложены основы математики. Ньютон находит и формулу различной степени суммы двух строк см. Ньютон является бином, не ограничиваясь натуральными показателями и является суммой бесконечных чисел (см. Ряды). Ньютон объяснил, как использовать ряды в математике. Когда Ньютон вернулся к Кембриджу в 1666 году, он принес в Вулстороп бесчисленный и бесконечный результат своих математико-математических занятий. Он пока не успел их привести в форму, подходящую для публикаций, и с этим не спешил. В 1680 году. Ньютон начинает свою работу над главным сочинением «Математическое начало природной философии», где он задумался о изложении своей системы мира. Книга вышла в историю естествознания и стала крупным событием в истории науки. В нем все величественные строения механики построены на основе аксиома движения, известных теперь как законы Ньютон. Труды И. Ньютона долго определяли путь развития математики и физики. Большая часть классических механик сохранилась надолго в том виде, который создал Ньютон. Закон Всемирного Тяжести постепенно был осознан в качестве единого принципа, который позволяет строить совершенное учение движения небесного тела. Дифференциальное исчислениеДифференциальные исчисления являются разделом математического анализа, где изучается понятие производных и дифференциальных и методы их использования в работе с функциями. В современном научном сообществе однозначно рассматривается разделение науки на античные периоды и новые периоды. Но в чем разница между этими периодами? Что принципиально различало научные подходы Платона и Аристотеля, а также других известных ученых античной эпохи от подходов крупных ученых нового столетия? В реальности разделение на две периоды имеет множество основ. В рамках этой статьи рассмотрим одну, наиболее основную и наглядную основу - формирование дифференциальных исчислений. Благодаря предпосылкам для возникновения этого известного метода в современных науках в трудах философии и математики мы можем проследить четкую границу античного и современного взглядов на науку и однозначно отвечать на вопросы, которые были поставлены в начале этой статьи. Рубеж XVI–XVII веков в истории философии был действительно поворотным моментом для европейской науки, которая совершила качественную скачку. В это время произошел переход от античных наук к новой науке. Не секрет, что «локомотивами» прогресса в этом периоде стали такие выдающиеся ученые, как Рене Декарт, Галилей Галилей, Иоанна Кеплера, Бонавента Кавальеры, Исаак Ньютон. Каждая из них рассказала о своих новых словах в механиках, математиках, астрономиях и других науках. Но не столь важно их вклад в отдельные науки, как вклад в развитие методологии нового времени науки. Плоды творчества этих авторитетных ученых по методологии научных исследований были широко распространены, многие из которых до сих пор остаются основными принципами современных наук. Формирование дифференциальных исчислений как прикладных, а затем и научных методов предшествовало появлению стройной философии Николая Кузанского. В более конкретной роли дифференциальных исчислений прослеживается так называемая теорема «малых событий», развивающаяся параллельно со своей теорией «бесконечных событий». По итогам изложенных рассуждений можно сказать, что диапазон дифференциальных расчетов и основных принципов является границей между античной и новой наукой. Вот именно на этапе развития этого метода произошла переоценка мысли о математике, которая преобразила не только отдельную науку, но методологию в целом науки. ЗаключениеНебольшое произведение Лейбницы, которое появилось в 1684 г., привело к действительному началу исчисления бесконечного малого, давая правилам, достаточно простым для его начала и комбинацией которых была возможность продолжения работы. Она открывает новый этап в математике. Она открывает новый этап в математике. Сама Лейбница уже давно решала многочисленные задачи по исчислению бесконечного малого, что было представлено его произведением. По изучению литературы, посредством письменного и личного общения с другими математическими учеными, он усвоил существовавшие ранее методы, и очень хорошо переработал их. Благодаря этой возможности он смог быстрее двигаться в свою работу. Список использованных источников:https://ru.wikipedia.org/wiki http://www.scienceforum.ru http://sernam.ru/book_e_math http://cyber.econ.spbu.ru |