Модель синхронной машины. Моделирование я. Реферат Синхронная машина с постоянными магнитами Обучающийся 2 курса группы маи203
 Скачать 411.96 Kb. Скачать 411.96 Kb.
|
|
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕНЕТИКИ, БИОТЕХНОЛОГИИ И ИНЖЕНЕРИИ им.Н.И.Вавилова Факультет инженерии и природообустройства Кафедра электрооборудование, энергоснабжение и роботизации Дисциплина: Моделирование электротехнических комплексов Реферат Синхронная машина с постоянными магнитами Выполнил: Обучающийся 2 курса группы М-АИ-203 очной формы обучения Кукин Денис Сергеевич Саратов 2022 г. Содержание1. Принцип работы 4 2. Векторная диаграмма 4 3. Векторная диаграмма и момент СД с неявнополюсным ротором 7 4. Уравнение равновесия статора СДПМ 8 5. Модель электромагнитных процессов СДПМ 10 6. Модель СДПМ в SimInTech 11 Список литературы 13 1. Принцип работыРотор такого двигателя представляет собой постоянный магнит. Ток обмотки статора создает вращающееся магнитное поле статора, магнитные полюса которого притягивают противоположные магнитные полюса ротора. Вследствие этого возникает момент, вращающий ротор вслед за полем статора (Рис.1). 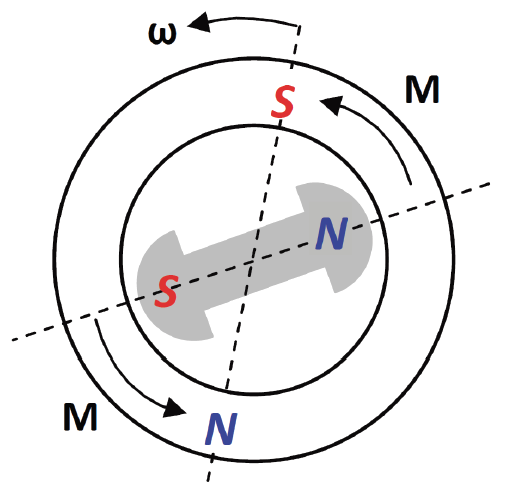 Рисунок 1. 2. Векторная диаграммаНа Рис.2. изображена векторная диаграмма, поясняющая процессы, происходящие в двигателе. Будем рассматривать их во вращающейся системе координат dq, ось d которой ориентирована по потоку ротора.  f Ротор двигателя, являющийся постоянным магнитом, создает потокосцепление ( 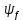 ), равное произведению потока ротора на число витков обмотки статора. Направлен вектор этого потокосцепления по оси ротора (d) от положительного полюса к отрицательному и отстает от вектора то- ка статора ( ), равное произведению потока ротора на число витков обмотки статора. Направлен вектор этого потокосцепления по оси ротора (d) от положительного полюса к отрицательному и отстает от вектора то- ка статора (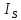 ) на некоторый угол φ. Постоянный поток вращающегося ротора создает в обмотках статора вектор ЭДС ( E ), направленный под прямым углом к потоку и опережающий его на 90º (производная потокосцепления ротора ) на некоторый угол φ. Постоянный поток вращающегося ротора создает в обмотках статора вектор ЭДС ( E ), направленный под прямым углом к потоку и опережающий его на 90º (производная потокосцепления ротора 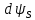 /dt ) /dt )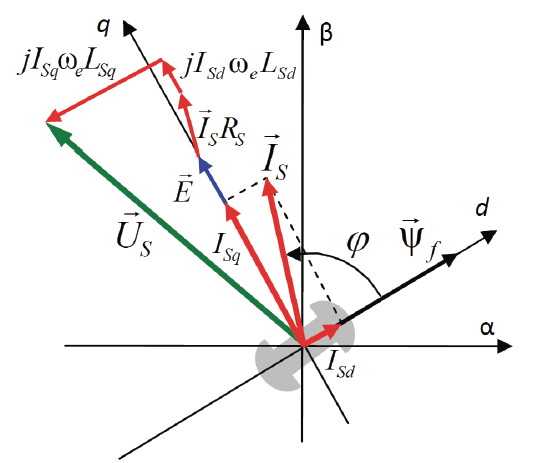 Рисунок 2 – векторная диаграмма Амплитуда вектора ЭДС определяется выражением: 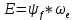 где: 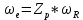 – скорость вращения поля; – скорость вращения поля; 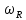 – скорость вращения ротора; – скорость вращения ротора; 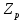 – число пар полюсов двигателя. – число пар полюсов двигателя. Согласно рисунку 2 можно записать следующее векторное соотношение: 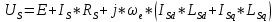 где: 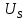 – вектор напряжения статора; – вектор напряжения статора; 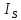 – вектор тока статора, а – вектор тока статора, а 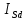 и и 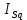 – его составляющие; – его составляющие; 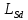 и и 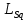 – индуктивность статора по осям d и q; – индуктивность статора по осям d и q; 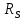 – сопротивление статора. – сопротивление статора.В соответствии с рис.2, вектор статорного напряжения уравновешивается вектором ЭДС и падением напряжения на активном ( 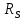 ) и реактивном ( ) и реактивном (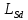 , ,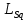 ) сопротивлениях статорной обмотки. ) сопротивлениях статорной обмотки.Момент двигателя возникает вследствие того, что на заряженную частицу, движущуюся в магнитном поле, действует некая сила (сила Лоренца). Вывод формулы, определяющей момент, можно сделать исходя из соотношений, описывающих мощность двигателя, например так, как это сделано в книге Г.Г. Соколовского Но мы пойдем другим путем (более векторным) и будем считать, что момент возникает в результате силового взаимодействия между векторами тока и потокосцепления статора. А именно, что момент определяется векторным произведением действующих значений этих векторов. Это действительно так, и в дальнейшем расчетная формула для момента получается точно такой же, как и при вышеупомянутом подходе нахождения момента через мощность. Учитывая фазность и число пар полюсов двигателя ( 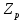 ) можно записать следующее выражение для вычисления момента СДПМ: ) можно записать следующее выражение для вычисления момента СДПМ: 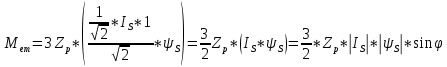 где: 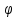 – угол между векторами. – угол между векторами.Запишем формулу для вычисления момента в системе dq. 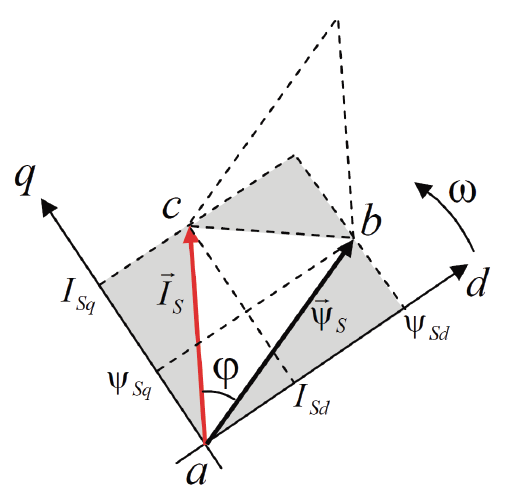 Рисунок 3. Как известно, величина векторного произведения двух векторов равна площади параллелограмма, сторонами которого они являются. Запишем площадь параллелограмма со сторонами 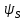 и и 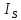 через проекции этих векторов на оси dq. Для этого вычислим удвоенную площадь треугольника abc: через проекции этих векторов на оси dq. Для этого вычислим удвоенную площадь треугольника abc: 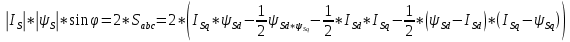 = =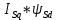 – – 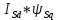 где: 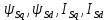 – проекции потокосцепления и тока статора на оси d и q. – проекции потокосцепления и тока статора на оси d и q. Соответственно, формула для расчета электромагнитного момента СДПМ в системе dq будет выглядеть так: 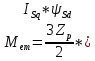 – – 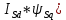 Имея в виду, что потокосцепление статора, в свою очередь, формируется током в индуктивности статора и потоком ротора, запишем выражения для его d и q составляющих: 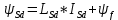 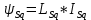 С учётом этих выражений напишем уравнение для вычисления момента в виде: 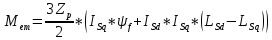 3. Векторная диаграмма и момент СД с неявнополюсным роторомРотор синхронного двигателя с неявнополюсным ротором устроен так, что индуктивности статора по осям d и q у него одинаковы. Управление именно таким двигателем является типовой, наиболее часто встречающейся задачей. Так как 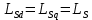 , выражение для момента двигателя упростится и запишется в виде: , выражение для момента двигателя упростится и запишется в виде: 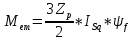 Глядя на выражение, можно констатировать, что при фиксированном потоке магнита - ротора момент зависит только от q – составляющей статорного тока. То есть d – составляющая тока является паразитной - момента она не вызывает, а к потерям в меди статора приводит. Следовательно, при регулировании момента логично поддерживать ее равной нулю, ориентируя вектор тока статора по оси q. Обычно так и поступают. Векторная диаграмма для этого случая представлена на рис. 4. 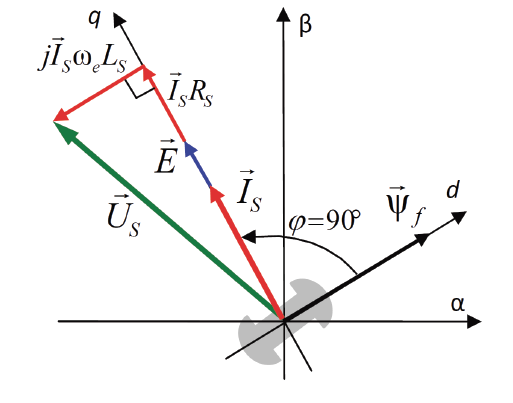 Рисунок 4. 4. Уравнение равновесия статора СДПМКак известно, напряжение на катушке индуктивности равно сумме ЭДС индукции и падения напряжения на активном сопротивлении катушки, а ЭДС индукции равна производной от суммарного потока (потокосцепления) катушки. Статор двигателя является трехфазной катушкой индуктивности, и при условии пренебрежения магнитными потерями, в неподвижной системе координат для него можно записать следующее простое выражение: 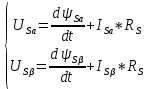 Это выражение называется уравнением равновесия статора. Учитывая, что потокосцепление - это произведение тока на индуктивность, перепишем эти уравнения в системе координат dq, вращающейся вместе с полем. 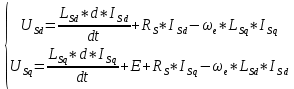 Рассмотрим этот переход подробнее. Разберемся с дифференциалами потокосцепления статора по осям d и q. Потокосцепление в статоре создается двумя источниками: - потоком ротора - током в индуктивности статора. Соответственно дифференциал потокосцепления статора будет зависеть от дифференциалов потокосцепления ротора и тока статора. Кроме того, в нем еще будет некоторая составляющая, вызванная вращением системы координат. Поскольку изменение потока ротора по оси d отсутствует, дифференциал потокосцепления статора по этой оси имеет только две составляющие: 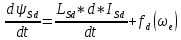 где: 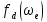 – составляющая дифференциала потока, вызываемая вращением системы координат. – составляющая дифференциала потока, вызываемая вращением системы координат. А дифференциала потокосцепления статора по оси q имеет все три составляющие, причём дифференциал потокосцепления ротора по этой оси есть не что иное, как ЭДС (Е): 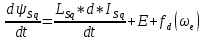 Соответственно, 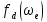 – составляющая дифференциала потокосцепления статора, вызываемая вращением системы координат. – составляющая дифференциала потокосцепления статора, вызываемая вращением системы координат. Известно, что производная вектора, вращающегося со скоростью ωe, есть вектор, амплитуда которого равна линейной скорости конца вращающегося вектора. Направлен вектор производной будет в сторону вращения, по касательной к траектории. Таким образом, для нахождения производной вращающегося вектора его амплитуду надо умножить на ωe и повернуть полученный вектор на π/2 в сторону вращения. Так как с частотой ωe у нас вращается система координат, то для нахождения производной вектора, вызванной этим вращением, поворот вектора на π/2 надо делать в сторону, противоположную вращению. Пусть положительным направлением вращения системы считается вращение против часовой стрелки Тогда рис.5 поясняет образование составляющих дифференциала тока статора, связанных с вращением системы координат. 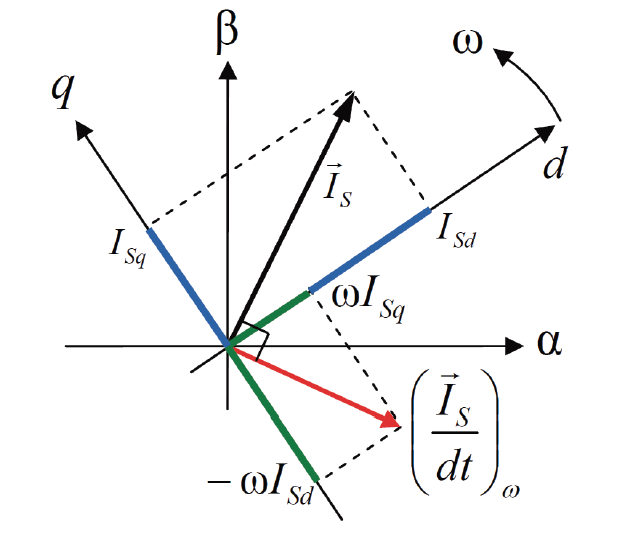 Рисунок 5. Глядя на рисунок и учитывая, что потокосцепление – это ток, умноженный на индуктивность, можно записать: 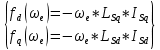 5. Модель электромагнитных процессов СДПМУчитывая, что E= 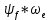 , запишем уравнение относительно дифференциалов токов и дополним их уравнением момента: , запишем уравнение относительно дифференциалов токов и дополним их уравнением момента: 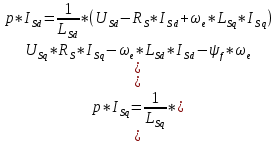 По этому уравнению можно построить модель электромагнитных процессов двигателя, так как это показано на рис.6. 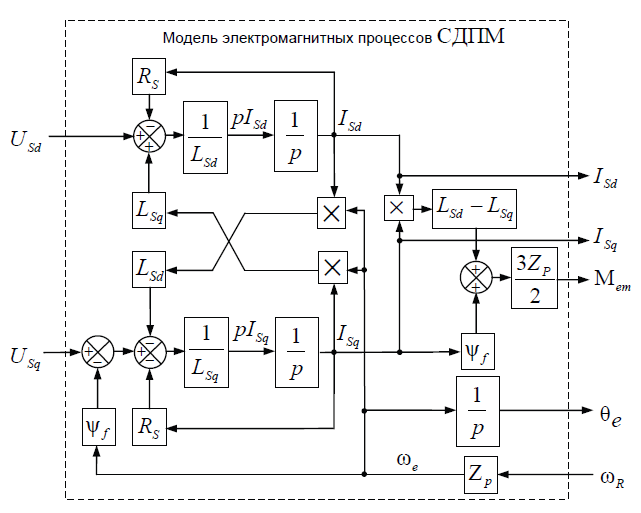 Рисунок 6. 6. Модель СДПМ в SimInTechМодель СДПМ в SimInTech (Рис.7) содержит структуру, изображенную на Рис.6, дополненную следующими узлами: - преобразователями координат, связывающими величины токов и напряжений во вращающейся системе dq с их значениями в трехфазной неподвижной системе координат ABC - блоками управляемых источников тока и измерителей напряжения, осуществляющими стыковку модели с элемента- ми библиотеки «ЭЦ – Динамика». 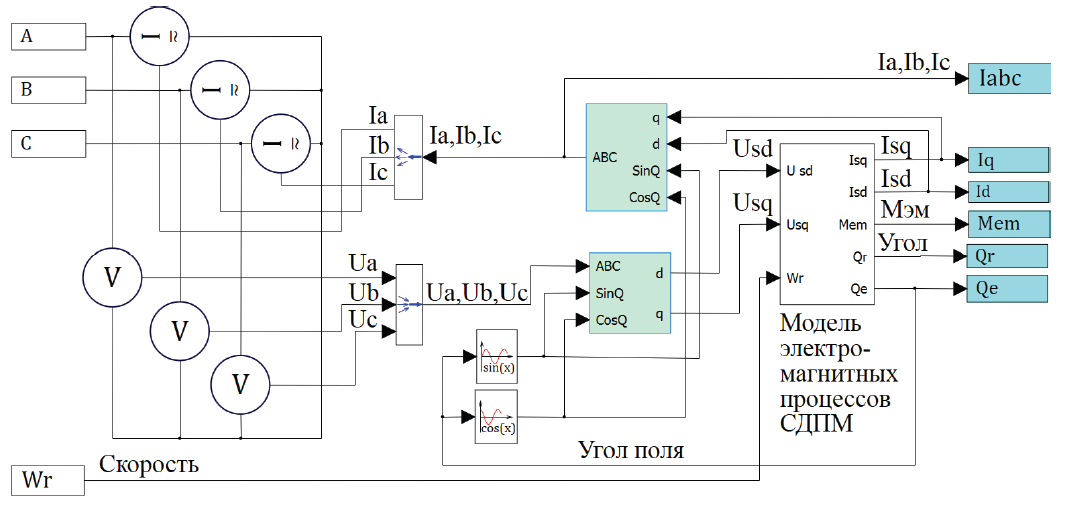 Рисунок 7 – модель СДПМ Сигнал электромагнитного момента двигателя (Мem) в реальности прикладывается к некоторой механической системе, характеризующейся моментами инерции и нагрузки. Соответственно выход электромагнитного момента модели двигателя должен подаваться на модель механической системы, выполненной на элементах библиотеки «Механика», позволяющей моделировать сложные передаточные механизмы и нагрузки. Модель механической системы преобразует сигнал момента в скорость, которая в свою очередь подается на соответствующий вход модели двигателя. Если же двигатель не нагружен, в «Механике» может моделироваться момент инерции ротора и трение в подшипниках. Список литературы1. Г.Г. Соколовский, «Электроприводы переменного тока с частот- ным регулированием», Москва, AKADEMIA 2006. 2. А.Б. Виноградов, «Векторное управление электроприводами пере- менного тока», Федеральное агентство по образованию Государ- ственное образовательное учреждение высшего профессионально- го образования «Ивановский государственный энергетический университет имени В.И. Ленина», Иваново 2008. 3. Ю.Н, Калачев, «Векторное регулирование (заметки практика)», ЭФО, 2013. 4. Zhenyu Yu, Application Report, SPRA524, Digital Signal Processing Solutions March 1999, Space-Vector PWM With TMS320C24x/F24x Using Hardware and Software Determined Switching Patterns |
