КР_3. Реферат синтез нечіткого регулятора для системи управління процесом сушіння капілярнопористих матеріалів

• Название: Реферат синтез нечіткого регулятора для системи управління процесом сушіння капілярнопористих матеріалів
• Дата: 23.09.2022
• Размер: 156.8 Kb.
• Имя файла: КР_3.docx
• Тип: Реферат; #692608

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
Івано-Франківський національно технічний університет нафти і газу

Кафедра автоматизації та комп’ютерно-інтегрованих технологій

Реферат

СИНТЕЗ НЕЧІТКОГО РЕГУЛЯТОРА ДЛЯ СИСТЕМИ УПРАВЛІННЯ

ПРОЦЕСОМ СУШІННЯ КАПІЛЯРНО-ПОРИСТИХ МАТЕРІАЛІВ

Виконав студент групи АКП-21-1К

Корчинський О. Р.

Перевірив викладач:

Борин В. С.

Івано-Франківськ

2022

Процес дифузії в цукровому виробництві є одним з найважливіших технологічних процесів, в результаті якого відбуваються якісні зміни вихідної сировини з деякими втратами цукру у відходах, що складають значні збитки. В зв’язку з цим питання інтенсифікації цього процесу представляє великий практичний та науковий інтерес. Рішення цього питання потребує якісної та кількісної оцінки впливу технологічних факторів на нього. Більшість вітчизняних цукрових виробництв оснащено колонними дифузійними установками(КДУ), що складаються з двох окремих апаратів – ошпарювач та колонний дифузійний апарат.

КДУ цукрового заводу, є нестаціонарним технологічним агрегатом, що характеризується невизначеністю параметрів, тому застосування традиційних одноконтурних систем регулювання її роботи не дає бажаного ефекту. В зв’язку з тим, що дифузійна установка є багатозв’язним об’єктом, що працює в умовах невизначеності, недостатня точність підтримання технологічного режиму приводить до збільшення витрати енергоносіїв та втрат цукру в жомі. В процесі функціонування колонної дифузійної установки її параметри змінюються в досить широкому діапазоні, що суттєво впливає на зміну постійних часу та коефіцієнтів передачі об’єкта, тому можуть з’явитися випадки, коли система втратить стійкість. При втраті стійкості системи різко підвищується температура сокостружкової суміші, що призводить до розварювання стружки та припинення фізико-хімічного процесу дифузії. Як правило, на підприємствах підтримання заданого температурного режиму здійснюється локальними регуляторами типу П та ПІ, але за рахунок зв'язності температур в різних зонах регулювання кожної з них окремо приводить до відхилень інших та затягування перехідних процесів. Збільшення часу перехідних процесів також веде до відхилення температур від регламенту та втрати цукру.

Останнім часом з’явилося багато публікацій стосовно робастної стійкості об’єктів керування як в суто теоретичному плані так і багато практичних застосувань. В класичній теорії керування є один підхід, а саме синтез модальних регуляторів, який вирішує сумісну задачу. При синтезі модального регулятора наперед задаються бажані корені характеристичного поліному системи, при чому обґрунтовуються ці значення необхідною якістю перехідних процесів в системі та наявністю невизначеностей, що не описуються. Перевірка робастної стійкості проводиться для системи, що задана класом невизначеності, що досить чітко описується математично.

Математичний опис об’єкта. Вимоги до системи керування

Для створення необхідної системи керування технологічним об’єктом (КДА) необхідно обрати математичну модель об’єкта, вибрати корені характеристичного поліному системи, синтезувати регулятор та перевірити якість системи, описати невизначеності в об’єкті, визначити запас стійкості системи, а при необхідності скоригувати задані корені. Математична модель теплообмінної частини дифузійного відділення задана у вигляді:



Де – вектор координат стану, що складається відповідно з температури пари, що поступає в підігрівники, температур соку та барометричної води після підігрівників, температури сокостружкової суміші на виході з ошпарювала та температур сокостружкової суміші по трьом зонам колонного апарату;

T G п G п G п u  G   ,  3 , 2 , 1 – вектор керування, що складається відповідно з витрат пари, що надходять у три підігрівники соку та витрати сокостружки, що надходить у середину ошпарювача; y – вектор вимірювань, що складається з 7, 8, 9, 10-ої координат стану x; при незмінних параметрах роботи об’єкта А=А₀, B=B₀, де:



Власні значення матриці номінального об’єкта A0 є цілі та приймають такі числа:



тобто об’єкт має самовирівнювання, але запас стійкості занадто малий – 0.021. Більш того, даний об’єкт є надстійким.

Аналіз впливу режимних параметрів дифузійної установки на вміст цукру в жомі, якість та кількість одержуваного дифузійного соку і багато інших показників показав, що процес вилучення цукру зі стружки поліпшується зі збільшенням відкачування і тривалості висолоджування, підвищенням температури та збільшенням довжини стружки. Очевидно, що для стабілізації цих параметрів потрібно підтримувати температурний режим роботи установки відповідно оптимальному технологічному режиму в змінюваних умовах. Отже, розроблена ефективна системи керування теплообмінною частиною КДУ, повинна забезпечувати підтримання температури сокостружкової суміші на виході з ошпарювача та температур в трьох зонах колонного дифузійного апарату відповідно обраного режиму роботи в умовах невизначеності. Відмітимо, що на практиці в КДУ температури в зонах апарату та температура сокостружкової суміші на виході з ошпарювача регулюються непрямим методом, тому існує час запізнення між зміною витрати пари на підігрівниках і зміною температур по зонам КДУ, причому ці технологічні змінні зв’язані між собою. Як видно з матриці С лише названі чотири температури є виміряними, а регулятор будується у формі зворотного зв’язку за станами системи, тому в системі керування також необхідно застосувати спостерігач.

Щоб мінімізувати перехідні процеси в замкненій системі відносно збурення та зміни завдання відповідно технологічному регламенту найкраще підходить біноміальний розподіл коренів, тобто – швидкодія системи, що співвідноситься з часом перехідного процесу за формулою . Якщо час перехідного процесу то швидкодія Але деякі власні значення матриці об’єкта менші за –₀ , тому при завданні необхідних коренів замкненої системи змінюємо лише другий корінь.

Невизначеності в об’єкті

КДУ функціонує в невизначених умовах. Невизначеність роботи КДУ викликана змінними коефіцієнтами тепло- та масообмінних процесів та значною кількістю некерованих параметрів. Вміст цукру в жомі, якість та кількість одержуваного дифузійного соку і багато інших показників залежать від наступних режимних параметрів дифузійної установки: еквівалентної товщини бурякової стружки, коефіцієнта дифузії цукру в буряковій тканині, коефіцієнта нерівномірності роботи дифузійної установки, місяця виробничого сезону, цукристості стружки, питомого навантаження стружкою колонного апарату, доброякісністю дифузійного соку, витрати дифузійного соку на виробництво, витрати стружки, температури потоків вхідної стружки, вихідного соку, пари та сокостружки.

Вище перераховані змінні в свою чергу розділяються на керуючі (які змінює оператор або система автоматизації) та некеровані (які приймають випадкові значення). Керуючими параметрами є: еквівалентна товщина бурякової стружки, питоме навантаження стружкою колонного апарату, витрати соку та стружки, а також температури потоків, інші параметри – некеровані, що створює проблему при управління процесом дифузії. Також на об’єкт діють збурення, величина та характер яких залежать від специфіки процесу, режиму роботи теплових споживачів та конструктивних характеристик апаратури.

Невизначеність виявляється при складанні математичної моделі КДУ та при введенні спрощуючих припущень. Зокрема, для математичної моделі були прийняті такі припущення: об'єкт вважається з зосередженими параметрами; дифузійний апарат має ідеальну теплову ізоляцію, тобто нехтуються втрати в навколишнє середовище; приймається в одній ємності постійними питомі теплоємності дифузійного соку та стружки, коефіцієнт теплопередачі та густина сокостружкової суміші; теплова ємність конструкції дифузійного апарату не враховується. Але числові значення постійних часу та коефіцієнтів передачі об’єкта в математичній моделі розраховуються в залежності від значень питомої теплоємності дифузійного соку та стружки, коефіцієнта теплопередачі та густини сокостружкової суміші, що в процесі роботи об’єкта змінюються від 1,1 до 3 разів, тому математична модель не завжди є адекватною об’єкту. Все це підтверджує доцільність застосування робастних систем при управлінні процесом дифузії. Враховуючи назване, матриці об’єкта з невизначеностями перепишуться у формі інтервального матричного сімейства: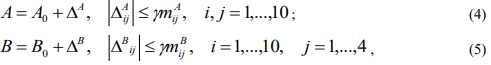



Де – елементи матриць відповідно;   0 – розмах невизначеності; - масштаби зміни елементів матриці А та В відповідно.

Якщо взяти – елементи матриць А₀, В₀ відповідно, то розмах невизначеності  буде вказувати на максимальний відсоток зміни матриць А₀ та В₀ від номінального.

Синтез модального регулятора та робастна стійкість системи

Згідно з алгоритмом модального синтезу для багатовимірних систем регулятор отримується у формі зворотного зв’язку за станом системи:



де K – матричний коефіцієнт підсилення регулятора: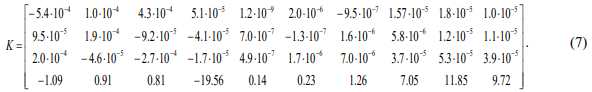



Округлюючи отримані значення до третього числа після коми, що створює додаткову похибку, отримуємо перехідні процеси відносно зміни завдання для номінальної системи (рис., криві 1). Як видно з графіків час перехідних процесів відрізняється від заданого 60 с та складає 80 с, що для КДУ вкладається в технологічний регламент.

При синтезі системи управління з матрицею К замкнена система втратила властивість надстійкості, тобто застосувати готові формули неможливо, тому далі використовується теорія ймовірності.

Шляхом рівномірної випадкової генерації номінальної матриці об’єкта А (5) в межах заданої невизначеності (матриця К не змінювалася) визначений найбільший розмах невизначеності при якому система залишається стійкою, що складає   0.18 з ймовірністю 0.98, при чому найменший запас стійкості складає 0.037. Отримані граничні перехідні процеси системи управління (рис.1, криві 2...N, де N – кількість випадкових генерацій, N>200) та визначено, що час перехідного процесу системи з невизначеностями не змінився, максимальна динамічна похибка не перевищує 22% від динамічної похибки номінальної системи та в деяких випадках виникає статична похибка, що не перевищує складає 0.3 0C для всіх реалізацій.

Для системи з параметричними невизначеностями матриць А та В (4), (5) виявлено, що розмах невизначеності, при якій система залишається стійкою, зменшився і складає   0.1 з ймовірністю 0.98, найменший запас стійкості складає 0.034, характер перехідних процесів не змінився.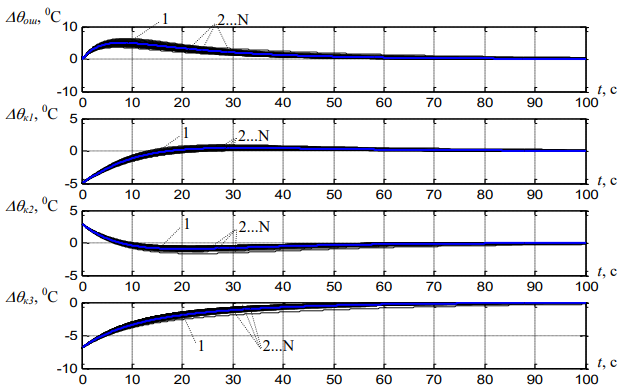



Рисунок-1 Перехідні процеси відносно зміни завдання:

1-номінальна система; 2-N система з невизначеностями

Проведені дослідження показали, що отриманий максимальний розмах невизначеності 10% вкладається в змінювані умови роботи об’єкта та якість перехідних процесів задовільна, тобто синтезована система є ефективною та не потребує зміни коренів характеристичного поліному.

Висновок

КДУ функціонує в умовах параметричних невизначеностей, тому при синтезі системи керування цим об’єктом необхідно перевіряти якість та стійкість системи. Невизначеності КДУ можуть бути описані інтервальними залежностями, але крім зміни матриці А в математичній моделі (1) змінюється також і матриця В. Формули наведені в не можуть бути застосовані для дослідження робастної стійкості системи, тому використовується ймовірнісний підхід. Для КДУ визначений максимальний розмах невизначеності, при якому система з параметричними невизначеностями (4)-(5) залишається стійкою та має задовільну якість перехідних процесів, а отже, система керування є ефективною.