реферат отправка. Реферат тема Проверил 2022 г. Содержание введение
 Скачать 0.58 Mb.
|
|
РЕФЕРАТ Тема: Выполнил: Проверил: 2022 г. СОДЕРЖАНИЕ Введение………………………………………………………………………….3 LDPC-code – история создания………………………………………….……..4 Преимущества LDPC-кодов, их применение и перспективы развития…….10 Алгоритм Belief propagation…………………………………………….……..12 Заключение……………………………………………………………………..24 Список используемой литературы……………………………………………25 Введение В настоящее время происходит интенсивное развитие различных цифровых систем передачи данных, таких как космическая, спутниковая, мобильная связь и др. Все подобные системы используют для передачи данных беспроводные каналы, в которых на передаваемый сигнал действуют помехи различной физической природы. Это приводит к тому, что принятые данные с достаточно большой вероятностью будут содержать ошибки. В то же время для многих практических приложений допустима лишь очень небольшая доля ошибок в обрабатываемых дискретных данных. В результате возникает проблема обеспечения надежной передачи цифровой информации по каналам с шумами. Важнейший вклад в решение данной проблемы вносит теория помехоустойчивого кодирования. На ее основе разрабатываются методы защиты от ошибок, базирующиеся на применении помехоустойчивых кодов. Использование этих кодов позволяет получить энергетический выигрыш кодирования (ЭВК), который характеризует степень возможного снижения энергетики передачи при кодировании по сравнению с отсутствием кодирования, если достоверность передачи в обоих случаях одинакова. Этот выигрыш можно использовать для улучшения параметров и характеристик многих важных свойств систем передачи данных, например, для уменьшения размеров очень дорогих антенн, повышения дальности связи, увеличения скорости передачи данных, снижения необходимой мощности передатчика и т.д. LDPC-code – история создания Коды с малой плотностью проверок на четность (LDPC-код от англ. Low-density parity-check code, LDPC-code, низкоплотностный код) были впервые предложены Робертом Галлагером и позднее исследовались во многих научных работах. Несмотря на то, что в течение долгого времени LDPC-коды были практически исключены из рассмотрения, в последние годы наблюдается увеличение количества исследований в этой области. Это связано с тем, что, обладая плохим минимальным расстоянием, коды с малой плотностью, тем не менее, обеспечивают высокую степень исправления ошибок при весьма малой сложности их декодирования. Было показано, что с ростом длины некоторые LDPC-коды могут превосходить турбо-коды и приближаться к пропускной способности канала с аддитивным белым гауссовским шумом (АБГШ). Вместе с тем многие предложенные конструкции LDPC-кодов являются циклическими или квазициклическими, что позволяет производить не только быстрое декодирование, но и эффективные процедуры кодирования. Кроме того, даже для LDPC-кодов, не обладающих свойством цикличности, были предложены эффективные процедуры кодирования. В 1948 году Клод Элвуд Шеннон опубликовал свою работу по теории передачи информации. Одним из ключевых результатов работы считается теорема о передачи информации для канала с шумами, которая говорит о возможности свести вероятность ошибки передачи по каналу к минимуму при выборе достаточного большой длины ключевого слова — единицы информации передаваемой по каналу.  Рисунок 1. Упрощённая схема передачи информации по каналу с шумами. При передаче информации её поток разбивается на блоки определённой (чаще всего) длины, которые преобразуются кодером (кодируются) в блоки, называемыми ключевыми словами. Ключевые слова передаются по каналу, возможно с искажениями. На принимающей стороне декодер преобразует ключевые слова в поток информации, исправляя (по возможности) ошибки передачи. Теорема Шеннона утверждает, что при определённых условиях вероятность ошибки декодирования (то есть невозможность декодером исправить ошибку передачи) можно уменьшить, выбрав большую длину ключевого слова. Однако, данная теорема (и работа вообще) не показывает, как можно выбрать большую длину, а точнее как эффективно организовать процесс кодирования и декодирования информации с большой длиной ключевых слов. Если предположить, что в кодере и декодере есть некие таблицы соответствия между входным блоком информации и соответствующим кодовым словом, то такие таблицы будут занимать очень много места. Для двоичного симметричного канала без памяти (если говорить упрощённо, то на вход кодера поступает поток из нулей и единиц) количество различных блоков составляет 2n, где n — количество бит (нулей или единиц) которые будут преобразовываться в одно кодовое слово. Для 8 бит это 256 блоков информации, каждый из которых будет содержать в себе соответствующее кодовое слово. Причём кодовое слово обычно большей длины, так как содержит в себе дополнительные биты для защиты от ошибок передачи данных. Поэтому одним из способов кодирования является использование проверочной матрицы, которые позволяют за одно математическое действие (умножение строки на матрицу) выполнить декодирование кодового слова. Аналогичным образом каждой проверочной матрице соответствует порождающая матрица, аналогичным способом одной операцией умножения строки на матрицу генерирующей кодовой слово. Таким образом, для сравнительно коротких кодовых слов кодеры и декодеры могут просто содержать в памяти все возможные варианты, или даже реализовывать их в виде полупроводниковой схемы. Для большего размера кодового слова эффективнее хранить порождающую и проверочную матрицу. Однако, при длинах блоков в несколько тысяч бит хранение матриц размером, соответственно, в мегабиты, уже становится неэффективным. Одним из способов решения данной проблемы становится использования кодов с малой плотностью проверок на чётность, когда в проверяющей матрице количество единиц сравнительно мало, что позволяет эффективнее организовать процесс хранения матрицы или же напрямую реализовать процесс декодирования с помощью полупроводниковой схемы. Первой работой на эту тему стала работа Роберта Галлагера «Low-Density Parity-Check Codes» 1963 года (основы которой были заложены в его докторской диссертации 1960 года). В работе учёный описал требования к таким кодам, описал возможные способы построения и способы их оценки. Поэтому часто LDPC-коды называют кодами Галлагера. В русской научной литературе коды также называют низкоплотностными кодами или кодами с малой плотностью проверок на чётность. Однако, из-за сложности в реализации кодеров и декодеров эти коды были позабыты. Лишь много позже, с развитием телекоммуникационных технологий, снова возрос интерес к передаче информации с минимальными ошибками. Несмотря на сложность реализации по сравнению с турбо-кодом, отсутствие преград к использованию (незащищённость патентами) сделало LDPC-коды привлекательными для телекоммуникационной отрасли. Появление новых эффективных алгоритмов декодирования стимулировало и повышение интереса к методам построения недвоичных LDPC-кодов. Первоначально построение недвоичных LDPC кодов осуществлялось путем замены ненулевых элементов в проверочной матрице двоичных LDPC-кодов на случайные элементы конечного поля. Позднее Лиин (Lin) предложил методы алгебраического построения квазициклических недвоичных LDPC-кодов (QC NB-LDPC). LDPC-коды становятся востребованными в системах передачи информации, требующих максимальной скорости передачи при ограниченной полосе частот. Основным конкурентом LDPC-кодов на данный момент являются турбо-коды, которые нашли свое применение в системах спутниковой связи, ряде стандартов цифрового телевидения и мобильных системах связи третьего поколения. Однако LDPC-коды по сравнению с турбо-кодами имеют ряд преимуществ. Во-первых, LDPC-коды обгоняют турбо-коды по скорости декодирования. Во-вторых, LDPC-коды более предпочтительны в каналах с меньшими вероятностями ошибок. С развитием методов передачи информации каналы передачи улучшаются, что дает хорошую перспективу для развития LDPC-кодов. Применение методов итеративного декодирования к данным кодам позволяет практически вплотную приблизиться к пропускной способности канала при относительно небольшой сложности реализации. В связи с этим во многих новых стандартах передачи различного рода данных (DVB-S2, 802.11n, 802.16e) именно LDPC- коды рекомендованы для исправления ошибок LDPC- коды представляют собой линейные блоковые коды, задаваемые с помощью проверочной матрицы H, характеризуемой относительно малым (<10) числом единиц в строках и столбцах. Проверочной матрице кода ставится в соответствие граф Таннера, в котором для представления строк и столбцов проверочной матрицы используются определенным образом связанные между собой битовые и проверочные узлы. Например, для кода с матрицей H с рисунке 2. 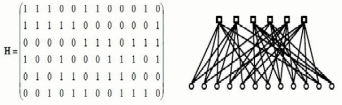 Рисунок 2. Проверочная матрица и граф Таннера LDPC- кода Для декодирования LDPC- кодов обычно используются разновидности sum-product и min-sum алгоритмов, работающих с графом Таннера кода. Данные алгоритмы отличаются сложностью реализации и эффективностью декодирования. В основе работы данных методов лежит итеративный обмен мягкими решениями между битовыми (нижними на рис. 2) и проверочными (верхними на рис. 2) узлами графа кода. При правильном выборе кода (проверочной матрицы) удается получить близкие к оптимальным результаты. Данный алгоритм позволяет получить достаточно хорошие результаты при меньшей сложности реализации.  Рис. 3. Характеристики малоизбыточных помехоустойчивых кодов Пояснения к рисунку 3: РС+АВ(R=0.87,n=16К)» - характеристики каскадного кода, состоящего из кода Рида-Соломона и сверточного кода с общей кодовой скоростью R=0.87 и длиной блока порядка 16 тысяч битов. Многопороговые декодеры (МПД) TCC- Turbo Convolutional Code- турбо- код TPC- Turbo Product Code- турбо- коды произведения LDPC-коды Характеристики малоизбыточных LDPC- кодов, применяемых в стандарте DVB-S2, представлены на рис. 3 кривой «4» LDPC(R=0.88,n=16K)». И при такой кодовой скорости эффективность LDPC близка к предельной.  Рисунок 4. Характеристики помехоустойчивых кодов с R≈1/2 Пояснения к рисунку 4: Декодер Витерби Последовательный декодер Код Рида-Соломона (РС) Многопороговые декодеры (МПД) МПД (ИКИ)- приведены характеристики декодера МПД сверточного кода с 40 итерациями декодирования МПД+КК3 показаны возможности каскадной схемы, использующей МПД во внутренних каскадах МПД+НЭК- МПД алгоритмы для каналов с неравномерной энергетикой TCC- Turbo Convolutional Code- турбо- код TPC- Turbo Product Code- турбо- коды произведения LDPC-коды кода длиной 1000000 битов характеристики используемых в стандартах IEEE 802.16e и DVB-S2 LDPC кодов длиной 2304 и 64800. На рисунке 4 кривой «10» LDPC(n=1000000)» показаны характеристики очень длинного LDPC кода длиной 1000000 битов. Видно, что данный код способен работать примерно в 0.1 дБ от пропускной способности канала, хотя, конечно, его реализация слишком сложна для практического применения. Характеристики используемых в стандартах IEEE 802.16e и DVB-S2 LDPC кодов длиной 2304 и 64800 битов представлены на рис. 4 кривыми «11» 802.16e LDPC(n=2304)» и «12» DVB-S2 LDPC(n=64800)». Видно, что данные коды показывают сопоставимую с турбо- кодами эффективность, но при этом сложность их реализации оказывается в несколько раз меньшей. Следует заметить, что представленные для турбо и LDPC кодов результаты относились к наилучшим алгоритмам их декодирования, работающим с неквантованными решениями демодулятора. При аппаратной реализации декодера часто из-за различных ограничений это оказывается недопустимым. При переходе к более простым алгоритмам, работающим с квантованными на несколько уровней решениям демодулятора возможны потери от 0.5 до 1 дБ и даже более. Характеристики же многопороговые декодеры (МПД) и остальных алгоритмов получены с учетом требований аппаратной реализации. Преимущества LDPC-кодов, их применение и перспективы развития LDPC-коды в современных системах передачи информации занимают нишу, аналогичную турбо-кодам. Оба эти класса кодов используются в системах, где требуются повышенные скорости передачи данных при ограниченной полосе пропускания канала. К числу таких систем можно отнести, например, спутниковую связь, цифровое телевидение (в том числе высокой четкости), а также каналы передачи в электронно-вычислительных машинах и их сетях. LDPC-кодеры могут обеспечивать поистине колоссальную скорость передачи данных (до 40 Гб/с), что обусловлено простотой их реализации. Наиболее быстрыми декодерами разумно было бы считать многопороговые декодеры (МПД), декодирующие по одноименному алгоритму, о котором говорилось выше. В МПД могут легко декодироваться длинные коды, в широком диапазоне кодовых скоростей при использовании как жесткого, так и мягкого модемов. При этом МПД выполняет только простейшие операции сложения и сравнения небольших целых чисел, что обуславливает его крайнюю простоту при всех вариантах программной или аппаратной реализации. Например, МПД может быть реализован с использованием линейных сдвиговых регистров – самых быстрых аппаратных элементов. Следует отметить, что LDPC-кодирование не является сугубо теоретической разработкой, а уже активно используется и введено в некоторые стандарты. Например, в 2003г. LDPC-код вместо турбо-кода стал частью стандарта DVB-S2 спутниковой передачи данных для цифрового телевидения. Аналогичная замена произошла и в стандарте DVB-T2 для цифрового наземного телевизионного вещания. Также LDPC-коды вошли в стандарт IEEE 802.3an сети Ethernet 10G и другие. По результатам исследования среди кодов для включения в стандарт DVB-S2 были отмечены следующие преимущества: отставание от границы Шеннона всего на 0,6–0,8 дБ; преимущество на 0,3 дБ по сравнению с лучшим из представленных турбо-кодов; преимущество на 2,5–3,0 дБ, т. е. 30-процентный прирост в мощности, по сравнению со стандартом DVB-S. Были проведены моделирование работы недвоичных LDPC-кодов и сравнение их производительности с производительностью кодов Рида–Соломона. Результаты моделирования показали, что недвоичные LDPC-коды имеют существенное преимущество над кодами Рида–Соломона. Это преимущество увеличивается по мере увеличения длины кода и разрядности символа.  Рисунок. 5. Сравнение производительности NB-LDPC и кодов Рида–Соломона при средней длине блока Далее рассмотрим алгоритм алгоритмов декодирования — алгоритма Belief propagation (aka SPA — Sum-product algorithm) Алгоритм Belief propagation Распространение убеждения, также известное как передача сообщения сумма-произведение, представляет собой передачу сообщений алгоритм для выполнения вывода на графических моделях, таких как байесовские сети и случайные поля Маркова. Он вычисляет маргинальное распределение для каждого ненаблюдаемого узла (или переменной) в зависимости от любых наблюдаемых узлов (или переменных). Распространение веры обычно используется в искусственном интеллекте и теории информации и продемонстрировало эмпирический успех во многих приложениях, включая коды проверки четности с низкой плотностью, турбо коды, приближение свободной энергии и выполнимость.Алгоритм был впервые предложен Judea Pearl в 1982 году, который сформулировал его как алгоритм точного вывода на деревья, который позже был расширен до многодеревьев. Хотя он не является точным на общих графиках, он оказался полезным приближенным алгоритмом. Если X = {X i } - это набор дискретных случайные величины с соединением функцией масс p, предельное распределение одного X i - это просто суммирование p по всем остальным переменным: p X i (xi) = ∑ x ′: xi ′ = xip (x ′). {\ displaystyle p_ {X_ {i}} (x_ {i}) = \ sum _ {\ mathbf {x} ': x' _ {i} = x_ {i}} p (\ mathbf {x} '). }  Однако это быстро становится недопустимым с точки зрения вычислений: если имеется 100 двоичных переменных, то нужно суммировать более 2 ≈ 6,338 × 10 возможных значений. Используя структуру многодерева, распространение убеждений позволяет намного более эффективно вычислять маргинальные значения. Варианты алгоритма распространения убеждений существуют для нескольких типов графических моделей (в частности, байесовских сетей и марковских случайных полей ). Мы описываем здесь вариант, который работает на факторном графике . Факторный граф - это двудольный граф , содержащий узлы, соответствующие переменным V и факторам F, с ребрами между переменными и факторами, в которых они появляются. Мы можем записать совместную функцию масс: p (x) = ∏ a ∈ F fa (xa) {\ displaystyle p (\ mathbf {x}) = \ prod _ {a \ in F} f_ {a} ( \ mathbf {x} _ {a})} где xa – это вектор соседних узлов переменных к факторному узлу a. Любая байесовская сеть или случайное поле Маркова может быть представлена в виде факторного графа, используя коэффициент для каждого узла с его родителями или коэффициент для каждого узла с его окрестностями соответственно. Алгоритм работает, передавая функции с действительным знаком, называемые сообщениями, вместе с ребрами между скрытыми узлами. Точнее, если v - переменный узел, а a - факторный узел, связанный с v в факторном графе, сообщения от v до a, (обозначаются μ v → a {\ displaystyle \ mu _ {v \ to a}} ) и от a до v (μ a → v {\ displaystyle \ mu _ {a \ to v}} ) -являются функциями с действительным знаком, domain - это Dom (v), набор значений, которые может принимать случайная величина, связанная с v. Эти сообщения содержат «влияние», которое одна переменная оказывает на другую. Сообщения вычисляются по-разному в зависимости от того, является ли узел, получающий сообщение, узлом переменной или узлом фактора. Сохранение той же записи:Сообщение от переменной узла v к факторному узлу a является продуктом сообщений от всех других соседних факторных узлов (кроме получателя; в качестве альтернативы можно сказать, что получатель отправляет как сообщение, постоянная функция равна к «1»): ∀ xv ∈ D om (v), μ v → a (xv) = ∏ a ∗ ∈ N (v) ∖ {a} μ a ∗ → v (xv). {\ Displaystyle \ forall x_ {v} \ in Dom (v), \; \ mu _ {v \ to a} (x_ {v}) = \ prod _ {a ^ {*} \ in N (v) \ setminus \ {a \}} \ mu _ {a ^ {*} \ to v} (x_ {v}).} где N (v) - это набор соседних (факторных) узлов для v. Если N (v) ∖ {a} {\ displaystyle N (v) \ setminus \ {a \}} пусто, тогда μ v → a (xv) {\ displaystyle \ mu _ {v \ to a} (x_ {v})} устанавливается на равномерное распределение.Сообщение от факторного узла a до переменного узла v является произведением фактора с сообщениями от всех других узлов, маргинализовано по всем переменным, кроме одной, связанной с v: ∀ xv ∈ D om (v), μ a → v (xv) = ∑ xa ′: xv ′ = xvfa (xa ′) ∏ v ∗ ∈ N (a) ∖ {v} μ v ∗ → a (xv ∗ ′). {\ displaystyle \ forall x_ {v} \ in Dom (v), \; \ mu _ {a \ to v} (x_ {v}) = \ sum _ {\ mathbf {x} '_ {a}: x '_ {v} = x_ {v}} f_ {a} (\ mathbf {x}' _ {a}) \ prod _ {v ^ {*} \ in N (a) \ setminus \ {v \}} \ mu _ {v ^ {*} \ to a} (x '_ {v ^ {*}}).} где N (a) - это набор соседних (переменных) узлов для a. Если N (a) ∖ {v} {\ displaystyle N (a) \ setminus \ {v \}} пусто, то μ a → v (xv) = fa (xv) {\ displaystyle \ mu _ {a \ to v} (x_ {v}) = f_ {a} (x_ {v})} , поскольку в этом случае xv = xa {\ displaystyle x_ {v} = x_ {a}} .Как показывает предыдущая формула: полная маргинализация сводится к сумме произведений более простых условий, чем те, которые присутствуют в полном совместном распределении. По этой причине он называется алгоритмом сумм-произведений. При типичном запуске каждое сообщение будет обновляться итеративно из предыдущего значения соседних сообщений. Для обновления сообщений можно использовать другое расписание. В случае, когда графическая модель представляет собой дерево, оптимальное планирование позволяет достичь сходимости после вычисления каждого сообщения только один раз (см. Следующий подраздел). Когда факторный граф имеет циклы, такого оптимального расписания не существует, и типичным выбором является одновременное обновление всех сообщений на каждой итерации. После сходимости (если сходимость произошла) предполагаемое предельное распределение каждого узла пропорционально произведению всех сообщений от смежных факторов (без нормировочной константы): p X v (xv) ∝ ∏ a ∈ N (v) μ a → v (xv). {\ displaystyle p_ {X_ {v}} (x_ {v}) \ propto \ prod _ {a \ in N (v)} \ mu _ {a \ to v} (x_ {v}).} Аналогичным образом, оцененное совместное маргинальное распределение набора переменных, принадлежащих одному фактору, пропорционально произведению фактора и сообщений от переменных: p X a (xa) ∝ fa (xa) ∏ v ∈ N ( а) μ v → a (xv). {\ displaystyle p_ {X_ {a}} (\ mathbf {x} _ {a}) \ propto f_ {a} (\ mathbf {x} _ {a}) \ prod _ {v \ in N (a)} \ mu _ {v \ to a} (x_ {v}).} В случае, когда факторный граф является ациклическим (то есть является деревом или лесом), эти оцененные маргиналы фактически сходятся к истинным маргиналам в конечное количество итераций. Это можно показать с помощью математической индукции. Точного алгоритма для деревьев В случае, когда граф факторов является деревом, алгоритм распространения убеждений вычислит точные маргиналы. Кроме того, при правильном планировании обновлений сообщения оно прекратится после 2 шагов. Это оптимальное планирование можно описать следующим образом: Перед запуском граф ориентируется путем назначения одного узла в качестве корня; любой некорневой узел, который связан только с одним другим узлом, называется листом. На первом этапе сообщения передаются внутрь: начиная с листьев, каждый узел передает сообщение вдоль (уникального) края к корневому узлу. Древовидная структура гарантирует, что можно получить сообщения от всех других прилегающих узлов до передачи сообщения. Это продолжается до тех пор, пока корень не получит сообщения от всех своих соседних узлов. Второй шаг включает передачу сообщений обратно: начиная с корня, сообщения передаются в обратном направлении. Алгоритм завершается, когда все листья получили свои сообщения. Приближенный алгоритм для общих графов- изначально был разработан для ациклических графических моделей, было обнаружено, что алгоритм распространения веры может использоваться в общих графах. Затем алгоритм иногда называют зацикленным распространением убеждений, потому что графы обычно содержат циклы или циклы. Инициализация и планирование обновлений сообщений должны быть немного скорректированы (по сравнению с ранее описанным расписанием для ациклических графов), потому что графы могут не содержать листьев. Вместо этого каждый инициализирует все сообщения переменных в 1 и использует те же определения сообщений, что и выше, обновляя все сообщения на каждой итерации (хотя сообщения, поступающие из известных листьев или подграфов с древовидной структурой, могут больше не нуждаться в обновлении после достаточных итераций). Легко показать, что в дереве определения сообщений этой модифицированной процедуры будут сходиться к набору определений сообщений, приведенных выше, в течение количества итераций, равных диаметру дерева. Точные условия, при которых будет сходиться ненадежное распространение убеждений, до сих пор не совсем понятны; известно, что на графах, содержащих один цикл, в большинстве случаев он сходится, но полученные вероятности могут быть неверными. Существует несколько достаточных (но не необходимых) условий для сходимости зацикленного распространения убеждений к единственной фиксированной точке. Существуют графы, которые не могут сойтись или которые будут колебаться между несколькими состояниями при повторяющихся итерациях. Такие методы, как диаграммы ВЫХОДА, могут предоставить приблизительную визуализацию прогресса распространения убеждений и приблизительный тест на сходимость. Существуют и другие приближенные методы маргинализации, включая вариационные методы и методы Монте-Карло. Один метод точной маргинализации в общих графах называется алгоритмом дерева соединений, что является простым распространением убеждений на модифицированном графе, который гарантированно является деревом. Основная предпосылка - исключить циклы путем их кластеризации в отдельные узлы. Связанные алгоритмы и проблемы сложности - подобный алгоритм обычно называют алгоритмом Витерби, но также известен как частный случай max-product или min- алгоритм суммы, который решает связанную проблему максимизации или наиболее вероятного объяснения. Вместо попытки решить маргинальное значение здесь цель состоит в том, чтобы найти значения x {\ displaystyle \ mathbf {x}} , которые максимизируют глобальную функцию (т.е. наиболее вероятные значения в вероятностной настройке), и его можно определить с помощью arg max :* arg max xg (x). {\ displaystyle \ operatorname {*} {\ arg \ max} _ {\ mathbf {x}} g (\ mathbf {x}).} Алгоритм, который решает эту проблему, почти идентичен распространению убеждений, с суммы заменены на максимумы в определениях. Стоит отметить, что проблемы вывода, такие как маргинализация и максимизация, NP-трудны для точного и приближенного решения (по крайней мере, для относительная ошибка ) в графической модели. Точнее, проблема маргинализации, определенная выше, - это # P-complete, а максимизация - NP-complete. Использование памяти для распространения убеждений может быть уменьшено за счет использования алгоритма Island. (с небольшими затратами по времени). Связь со свободной энергией - алгоритм суммы-произведения связан с вычислением свободной энергии в термодинамике. Пусть Z будет статистической суммой. Распределение вероятностей P (X) = 1 Z ∏ fjfj (xj) {\ displaystyle P (\ mathbf {X}) = {\ frac {1} {Z}} \ prod _ {f_ {j}} f_ {j} (x_ {j})} (согласно представлению факторного графа) можно рассматривать как меру внутренней энергии, присутствующей в системе, вычисляемой как E (X) = журнал ∏ fjfj (xj). {\ displaystyle E (\ mathbf {X}) = \ log \ prod _ {f_ {j}} f_ {j} (x_ {j}).} Тогда свободная энергия системы равна F = U - H = ∑ XP (X) E (X) + ∑ XP (X) журнал P (X). {\ Displaystyle F = UH = \ сумма _ {\ mathbf {X}} P (\ mathbf {X}) E (\ mathbf {X}) + \ sum _ {\ mathbf {X}} P (\ mathbf {X }) \ log P (\ mathbf {X}).} Затем можно показать, что точки сходимости алгоритма суммы-произведения представляют собой точки, в которых свободная энергия в такой системе минимизирована. Точно так же можно показать, что фиксированная точка итеративного алгоритма распространения убеждений в графах с циклами является стационарной точкой приближения свободной энергии. Распространение обобщенных убеждений (GBP) - распространение убеждений алгоритмы обычно представлены в виде уравнений обновления сообщений на факторном графе, включая сообщения между переменными узлами и их соседними факторными узлами, и наоборот. Рассмотрение сообщений между регионами в графе - это один из способов обобщения алгоритма распространения убеждений. Есть несколько способов определить набор регионов на графе, которые могут обмениваться сообщениями. Один метод использует идеи, представленные в физической литературе, и известен как Кикучи. Улучшения в производительности алгоритмов распространения убеждений также достигаются путем нарушения симметрии реплик в распределениях полей (сообщений). Это обобщение приводит к новому виду алгоритма, называемому (SP), который оказался очень эффективным в NP-полных задачах, таких как выполнимость и раскраска графа. . кластерный вариационный метод и алгоритмы распространения опроса - это два разных улучшения распространения убеждений. Имя (GSP) ожидает присвоения алгоритму, объединяющему оба обобщения. Распространение убеждений по Гауссу (GaBP) - распространение убеждений по Гауссу является вариантом алгоритма распространения убеждений, когда лежащие в основе распределения являются гауссовыми. Первой работой по анализу этой специальной модели была основополагающая работа Вейсса и Фримена. Алгоритм GaBP решает следующую проблему маргинализации: P (xi) = 1 Z ∫ j ≠ i exp (- 1 / 2 x TA x + b T x) dxj {\ displaystyle P (x_ {i}) = {\ frac {1} {Z}} \ int _ {j \ neq i} \ exp (-1 / 2x ^ { T} Ax + b ^ {T} x) \, dx_ {j}} где Z - константа нормализации, A - симметричная положительно определенная матрица (матрица обратной ковариации, также известная как матрица точности) и b - вектор сдвига. Аналогично, можно показать, что с использованием модели Гаусса решение проблемы маргинализации эквивалентно задаче назначения MAP : argmax x P (x) = 1 Z ехр (- 1/2 x TA x + b T x). {\ displaystyle {\ underset {x} {\ operatorname {argmax}}} \ P (x) = {\ frac {1} {Z}} \ exp (-1 / 2x ^ {T} Ax + b ^ {T } x).} Эта задача также эквивалентна следующей задаче минимизации квадратичной формы: min x 1/2 x TA x - b T x. {\ displaystyle {\ underset {x} {\ operatorname {min}}} \ 1 / 2x ^ {T} Ax-b ^ {T} x.} Что также эквивалентно линейной системе уравнений А х = b. {\ displaystyle Ax = b.} Сходимость алгоритма GaBP легче анализировать (по сравнению с общим случаем BP), и есть два известных достаточных условия сходимости. Первый был сформулирован Weiss et al. в 2000 году, когда информационная матрица A доминирует по диагонали. Второе условие сходимости сформулировано Johnson et al. в 2006 г., когда спектральный радиус матрицы ρ (I - | D - 1/2 A D - 1/2 |) < 1 {\displaystyle \rho (I-|D^{-1/2}AD^{-1/2}|)<1\,}, где D = diag (A). Позже Су и Ву установили необходимые и достаточные условия сходимости для синхронного GaBP и затухающего GaBP, а также другое достаточное условие сходимости для асинхронного GaBP. Для каждого случая условие сходимости включает проверку: 1) непустого набора (определяемого A); 2) спектрального радиуса определенной матрицы меньше единицы; 3) проблемы сингулярности (при преобразовании сообщения BP в убеждение) не встречается. Алгоритм GaBP был связан с областью линейной алгебры, и было показано, что алгоритм GaBP можно рассматривать как итерационный алгоритм для решения линейной системы уравнений Ax = b, где A - информационная матрица, а b - вектор сдвига. Эмпирически показано, что алгоритм GaBP сходится быстрее, чем классические итерационные методы, такие как метод Якоби, метод Гаусса – Зейделя, последовательная избыточная релаксация и другие. Кроме того, показано, что алгоритм GaBP невосприимчив к числовым проблемам предварительно обусловленного метода сопряженного градиента Синдромное декодирование АД -предыдущее описание алгоритма ВР называется декодированием на основе кодовых слов, который вычисляет приблизительную предельную вероятность P (x | X) {\ displaystyle P (x | X)} , учитывая полученное кодовое слово X {\ displaystyle X} . Существует эквивалентная форма, которая вычисляет P (e | s) {\ displaystyle P (e | s)} , где s {\ displaystyle s} - синдром полученного кодового слова X {\ displaystyle X} и e {\ displaystyle e} - декодированная ошибка. Декодированный входной вектор: x = X + e {\ displaystyle x = X + e} . Этот вариант изменяет только интерпретацию функции масс f a (X a) {\ displaystyle f_ {a} (X_ {a})} . Явно сообщения следующие:∀ xv ∈ D om (v), μ v → a (xv) = P (X v) ∏ a ∗ ∈ N (v) ∖ {a} μ a ∗ → v (xv). {\ Displaystyle \ forall x_ {v} \ in Dom (v), \; \ mu _ {v \ to a} (x_ {v}) = P (X_ {v}) \ prod _ {a ^ {*} \ in N (v) \ setminus \ {a \}} \ mu _ {a ^ {*} \ to v} (x_ {v}).} где P (X v) {\ displaystyle P (X_ {v})} - априорная вероятность ошибки для переменной v {\ displaystyle v} ∀ xv ∈ D om (v), μ a → v (xv) = ∑ xa ′: xv ′ = xv δ (синдром (xv ′) = s) ∏ v ∗ ∈ N (a) ∖ {v} μ v ∗ → a (xv ∗ ′). {\ displaystyle \ forall x_ {v} \ in Dom (v), \; \ mu _ {a \ to v} (x_ {v}) = \ sum _ {\ mathbf {x} '_ {a}: x '_ {v} = x_ {v}} \ delta ({\ text {синдром}} ({\ mathbf {x}}' _ {v}) = {\ mathbf {s}}) \ prod _ {v ^ {*} \ in N (a) \ setminus \ {v \}} \ mu _ {v ^ {*} \ to a} (x '_ {v ^ {*}}).} Этот синдром - декодер на основе не требует информации о полученных битах, поэтому может быть адаптирован к квантовым кодам, где единственной информацией является синдром измерения. В двоичном случае, xi ∈ {0, 1} {\ displaystyle x_ {i} \ in \ {0,1 \}} , эти сообщения могут быть упрощены вызвать экспоненциальное уменьшение 2 | {v} | + | N (v) | {\ displaystyle 2 ^ {| \ {v \} | + | N (v) |}}в сложностиОпределить логарифмическое отношение правдоподобия lv = log uv → a (xv = 0) uv → a (xv = 1) {\ displaystyle l_ {v} = \ log {\ frac {u_ {v \ to a} (x_ {v} = 0)} {u_ {v \ к a} (x_ {v} = 1)}}} , L a = log ua → v (xv = 0) ua → v (xv = 1) {\ displaystyle L_ {a} = \ log {\ frac {u_ {a \ to v} (x_ {v} = 0)} {u_ {a \ to v} (x_ {v} = 1)}}}, затемv → a: lv = lv (0) + ∑ a ∗ ∈ N (v) ∖ {a} (L a ∗) {\ displaystyle v \ to a: l_ {v} = l_ {v} ^ {(0)} + \ sum _ {a ^ {*} \ in N (v) \ setminus \ {a \}} (L_ {a ^ {*}})} a → v: L a = (- 1) sa 2 tanh - 1 ∏ v ∗ ∈ N (a) ∖ {v} tanh (lv ∗ / 2) {\ displaystyle a \ to v: L_ {a} = (- 1) ^ {s_ {a}} 2 \ tanh ^ {- 1} \ prod _ {v ^ {*} \ in N (a) \ setminus \ {v \}} \ tanh (l_ {v ^ {*}} / 2)} где lv (0) = журнал (P (xv = 0) / P (xv = 1)) = const {\ displaystyle l_ {v} ^ {(0)} = \ log (P (x_ {v} = 0) / P (x_ {v} = 1)) = {\ text {const}}} Апостериорное логарифмическое отношение правдоподобия можно оценить как lv = lv (0) + ∑ a ∈ N (v) (L a) {\ displayst yle l_ {v} = l_ {v} ^ {(0)} + \ sum _ {a \ in N (v)} (L_ {a})} Заключение Современные исследования в основном сосредоточены на создании LDPC-кодов с улучшенными характеристиками, а также методов их декодирования. Например, кодов на базе евклидовых геометрий. Для таких кодов также создаются и развиваются специальные методы декодирования и ускоренного декодирования с приемлемыми потерями в вероятности декодирования, и они показывают неплохие результаты. Дальнейшее развитие в рамках данной проблематики заключается в отработке современных алгоритмических решений в области кодирования и декодирования LDPC-кодов, а также в эмпирической проверке результатов современных теоретических исследований в этой области. Таким образом, при проектировании декодера необходимо учитывать множество факторов, чтобы добиться компромисса между различными параметрами, такими как скорость работы, энергопотребление, задержка, приближение к пределу Шеннона, порог ошибки, площадь кристалла (в случае ASIC) . Также важным является время и стоимость разработки и производства. Перспективными направлениями в исследовании декодеров в ближайшее время можно считать построение кодов, разработку архитектур и алгоритмов декодирования, а также многоскоростные и реконфигурируемые декодеры. Список используемой литературы D. MacKay and R. Neal, “Good codes based on very sparse matrices”, 1995 William E. Ryan, “An introduction to LDPC codes”, 2003 Sarah J. Johnson, “Iterative Error Correction”, 2010 Engling Yeo, BorivojeNikoli, and VenkatAnantharam, “Architectures and Implementations of Low-Density 2. Parity Check Decoding Algorithms”, 2002 TinooshMohsenin and Bevan Baas, “Trends and Challenges in LDPC Hardware Decoders”, 2009 S. Y. Chung, G. D. Forney, T. J. Richardson, R. Urbanke, “On the design of low-density parity-check codes within 0.0045dB of the Shannon limit”, 2001 T. J. Richardson, “Error Floors of LDPC Codes”, 2003 http://ru.wikipedia.org/wiki/LDPC http://www.mtdbest.ru/articles/obzor_dvoichnie_kodi_2.pdf Овчинников А. К вопросу о построении LDCP-кодов на основе евклидовых геометрий // Вопросы передачи и защиты информации: Сборник статей под ред. А. Крука. СПбГУАП. СПб., 2006. |