Реферат Теплопроводность газов, жидкостей и твёрдых тел Выполнили Студент 1 курса 1 группы Телипко Николай Валерьевич
 Скачать 76.83 Kb. Скачать 76.83 Kb.
|
|
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Факультет радиофизики и компьютерных технологий Реферат Теплопроводность газов, жидкостей и твёрдых тел Выполнили Студент 1 курса 1 группы Телипко Николай Валерьевич Преподаватель Прокопович Игорь Петрович Минск 2022 ОглавлениеВведение 3 Температурное поле[3] 4 Температурный градиент[5] 5 Тепловой поток[2] 7 Коэффициент теплопроводности[6] 8 Теплопроводность газов[7] 8 Теплопроводность жидкостей[9] 10 Теплопроводность твёрдых тел[2] 10 Дифференциальное уравнение теплопроводности[2][5] 12 Заключение 16 Список используемых источников 18 ВведениеВ природе и технике элементарные процессы распространения теплоты (теплопроводность, конвекция и тепловое излучение) очень часто происходят совместно. Теплопроводность представляет собой процесс распространения тепловой энергии при непосредственном соприкосновении отдельных частиц тела, имеющих различные температуры. Конвекция возможна только в текучей среде. Под конвекцией теплоты понимают процесс переноса тепловой энергии при перемещении объёмов жидкости или газа в пространстве из области с одной температурой в область с другой. При этом перенос теплоты неразрывно связан с переносом самой среды. Тепловое излучение – это процесс распространения тепловой энергии с помощью электромагнитных волн. При тепловом излучении происходит двойное превращение энергии: тепловая энергия излучаемого тела переходит в лучистую и обратно – лучистая энергия, поглощаясь телом, переходит в тепловую.[1] Теплопроводность в чистом виде большей частью имеет место лишь в твёрдых телах (материалах). Конвекция теплоты всегда сопровождается теплопроводностью, так как при движении жидкости или газа неизбежно соприкосновение отдельных частиц, имеющих различные температуры. Совместный процесс конвекции и теплопроводности называется конвективным теплообменом. В энергетике часто происходят процессы теплообмена между различными теплоносителями, разделёнными твёрдой поверхностью. Процесс передачи тепла от горячего теплоносителя (греющего) к холодному (нагреваемому) через разделяющую их стенку называется теплопередачей. Процесс теплопередачи осуществляется различными элементарными процессами теплопереноса, происходящими одновременно. В случае процесса теплообмена между поверхностью и газовым теплоносителем необходимо учитывать тепловое излучение.[4] Температурное поле[3]Явление теплопроводности в веществах представляет собой процесс распространения тепловой энергии при непосредственном Кулоновском (электромагнитном) взаимодействии отдельных частиц тела имеющих различные температуры (кинетические энергии). Теплопроводность обусловлена обменом энергией между микрочастицами вещества. При этом в газах перенос энергии осуществляется за счет диффузии молекул (атомов) и обмена между ними энергией при столкновениях. В жидкостях и диэлектриках тепловая энергия (энергия колебаний атомов) переносится при распространении упругих волн. В металлах перенос энергии в основном осуществляется путем обмена энергией между свободными электронами и передачи энергии от свободных электронов атомам решетки, роль упругих колебаний кристаллической решетки здесь имеет второстепенное значение. Аналитическая теория теплопроводности игнорирует молекулярное строение вещества и рассматривает вещество как сплошную среду. Такой подход правомерен, если размеры объектов исследования достаточно велики по сравнению с размерами молекул и расстоянием между ними. Следует отметить, что в жидкостях и газах чистая теплопроводность может быть реализована при выполнении условий, исключающих перенос тепла конвекцией. Всякое физическое явление в общем случае сопровождается изменением в пространстве и времени существенных для данного явления физических величин. Процесс теплопроводности, как и другие виды теплообмена, может иметь место только при условии, что в различных точках тела (или системы тел) температура неодинакова. В общем случае процесс передачи тепла теплопроводностью в твёрдом теле сопровождается изменением температуры, как в пространстве, так и во времени. Аналитическое исследование теплопроводности сводится к изучению пространственно-временного изменения температуры, т. е. к нахождению конкретного вида уравнения t = f (x, y, z, τ) (1.1) Уравнение (1.1) представляет собой математическое выражение температурного поля. Таким образом, температурное поле есть совокупность значений температуры во всех точках изучаемого пространства для каждого момента времени. Различают стационарное и нестационарное температурные поля. Уравнение (1.1) является записью наиболее общего вида температурного поля, когда температура изменяется с течением времени и от одной точки к другой. Такое поле отвечает неустановившемуся тепловому режиму теплопроводности и носит название нестационарного температурного поля. Если тепловой режим является установившимся, то температура в каждой точке поля с течением времени остается неизменной и такое температурное поле называется стационарным. В этом случае температура является функцией только координат: 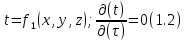 Температурное поле, соответствующее уравнениям (1.1) и (1.2), является пространственным, так как температура является функцией трёх координат. Если температура есть функция двух координат, то поле называется двухмерным: 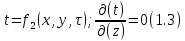 Если температура есть функция одной координаты, то поле называется одномерным: 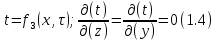 Температурный градиент[5]Если соединить точки тела, имеющие одинаковую температуру, можно получить поверхность равных температур, называемую изотермической. Итак, изотермической поверхностью называется геометрическое место точек в температурном поле, имеющих одинаковую температуру. Так как одна и та же точка тела не может одновременно иметь различные температуры, то изотермические поверхности не пересекаются. Они либо оканчиваются на поверхности тела, либо целиком располагаются внутри самого тела. Пересечение изотермических поверхностей плоскостью дает на этой плоскости семейство изотерм. Они обладают теми же свойствами, что и изотермические поверхности, т.е. не пересекаются, не обрываются внутри тела, оканчиваются на поверхности либо целиком располагаются внутри самого тела. На рис. 1.1 приведены изотермы, температуры которых отличаются на Δt. 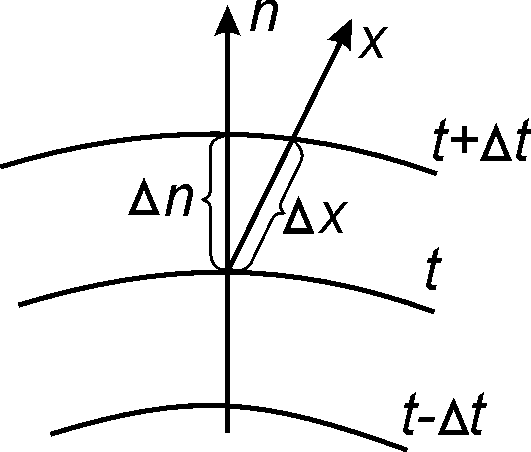 Рисунок 1.1 – Изотермические поверхности Температура в теле изменяется только в направлениях, пересекающих изотермические поверхности. При этом наибольший перепад температуры на единицу длины происходит в направлении нормали к изотермической поверхности.[5] Возрастание температуры в направлении нормали к изотермической поверхности характеризуется градиентом температуры. Градиент температуры есть вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры и численно равный производной от температуры по этому направлению, т. e. 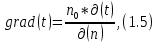 где n0 – единичный вектор, нормальный к изотермической поверхности и направленный в сторону возрастания температур; 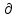 (t)/ (t)/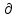 (n) – производная температуры по нормали n (n) – производная температуры по нормали nСкалярная величина температурного градиента 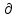 (t)/ (t)/ (n) не одинакова для различных точек изотермической поверхности. Она больше там, где расстояние Δn между изотермическими поверхностями меньше. (n) не одинакова для различных точек изотермической поверхности. Она больше там, где расстояние Δn между изотермическими поверхностями меньше.Величина  (t)/ (t)/ (n) в направлении убывания температуры (n) в направлении убывания температурыотрицательна. Проекции вектора grad(t) на координате оси Ох, Оу, Оz будут равны: 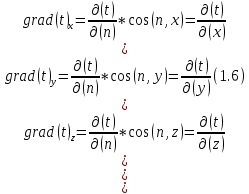 Тепловой поток[2]Необходимым условием распространения тепла в сплошной среде является неравномерность распределения температуры в рассматриваемой среде. Таким образом, для передачи энергии теплопроводностью необходимо неравенство нулю температурного градиента хотя бы в одной точке тела. Согласно гипотезе Фурье количество тепла d(Q)τ[Дж], проходящее через элемент изотермической поверхности d(F) за промежуток времени d(τ), пропорционально температурному градиенту 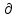 (t)/ (t)/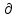 (n): (n):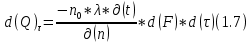 Опытным, путем установлено, что коэффициент пропорциональности в уравнении (1.7) есть физический параметр вещества. Он характеризует способность вещества проводить тепло и называется коэффициентом теплопроводности. Количество тепла, проходящее в единицу времени через единицу площади изотермической поверхности q=d(Q)τ/d(F)d(τ) [Вт/м2], называется плотностью теплового потока. Плотность теплового потока есть вектор, определяемый соотношением 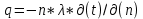 (1.8) (1.8)Вектор плотности теплового потока q направлен по нормали к изотермической поверхности. Его положительное направление совпадает с направлением убывания температуры, так как тепло всегда передается от более горячих частей тела к холодным.[5] Таким образом, векторы q и grad(t) лежат на одной прямой, но направлены в противоположные стороны. Это и объясняет наличие знака минус в правых частях уравнений (1.7) и (1.8). Скалярная величина вектора плотности теплового потока будет равна: 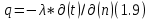 Многочисленные опыты подтвердили справедливость гипотезы Фурье, поэтому уравнение (1.8) является математической записью основного закона теплопроводности, который формулируется следующим образом: плотность теплового потока пропорциональна градиенту температуры. Количество тепла, проходящее в единицу времени через изотермическую поверхность F, называется тепловым потоком Q[Вт]. Если градиент температуры для различных точек изотермической поверхности различный, то количество тепла, которое пройдет через всю изотермическую поверхность в единицу времени, определяется как 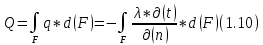 Где d(F) – элемент изотермической поверхности. Коэффициент теплопроводности[6]Как было сказано, коэффициент теплопроводности является физическим параметром вещества. В общем случае коэффициент теплопроводности зависит от температуры, давления и состояния вещества. В большинстве случаев коэффициент теплопроводности для различных материалов определяется опытным путем. Известен ряд методов экспериментального определения коэффициента теплопроводности.[7] Большинство из них основано на измерении теплового потока и градиента температур в заданном веществе. Коэффициент теплопроводности при этом определяется из соотношения 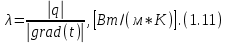 Из уравнения (1.11) следует, что коэффициент теплопроводности численно равен количеству тепла, которое проходит в единицу времени через единицу изотермической поверхности при температурном градиенте, равном единице. Так как тела могут иметь различную температуру, а при наличии теплообмена и в самом теле температура будет распределена неравномерно, то в первую очередь важно знать зависимость коэффициента теплопроводности от температуры. Опыты показывают, что для многих материалов с достаточной для практики точностью зависимость коэффициента теплопроводности от темпера- туры можно принять линейной 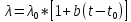 где λ0 – значение коэффициента теплопроводности при температуре t0; b– постоянная, определяемая опытным путем. Теплопроводность газов[7]Согласно кинетической теории вещества перенос тепла теплопроводностью в газах при обычных давлениях и температурах определяется переносом кинетической энергии молекулярного движения в результате хаотического движения и столкновения отдельных молекул газа. При этом коэффициент теплопроводности определяется соотношением  λ=1/ 3wlcv, (1.13) λ=1/ 3wlcv, (1.13)  где wˉ – средняя скорость перемещения молекул газа; lˉ – средняя длина свободного пробега молекул газа между их соударениями; сv – теплоёмкость газа при постоянном объёме; – плотность газа.  С увеличением давления в равной мере увеличивается и уменьшается lˉ , С увеличением давления в равной мере увеличивается и уменьшается lˉ , а произведение lˉ* сохраняется постоянным. Поэтому коэффициент теплопроводности мало изменяется в зависимости от давления. Исключение составляют очень маленькие (менее 2,67 кПа.) и очень большие (более 200 МПа) давления. а произведение lˉ* сохраняется постоянным. Поэтому коэффициент теплопроводности мало изменяется в зависимости от давления. Исключение составляют очень маленькие (менее 2,67 кПа.) и очень большие (более 200 МПа) давления.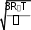 Средняя скорость перемещения молекул газа зависит от температуры Средняя скорость перемещения молекул газа зависит от температурыW= где Rµ – универсальная газовая постоянная, равная 8314,2 Дж/(К*кмоль); µ– молекулярная масса газа; Т – температура, К. Теплоёмкость газов возрастает с повышением температуры. Сказанным объясняется тот факт, что коэффициент теплопроводности для газов с повышением температуры возрастает. Коэффициент теплопроводности газов лежит в пределах значений от 0,006 до 0,6 Вт/(м*К). Среди газов своим высоким коэффициентом теплопроводности резко выделяются гелий и водород. Коэффициент теплопроводности у них в 5–10 раз больше, чем у других газов. Молекулы гелия и водорода обладают малой массой, следовательно, имеют большую среднюю скорость перемещения при одинаковом значении температуры, чем и объясняется их высокий коэффициент теплопроводности. Коэффициенты теплопроводности водяного пара и других реальных газов, существенно отличающихся от идеальных, сильно зависят также от давления. Для газовых смесей коэффициент теплопроводности не может быть определен по закону аддитивности, его нужно определять опытным путем. Теплопроводность жидкостей[9]Механизм распространения тепла в капельных жидкостях можно пред- ставить как перенос энергии путем нестройных упругих колебаний. Такое теоретическое представление о механизме передачи тепла в жидкостях, выдвинутое А.С. Предводителевым, было использовано Н.Б. Варгафтиком для описания опытных данных по теплопроводности различных жидкостей. Для большинства жидкостей теория нашла хорошее подтверждение. На основании этой теории была получена формула для коэффициента теплопроводности, имеющая следующий вид: 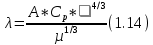 где ср – теплоёмкость жидкости при постоянном давлении; – плотность жидкости; µ – молекулярная масса. Коэффициент А, пропорциональный скорости распространения упругих волн в жидкости, не зависит от природы жидкости, но зависит от температуры; при этом произведение А*ср const. Так как плотность жидкости с повышением температуры убывает, то из уравнения (1.14) следует, что для жидкостей с постоянной молекулярной массой (неассоциированные или слабо ассоциированные жидкости) с повышением температуры коэффициент теплопроводности должен уменьшаться. Для жидкостей сильно ассоциированных (вода, спирт) в формулу (1.14) необходимо добавить коэффициент ассоциации, учитывающий изменение молекулярной массы. Коэффициент ассоциации также зависит от температуры, поэтому при разных температурах он может по-разному влиять на коэффициент теплопроводности жидкости.[5] Экспериментально показано, что для большинства жидкостей с повышением температуры коэффициент теплопроводности λ убывает, исключение составляют вода и глицерин. Коэффициент теплопроводности капельных жидкостей находится в пределах от 0,07 до 0,7 Вт/(м*К). При повышении давления коэффициенты теплопроводности жидкостей возрастают. Теплопроводность твёрдых тел[2]а) Металлы и сплавы. В металлах основным передатчиком тепла являются свободные электроны, которые можно уподобить идеальному одноатомному газу. Передача тепла при помощи колебательных движений атомов или в виде упругих звуковых волн не исключается, но ее доля незначительна по сравнению с переносом энергии электронным газом. Вследствие движения свободных электронов происходит выравнивание температуры во всех точках нагревающегося или охлаждающегося металла. Свободные электроны движутся как из областей, более нагретых, в области, менее нагретые, так и в обратном направлении. В первом случае они отдают энергию атомам, во втором отбирают. Так как в металлах носителями тепловой и электрической энергии являются электроны, то коэффициенты теплопроводности и электропроводности пропорциональны друг другу. При повышении температуры вследствие усиления колебательных движений атомов рассеивание электронов на них увеличивается. Это влечет за собой уменьшение коэффициентов тепло- и электропроводности чистых металлов. При наличии разного рода примесей коэффициент теплопроводности металлов резко убывает. Это можно объяснить увеличением структурных неоднородностей, которые приводят к рассеиванию электронов. Так, например, для чистой меди λ = 396 Вт/(м*К), а для меди со следами мышьяка λ = 142 Вт/(м*К).[6] В отличие от чистых металлов коэффициенты теплопроводности сплавов при повышении температуры увеличиваются. б) Твёрдые тела – диэлектрики (неметаллы). В диэлектриках с повышением температуры коэффициент теплопроводности обычно увеличивается. Как правило, для материалов с большей объемной плотностью коэффициент теплопроводности имеет более высокое значение. Он зависит также от структуры материала, его пористости и влажности. Многие теплоизоляционные и строительные материалы имеют пористое строение (пеноплекс, пенопласт, кирпич, бетон, асбест и др.), и применение закона Фурье к таким телам является в известной мере условным. Наличие пор в материале не позволяет рассматривать такие тела как сплошную среду. Условной является также величина коэффициента теплопроводности пористого материала. Эта величина имеет смысл коэффициента теплопроводности некоторого однородного тела, через которое при одинаковых форме, размерах и температурах на границах проходит то же количество тепла, что и через данное пористое тело. Коэффициент теплопроводности порошкообразных и пористых тел сильно зависит от их плотности. Например, при возрастании плотности от 400 до 800 кг/м3 коэффициент теплопроводности λ асбеста увеличивается от 0,105 до 0,248 Вт/(м*К).[6] Такое влияние на коэффициент теплопроводности объясняется тем, что λ воздуха заполняющего поры значительно меньше, чем λ твёрдых компонентов пористого материала. Эффективный коэффициент теплопроводности пористых материалов сильно зависит также от влажности. Для влажного материала коэффициент теплопроводности значительно больше, чем для сухого материала и воды в отдельности. Например, для сухого кирпича λ = 0,35 Вт/(м*К), для воды λ = 0,6 Вт/(м*К), а для влажного кирпича λ = 1,0 Вт/(м*К). Этот эффект может быть объяснен конвективным переносом тепла, возникающим благодаря капиллярному движению воды внутри пористого материала, и частично тем, что абсорбционно связанная влага имеет другие характеристики по сравнению со свободной водой. Увеличение коэффициента теплопроводности зернистых материалов с изменением температуры можно объяснить тем, что с повышением температуры возрастает теплопроводность среды, заполняющей промежутки между зернами, а также увеличивается теплопередача излучением внутри зернистого массива. Коэффициенты теплопроводности строительных и теплоизоляционных материалов имеют значения, лежащие в пределах от 0,023 до 2,9 Вт/(м*К).[6] Материалы с коэффициентом теплопроводности ниже 0,25 Вт/(м*К), обычно применяют для тепловой изоляции конструкций и называются теплоизоляционными.[1] Дифференциальное уравнение теплопроводности[2][5]Изучение любого физического явления сводится к установлению зависимости между параметрами, характеризующими это явление. Для сложных физических процессов, в которых определяющие параметры могут существенно изменяться в пространстве и времени, установить зависимость между этими параметрами очень трудно. В этих случаях используют метод математической физики, который ограничивает промежуток времени и из всего пространства рассматривается элементарный объём. Это позволяет в пределах элементарного объёма и выбранного малого промежутка времени пренебречь изменением некоторых параметров, характеризующих процесс, и существенно упростить зависимость. Рассмотрим элемент массы, мгновенно занимающий объём d(x)d(y)d(z) с центром в точке x, y, z за элементарный промежуток времени d(τ) (см. рис. 1.1). b) 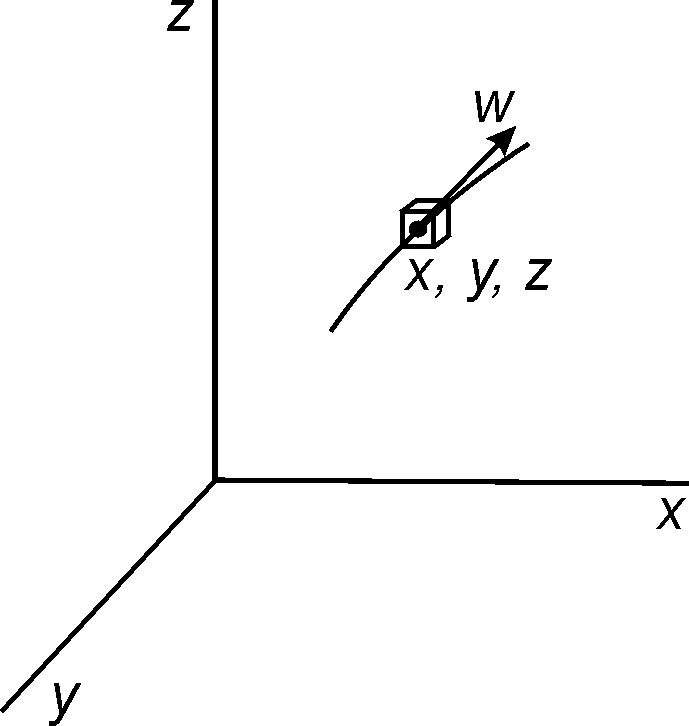 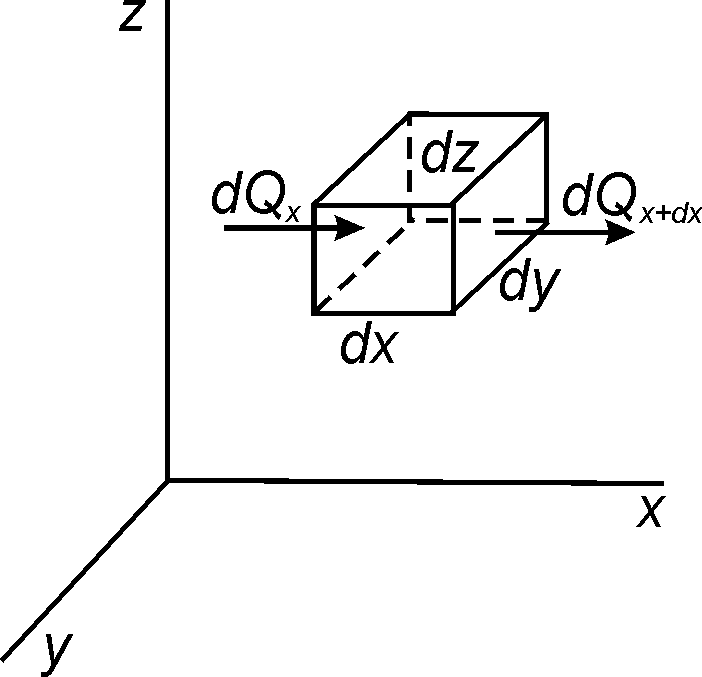 а) Расположение элемента объема в пространстве b) Элемент объема d(x)d(y)d(z) Рисунок 1.2 – К выводу уравнения теплопроводности[5] Для облегчения вывода дифференциального уравнения сделаем следующие допущения: тело однородно и изотропно; физические параметры постоянны; деформация рассматриваемого объема, связанная с изменением температуры, является очень малой величиной по сравнению с самим объемом; макроскопические частицы тела неподвижны друг относительно друга; внутренние источники тепла в теле, которые в общем случае могут быть заданы как q0 = f ( x, y, z, τ), распределены равномерно. В основу вывода дифференциального уравнения теплопроводности положен закон сохранения энергии, который в рассматриваемом случае может быть сформулирован следующим образом[2]: количество тепла d(Q), введенное в элементарный объем извне за время d(τ) вследствие теплопроводности, а также от внутренних источников, равно изменению внутренней энергии вещества, содержащегося в элементарном объеме: D(Q1) + d(Q2) = d(Q) , (1.15) где d(Q1) – количество тепла, введенное в элементарный объем путем теплопроводности за время d(τ); d(Q2) – количество тепла, которое за время d(τ) выделилось в элементарном объеме d(V) за счет внутренних источников; d(Q) – изменение внутренней энергии вещества, содержащегося в элементарном объеме d(V), за время d(τ). Для нахождения составляющих уравнения (1.15) выделим в теле элементарный параллелепипед со сторонами d(х), d(у), d(z) (см. рис. 1.2b). Параллелепипед расположим так, чтобы его грани были параллельны соответствующим координатным плоскостям. Количество тепла, которое подводится к граням элементарного объема за время d(τ) в направлении осей Ох, Оу, Оz, обозначим d(Qx), d(Qy), d(Qz), соответственно. Количество тепла, которое будет отводиться через противоположные грани в тех же направлениях, обозначим соответственно d(Qx+d(x)), d(Qy+d(y)), d(Qz+d(z)). Количество тепла, подведенное к грани d(y)d(z) в направлении оси ох за время d(τ), составляет d(Qx) = qx+d(y) *d(y)d(z)d(τ) , где qх – проекция плотности теплового потока на направление нормали к указанной грани. Количество тепла, отведенного через противоположную грань элементарного параллелепипеда в направлении оси Ох, запишется как dQx1+d(x) =qx+dx *d(y)d(z)d(τ) . Разница количеств тепла, подведенных к элементарному параллелепипеду и отведенных от него за время d(τ) в направлении оси ох представляет собой количество тепла d(Qx1): d(Qx1 )= d(Qx )- d(Qx+dx) . (1.16) Функция qх+d(x) является непрерывной в рассматриваемом интервале d(х) и может быть разложена в ряд Тейлора: 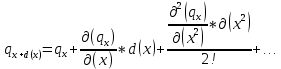 Если ограничиться двумя первыми членами ряда, то уравнение (1.16) за- пишется в следующем вид 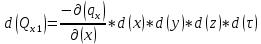 (1.17) (1.17)Аналогичным образом можно найти количество тепла, подводимое к элементарному объему и в направлениях двух других координатных осей Оу и Оz. Количество тепла d(Q1), подведенное теплопроводностью к рассматриваемому объему, будет равно 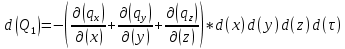 Определим вторую составляющую уравнения (1.15) d(Q2). Обозначим удельную производительность внутренних источников тепла через qv, [Вт/м3]. Удельную производительность внутренних источников называют также «объемной плотностью тепловыделения».[4] Объемная плотность – это количество тепла, которое выделяется в единице объема вещества в единицу времени. Тогда dQ2 = qv*d(V)*d(τ) . (1.19) Третья составляющая уравнения (1.20), характеризующая изменение внутренней энергии, может быть найдена по известному уравнению  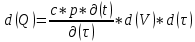 (1.20) (1.20)Подставляя полученные выражения (1.18), (1.19) и (1.20) в уравнение (1.15), получаем: 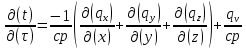 (1.21) (1.21)Проекции вектора плотности теплового потока на координатные оси Ох, Оу, Оz определяются выражениями (закон Фурье) 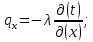 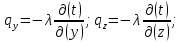 Подставляя полученные выражения проекций вектора плотности теплового потока в уравнение (1.26), получаем: 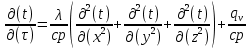 (1.22) (1.22)Если в уравнении (1.22) обозначит 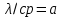 и 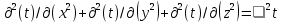 Где а – коэффициент температуропроводности, м2/с; 2t– оператор Лапласа в декартовой системе координат, то получим уравнение теплопроводности в общем виде 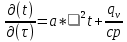 (1.23) (1.23)Выражение 2t в цилиндрической системе координат имеет вид: 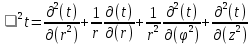 где r – радиальная, φ – угловая и z – аксиальная (осевая) координаты, соответственно. Выражение 2t в сферических координатах имеет вид: 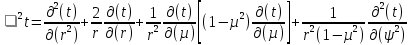 Где µ=cos(θ), θ и ψ – угловые координаты. Уравнение (1.23) называется дифференциальным уравнением теплопроводности. Оно устанавливает связь между временным и пространственным изменением температуры в любой точке тела, в котором происходит процесс теплопроводности. Коэффициент температуропроводности а является физическим параметром вещества, используется при описании нестационарных тепловых процессов и характеризует скорость изменения температуры. Если коэффициент теплопроводности характеризует способность тел проводить тепло, то коэффициент температуропроводности является мерой теплоинерционных свойств тела. Из уравнения (1.22) следует, что изменение температуры во времени 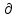 (t)/ (t)/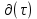 для любой точки пространства пропорционально величине а. Иначе говоря, скорость изменения температуры в любой точке тела будет тем больше, чем больше коэффициент температуропроводности а. Поэтому, при прочих равных условиях, выравнивание температур во всех точках пространства будет происходить быстрее в том теле, которое характеризуется большим коэффициентом температуропроводности. Величина коэффициента температуропроводности зависит от природы вещества. Например, жидкости и газы обладают большой тепловой инерционностью и, следовательно, малым коэффициентом температуропроводности. Металлы обладают малой тепловой инерционностью, так как они имеют большой коэффициент температуропроводности.[4] для любой точки пространства пропорционально величине а. Иначе говоря, скорость изменения температуры в любой точке тела будет тем больше, чем больше коэффициент температуропроводности а. Поэтому, при прочих равных условиях, выравнивание температур во всех точках пространства будет происходить быстрее в том теле, которое характеризуется большим коэффициентом температуропроводности. Величина коэффициента температуропроводности зависит от природы вещества. Например, жидкости и газы обладают большой тепловой инерционностью и, следовательно, малым коэффициентом температуропроводности. Металлы обладают малой тепловой инерционностью, так как они имеют большой коэффициент температуропроводности.[4]Заключение В своей работе я рассматривал теплопроводность жидкостей, газов и твердых тел. В общем случае я выяснил, что коэффициент теплопроводности λ для некоторых газов, жидкостей и твёрдых тел при атмосферном давлении, зависит от агрегатного состояния вещества, его атомно-молекулярного строения, температуры и давления, состава (в случае смеси или раствора). Если подробно рассматривать λ газа и жидкости, то, как и для газа, так и для жидкостей было сделано много различных опытов, впоследствии которых были получены формулы для определения λ. Для различных газов, будь он, идеальный газ или реальный газ или ещё какой-то в конечном итоге видно что если к примеру взять газ идеальный, состоящий из твёрдых сферических молекул диаметром d, согласно кинетической теории газов, была получена конкретная формула для определения λ, если взять реальный газ, то λ довольно сложная функция температуры и давления, причём с ростом Т и P значение λ возрастает, это я рассмотрел как пример для идеального и реального газа, (существуют газовые смеси, газ, состоящий из многоатомных молекул, для определения λ надо воспользоваться внутренними степенями свободы молекул, и другие примеры газов) Теперь переду к теплопроводности жидкостей, как я уже говорил, было тоже сделано множество опытов и получено, благодаря опытных данных, формулы для определения λ.Так вот в исследование посвященном теплопроводности жидкостей, можно увидеть три основных направления: 1.Вычисление кинетических коэффициентов средствами статистической физики; 2. Использование моделей теплового движения и механизмов переноса; 3. Полуэмпирический подход. В общем случае в твердых телах имеют место два основных механизма теплопроводности: свободными электронами (электронная теплопроводность λe) и атомными колебаниями (фононная или решеточная теплопроводность λp). Фононная теплопроводность характерна для диэлектриков, а электронная преобладает в металлах. Список используемых источников Техническая термодинамика и теплопередача: Научно-популярный, физика / Нащокин В. В. – М.: Книга по Требованию, 2013. – 496 с. Кикоин А.К., Кикоин И.К. Общий курс физики. Молекулярная физика. Издание второе, переработанное - М.: 1976. - 480 с. Миснар А. Теплопроводность твердых тел, жидкостей, газов и их композиций. 1968 г. Исаченко В. П., Осипова В. А., Сукомел А. С. Теплопередача, изд.: Энергия, 1975 г. – 416 с. Теплопроводность материалов: учебное пособие / А.Г. Коротких;Томский политехнический университет. – Томск: Изд-во Томского политехнического университета, 2011. – 97 с. Лыков А.В. Тепломассообмен: справочник. – М.: Энергия, 1978. – 480 с. Цедерберг Н.В. Теплопроводность газов и жидкостей. – Л.: Госэнергоиздат, 1963. – 470 с. Филиппов Л.П. Исследование теплопроводности жидкостей. – М.: Изд-во МГУ, 1970. – 240 с. Шашков А.Г., Волохов Г.М., Абраменко Т.Н., Козлов В.П. Методы определения теплопроводности и температуропроводности. М.: Энергия, 1973. – 336 с. |
