Рефлексия как этап современного урока математики в условиях реализации фгос ооо
 Скачать 81.95 Kb. Скачать 81.95 Kb.
|
|
УДК 372.851 РЕФЛЕКСИЯ КАК ЭТАП СОВРЕМЕННОГО УРОКА МАТЕМАТИКИ В УСЛОВИЯХ РЕАЛИЗАЦИИ ФГОС ООО © Е. О. Барышева 1учитель математики, lisab2000@yandex.ru, МБОУ «СОШ №62», г. Курск, Россия В статье рассматривается понятие «рефлексия» и ее значение в процессе обучения. Описываются различные методы организации рефлексивной деятельности на уроках математики. Приводятся различные виды рефлексивных задач, используемых в процессе формирования математических понятий. Ключевые слова: рефлексия, математическое понятие, рефлексивная деятельность, рефлексивные задачи. Задачей учителя в учебном процессе является не только донести знания до ученика, привлечь внимание к изучению своего предмета, но и научить ребенка ставить цели, разрабатывать алгоритм достижения этих целей, а затем анализировать результаты своих действий и поступков. Рассматривая примерную структуру каждого типа урока по ФГОС, можно увидеть, что обязательным условием создания развивающей среды и формирования регулятивных УУД на уроке является этап рефлексии [5]. В данной статье мы приводим примеры из опыта организации рефлексивной деятельности на уроках математики, которые оказались наиболее удачными и способствовали самоанализу учащимися собственной деятельности. Практика показывает, что как начинающие учителя, так и учителя со стажем недостаточно придают значения такому этапу урока как рефлексия. Очень часто этот этап присутствует в структуре урока, но проектируется он формально. На наш взгляд, на организацию рефлексивной деятельности надо смотреть шире. Кроме того, рефлексия не обязательна должна проводиться в конце урока. Так что же такое «рефлексия»? Залогом успешного изучения математики является осознание приемов и средств, при помощи которых происходит учебная деятельность, умения верно оценивать свои достижения и возможности, совершать нужные выводы относительно собственного совершенствования. Рефлексия – это один из механизмов, дающий возможность добиться этих целей [1]. Рефлексия трактуется как форма активного личностного переосмысления человеком тех или иных содержаний своего индивидуального сознания, необходимых для успешного осуществления деятельности [4]. Рефлексия на уроке – это совместная деятельность учащихся и учителя, позволяющая улучшить учебный процесс, ориентируясь на личность и успехи каждого ученика. Рефлексия помогает учителю контролировать класс, в процессе проведения урока видеть, что учащиеся уже усвоили, а что требует дальнейшей совместной работы, то есть, «держать руку на пульсе». При этом важно также анализировать не только результаты своей работы, но и каждый прошедший этап урока, спрашивать себя: «Почему этот этап урока прошел более успешно, а другой – менее успешно?» и т.д. Одной из ключевых задач при обучении математике является задача формирования математических понятий. Правильная организация рефлексивной деятельности позволяет решать указанную задачу более эффективно. Далее мы рассмотрим ряд примеров организации такой рефлексивной деятельности при обучении геометрии. Практика показывает высокую эффективность использования на уроках математики лабораторных работ, в процессе выполнения которых учащиеся самостоятельно формулируют новые понятия и определяют их свойства. В ходе выполнения лабораторной работы учитель организует взаимопроверку учащихся, обсуждение итогов выполнения заданий, тем самым вовлекая учащихся в рефлексивную деятельность. В процессе обсуждения уточняются существенные признаки понятия, структура определения и его формулировка, проводятся контрпримеры к ошибочным определениям. Например, при введении понятия «трапеция» учащимся может быть предложена лабораторная работа следующего содержания. Например, при введении понятия «трапеция» учащимся может быть предложена лабораторная работа следующего содержания. Начертите параллельные прямые l и m. Проведите прямую n таким, чтобы она пересекла прямые l и m. Проведите прямую р, пересекающую прямые l и m и не параллельную прямой n. Обозначьте точки пересечения прямых A,В,С и D. Вы должны получить четырехугольник ABCD. Запишите: четырехугольник ABCD — трапеция. остановите основные существенные признаки понятия «трапеция». Попытайтесь сформулировать определение трапеции. Установите, является ли объект, изображённые в таблице 1 трапецией? Запишите в ячейки таблицы ответы «да» или «нет». Таблица – Изучение трапеции
В процессе выполнения задания № 8 лабораторной работы целесообразно стимулировать рефлексивную деятельность учащихся при помощи следующих вопросов и заданий: 8.1. Является ли объект под № 1 четырехугольником? 8.2. Какими признаками обладает объект под № 2? 8.3. Верно ли, что объект под № 3 является трапецией? Обоснуйте ответ. 8.4. Какой признак трапеции отсутствует у объекта под № 4? Главным структурным элементом рефлексии в процессе формирования математических понятий является рефлексивная задача. Под рефлексивными будем понимать задачи, способствующие формированию у учащихся умений осмысливать, и контролировать мыслительную деятельность, осуществлять поиск оснований собственных действий [2], [3]. При составлении рефлексивных задач к обычным задачам добавляются вопросы рефлексивной направленности, способствующие осознанию процесса ее решения. К рефлексивным мы также относим задачи, в которых выделена некоторая ситуация, требующая рефлексивного отношения. Нами были выделены следующие типы рефлексивных задач, которые могут способствовать усвоению математических понятий: Назовите существенные признаки понятия. Сформулируйте определение понятия. Проверьте, все ли существенные признаки вы указали в определении.Задача способствует осмыслению учащимися текста определения, усвоению и осознанию существенных признаков понятия, входящих в определение. Пример. Назовите существенные признаки понятия «вписанный угол». Сформулируйте определение. Проверьте, все ли существенные признаки вы указали в определении. Установите, относится ли предложенный объект к данному понятию. Обоснуйте ответ.Задача способствует проверке усвоения существенных признаков понятия и сформированности умения подводить объект под понятие. Пример.Установите, является ли объект, изображённый на рисунке 1, вписанным углом? Обоснуйте ответ. кажите признаки, которыми обладает вписанный угол. 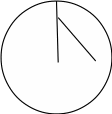 Рисунок 1 Достройте объект так, чтобы его можно было отнести к данному понятию. Задача способствует осознанию существенных признаков понятия, проверке сформированности наглядных образов, формированию умении применять свойства понятия. Пример. На рисунке 2 заданы три точки A, В, С. Определите местоположение четвертой точки D так, чтобы точки А, В, С и D были вершинами параллелограмма. Сколько решений имеет задача? Какие теоретические сведения вы использовали при ее решении? 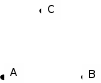 Рисунок 2 При решении данной задачи учащиеся должны получить три возможных случая построение параллелограмма (см. рисунок 3). 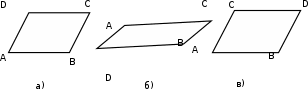 Рисунок 3 Приведите комментарии к решению задачи. Предложите другую последовательность действий в решении.Задача способствует осознанию действий, выполняемых в процессе решения, формированию умения осуществлять альтернативный подход. Пример. На рисунке 4 угол 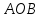 равен равен 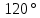 .Определите градусные меры углов .Определите градусные меры углов 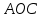 , , 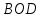 и и 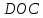 . К задаче приведено решение: . К задаче приведено решение:1) 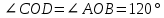 ; ;2) 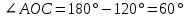 ; ;3) 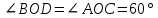 . .Приведите комментарии к решению. Предложите другую последовательность действий в решении задачи. 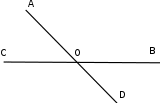 Рисунок 4 Найдите ошибки в предложенном решении. Задача способствует усвоению и осознанию способа решения, контролю действии в процессе решения задачи. Пример. Луч с делит угол ab, равный 150°, на два угла (см. рисунок 4). Найдите углы асn bс, если угол ас на 60° меньше угла bс. К задаче приведено такое решение: «Примем величину 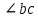 за х, тогда величина за х, тогда величина 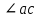 будет равна будет равна 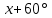 . Составим уравнение: . Составим уравнение: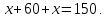 Решая уравнение, получим 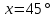 . Следовательно, . Следовательно, 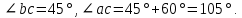 Ответ: 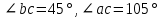 ». ».Какая ошибка была допущена в решении задачи? Исправьте ее. Подберите условия из списка, достаточные для того, чтобы объект относился к данному понятию.Задача способствует усвоению существенных признаков понятия, проверке сформированности умения подводить объект под понятие. Пример. Подберите условия из списка, достаточные для того, чтобы объект был биссектрисой треугольника по определению: а) отрезок биссектрисы угла треугольника; 6) луч; в) луч, исходящий из вершины треугольника; г) прямая, проходящая через вершину треугольника; д) соединяет вершину треугольника с точкой противоположной стороны; е) луч, делящий угол треугольника на два равных угла. Выберите из списка теоретические положения, которые следуют из того, что данный объект относится к данному понятию.Задача способствует проверке сформированности умения выводить следствия из факта принадлежности объекта объему данного понятия. Пример. Выберите из списка теоретические положения, которые следуют из того, что объект является медианой треугольника: а) отрезок; 6) прямая; в) линия; г) соединяет вершину треугольника с точкой противоположной стороны; д) соединяет вершину треугольника с серединой противоположной стороны; е) делит угол треугольника пополам; ж) делит сторону треугольника пополам; з) является высотой и биссектрисой треугольника. Составьте план решения задачи из набора предложений №1, затем из набора предложений №2 выберите те теоретические положения, которые входят в обоснование решения задачи. Данная задача способствует формированию осознанного применения теоретических сведения (определений, теорем, устанавливающих свойства понятие) при решении задач. Пример. На рисунке 5 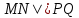 ; луч ; луч 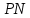 – биссектриса угла – биссектриса угла 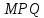 ; угол ; угол 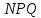 равен равен 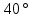 . Найдите величину угла . Найдите величину угла 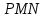 . Из набора а) — г) составьте план решения: . Из набора а) — г) составьте план решения:а) нахождение величины угла 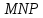 ; ;б) нахождение величины угла 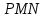 ; ;в) нахождение величины угла 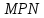 ; ;г) нахождение величины угла 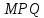 . .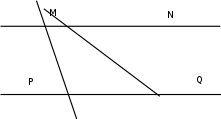 Рисунок 5 Из набора а) — ж) выберите те теоретические положения, которые входят в обоснование решения задачи (укажите их по порядку применения при решении задачи): определение параллельных прямых; признак параллельных прямых по накрест лежащим углам; свойство параллельных прямых по накрест лежащим углам; признак параллельных прямых по односторонним углам; свойство параллельных прямых об односторонних углах; свойство величин углов; определение биссектрисы угла. Приведем запись правильного ответа: план решения — в, г, б; обоснование решения — ж, е, д. Учащимся при формировании математических понятии целесообразно предлагать задания на исправление ошибок в формулировках определение понятий с использованием контрпримеров. Такие задания способствуют осознанному усвоению определения понятия, его существенных признаков, например; «Исправьте ошибки в формулировке определения понятия, приведя контрпример: «параллелограмм — это многоугольник, у которого противоположные стороны попарно параллельны». Таким образом, к рефлексивным задачам относятся задачи: на нахождение ошибок в условии предложенной задачи, на дополнение условия, на нахождение лишних данных в условии, на самостоятельное составление задач, на нахождение других способов решения. В заключении отметим, что рефлексивные задачи должны быть диалогичными, учитель должен содействовать тому, чтобы школьник по-разному мог взглянуть на условие задачи, попытаться решить ее разными способами, оценить задачу и ее решение с разных точек зрения. Библиографический список [1] Анисимов, О. С. Методологическая культура педагогической деятельности и мышления. – М. : Экономика, 1991. – 416 с. [2] Далингер, В. А. Совершенствование процесса обучения математике на основе реализации внутрипредметных связей. – Омск : ОмИПКРО, 1993. – 323 с. [3] Котенко, В. В. Рефлексивная задача как средство повышения обучаемости школьников в процессе изучения базового курса информатики: дис. канд. пед. наук. – Омск : 2000. – 166 с. [4] Семенов, И. Н. Проблема предмета и метода психологического изучения рефлексии / И. Н. Семенов, С. Ю. Степанов // Исследование проблем психологии творчества. – М., 1983. – С. 154–181. [5] Формирование универсальных учебных действий в основной школе: от действия к мысли. Система заданий: пособия для учителя / под ред. Асмолова, А. Г. – М. : Просвещение, 2011. - 159 с.с | |||||||||||||||||||||||||||||||||




