Режа Моддий нутанинг

• Название: Режа Моддий нутанинг
• Дата: 13.04.2022
• Размер: 494.5 Kb.
• Имя файла: 8888888.doc
• Тип: Документы; #468619

Моддий нуқтанинг тебранма харакати
Режа:

1. 
   Моддий нуқтанинг эркин тебранма ҳаракаати.
   
2. 
   Эквивалент бикрликлар.
   
3. 
   Моддий нуқтанинг сўнувчи тебранма ҳаракати
   
4. 
   Моддий нуқтанинг мажбурий тебранма ҳаракати. Резонанс.
   
5. 
   Муҳит қаршилик кучи таъсиридаги тебранма ҳаракат.
   

Моддий нуқтанинг тебранма ҳаракати

Қишлоқ хўжалиги машиналарининг кенг миқёсда ишлатилиши,шунингдек турли транспорт ҳамда сув иншоотларининг барпо бўлиши уларнинг қисмларида ҳосил бўладиган тебранишларни чуқур ўрганишни талаб қилади.

Машина ва иншоот қисмларининг тебранма ҳаракатларини ўрганиш кўп ҳолларда моддий нуқта тебранма ҳаракатини ўрганишга келтирилади.

Моддий нуқтанинг тебранма ҳаракати деб шундай ҳаракатга айтиладики,бунда нуқта мувозанат ҳолатидан гоҳ бир томонга,гоҳ иккинчи томонга навбатма-навбат четланади.Демак, тебранма ҳаракат такрорланувчи ҳаракатдир.

Тебранма ҳаракатлар асосан уч турга бўлинади.

1. Эркин (гармоник) тебранма ҳаракат.

2. Сўнувчи тебранма ҳаракат.

3. Мажбурий тебранма ҳаракат.

Моддий нуқтанинг эркин тебранма ҳаракати

Фараз қилайлик,моддий нуқтага ҳамма вақт унинг мувозанат ҳолати томон йўналган куч таъсир қилсин ва мазкур нуқта тўғри чизиқли ҳаракатда бўлсин (131-расм).

Моддий нуқта координатасининг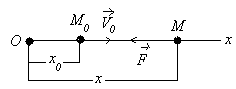



13.1-расм

функцияси сифатида ўзгарувчи ва мувозанат ҳолатига қараб йўналган куч қайтарувчи куч деб аталади. Қайтарувчи куч нуқтанинг ҳолатига боғлиқ бўлади,яъни:

F=-cx (13.1)

бунда c - моддий нуқтани узунлик бирлигига кўчириш учун зарур бўлган куч бўлиб,бикирлик коэффициенти дейилади, ўлчов бирлиги эса . x – нуқтанинг абциссаси.

Бошланғич пайтда М нуқтанинг абциссаси , тезлиги V₀ бўлсин.

М нуқтанинг ҳаракат дифференциал тенгламасини тузамиз:

(13.2)
бу ифодада белгилаш киритсак,у қуйидагича ёзилади: ( 13.3)

(13.4)

(13.4) нинг умумий ечими қуйидагича бўлади:

(13.5)

(13.5) даги C₁ ва C₂ ўзгармаслар бошланғич шартлардан фойдаланиб аниқланади:

(13.6)

Шундай қилиб, М нуқтанинг ҳаракати

(13.7)

тенглама билан аниқланади.

Моддий нуқта тебранма ҳаракатини умумий ҳолда текшириш қулай бўлиши учун ўрнига a ва ўзгармасларни қуйидагича танлаймиз:

(68.8)

(13.8) ни (13.5) га қўйиб, М нуқта ҳаракатини аниқловчи тенгламани қуйидаги кўринишга келтирамиз:

(68.9)

(13.8) ифодаларни аввал квадратга кўтариб қўшсак,сўнг (13.8) нинг иккинчисини биринчисига ҳадлаб бўлсак ва (13.6) ни эътиборга олсак,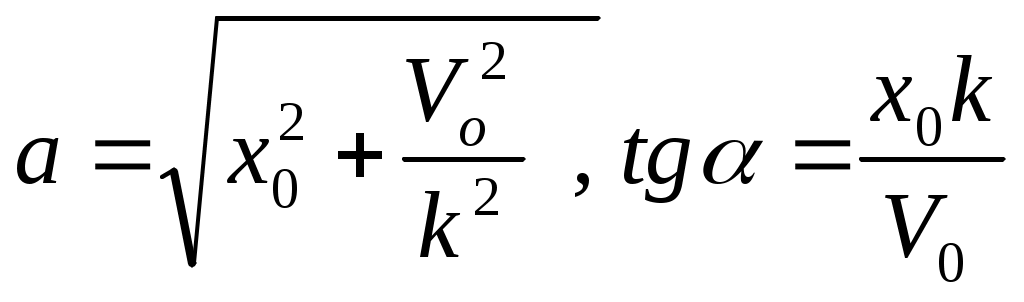

(13.10)

келиб чиқади.

(13.9) дан кўрамизки, моддий нуқтанинг қайтарувчи куч таъсиридаги ҳаракати даврий характерга эга бўлган эркин тебранма ҳаракатдан иборат экан.Шунинг учун (13.4) эркин тебранма ҳаракатнинг дифференциал тенгламаси дейилади. (13.9) тенглама моддий нуқтанинг эркин тебранма ҳаракат қонунини ифодалайди.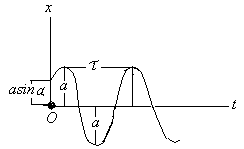

( 13.9) тенгламадаги a – нуқтанинг мувозанат ҳолатидан энг катта оғиши – тебраниш амплитудаси, kt+ - тебраниш фазаси, - бошланғич фаза, k – тебранишнинг доиравий такрорлиги дейилади.

Эркин тебранма ҳаракат графиги 13.2-расмда кўрсатилган. давр оралиғида тебраниш фазаси

га ўзгаришини ҳисобга олсак, (13.9) дан қуйидаги тенгламани ёзиш мумкин




132-расм
Бундан эркин тебранма ҳаракат даврини аниқловчи

(13.11)

формулани ҳосил қиламиз.

Тебраниш даврининг тескари қиймати тебраниш такрорлиги дейилади; уни билан белгиласак,таърифга кўра :



(13.10), (13.11) дан кўрамизки,тебраниш амплитудаси ва бошланғич фаза ҳаракатнинг бошланғич шартларига боғлиқ,тебраниш даври, шунингдек, тебраниш такрорлиги нуқтанинг бошланғич ҳолатига боғлиқ эмас экан. Бинобарин,тебраниш даври тебранма ҳаракатдаги нуқтанинг ўзгармайдиган характеристикасидир.Тебраниш даврини топиш учун тебранма ҳаракатнинг дифференциал тенгламасини (13.4) кўринишда тузиш ва k ни топиш кифоя.

Моддий нуқтанинг сўнувчи тебранма ҳаракати

Массаси m бўлган M моддий нуқта қайтарувчи куч ва муҳитнинг қаршилик кучи таъсирида тўғри чизиқли ҳаракатда бўлсин (13.3-расм).

Муҳитнинг қаршилик кучини моддий нуқта тезлигининг биринчи даражасига пропорционал дейлик: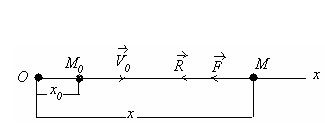



Бу ҳаракатни текшириш учун моддий нуқта ҳаракатининг дифференциал тенгламасини тузамиз:

13.3-рaсм

(13.12)

(13.12) ни қуйидаги кўринишда ёзамиз:

=0 (13.13)

(13.13) нинг икки томонини m га бўлиб, деб белгилаймиз. Натижада

(13.14)

келиб чиқади.

Бошланғич пайтда М нуқта М₀ да бўлиб, унинг абциссаси x₀ , тезлиги бўлсин. (13.14) нинг ечимини топиш учун характеристик тенглама тузамиз:



Бу тенглама ечими



кўринишда бўлиб, ундаги b вa k га нисбатан қуйидаги ҳоллар учраши мумкин:

1) k > b қаршилик кучи қайтарувчи кучга нисбатан кичик бўлган ҳол;

2) k < b қаршилик кучи қайтарувчи кучга нисбатан катта бўлган ҳол;

3) k = b –чегара ҳол.

Бу ҳолларни алоҳида-алоҳида текширамиз.

1).k > b бўлганда характеристик тенглама илдизлари комплекс сондан иборат,яъни:



ёки



бунда

Бу ҳолда (69.4) дифференциал тенгламанинг умумий ечими қуйидагича бўлади:

(13.15)

(13.15) даги C₁ , C₂ ўзгармасларни (13.8) кўринишда танлаб олсак, (13.15) қуйидагича ёзилади:

(13.16)

(13.16) даги a ифода вақт ўтиши билан нолга интилади,яъни ҳаракат аста-секин сўна боради. Шунинг учун муҳитнинг қаршилик кучи ва қайтарувчи куч таъсиридаги нуқтанинг ҳаракати кичик қаршиликлар ҳолда сўнувчи тебранма ҳаракат бўлади.

(13.14) сўнувчи тебранма ҳаракат дифференциал тенгламасини (13.15) ёки (13.16) сўнувчи тебранма ҳаракат қонунини ифодалайди.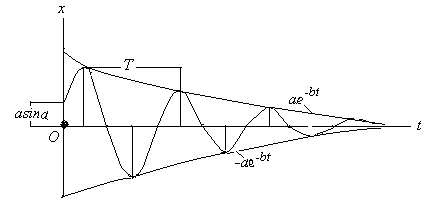



13.4-расм

Сўнувчи тебранишнинг графиги (13.16) тенгламага асосан, тенгламалари бўлган икки эгри чизиқ орасида бўлиб,бу эгри чизиқларга уриниб ўтади (13.4-расм).

(13.16) даги a ва ўзгармасларни ҳаракатнинг бошланғич шартларидан фойдаланиб топамиз.

(13.16) дан ҳосила оламиз:

(13.17)

(13.16) ва (13.16) га бошланғич шартларни қўйсак:



ёки

(13.16)

келиб чиқади.

(13.16) тенгламалар системасини ечсак:

(13.17)

ҳосил бўлади.

(13.14) тенгламада қатнашгани туфайли нуқта ҳаракати даврий характерга эга, лекин нуқтанинг тўлиқ аввалги ҳолатига қайта олмаслигини кўрсатади. Шунинг учун сўнувчи тебранишнинг тебраниш даври тушунчасини шартли киритамиз:

(13.18)

ёки

(13.19)

(13.19) даги ифодани қаторга ёйиб, b/k нинг иккинчи даражадан юқори бўлган даражадаги ҳадларини ташлаб юборсак ва (13.11) ни эътиборга олсак,

(13.20)

келиб чиқади.Бу ифодадаги b/k қаршилик коэффициенти деб аталади.

(13.20) дан кўрамизки, T > , бироқ қаршилик жуда кичик бўлганда тебранма ҳаракат даври эркин тебраниш давридан деярли фарқ қилмайди,яъни

Энди, сўнувчи тебранма ҳаракат амплитудасининг ўзгаришини кўриб чиқамиз. M нуқта ўзининг мувозанат ҳолатидан v - максимал оғишини , v+1 - максимал оғишини билан белгилаймиз. Бу оғишларга мос келган вақтлар вa учун (13.14) қуйидагича бўлади:





бундан

(13.21)

келиб чиқади. (13.21) дан кўрамизки нисбат ўзгармас ҳамда нолдан кичик.

Демак, тебраниш амплитудасининг ҳар бир T давр ўтишдаги кетма-кет қийматлари,махражи бўлган камаювчи геометрик прогрессияни ташкил қилади. - тебраниш декременти (сўниш фактори) дейилади.Тебраниш декрементидан олинган натурал логарифмнинг модули эса логарифмик декремент деб аталади ва қуйидагича ёзилади:

(13.22)

бу ерда b - сўниш коэффициенти.

2) k < b бўлган ҳолда характеристик тенглама илдизлари ҳақиқий ва манфий бўлади, яъни:



Натижада (13.11) дифференциал тенгламанинг умумий ечими қуйидагича ёзилади:

(13.23)

(13.23) дан кўрамизки, k < b ҳолда нуқта ҳаракати даврий характерга эга эмас. Шунинг учун бу ҳолдаги ҳаракат апериодик (яъни даврий бўлмаган) сўнувчи ҳаракат дейилади.

(13.23) даги C₁, C₂ ўзгармаслар ҳаракатнинг бошланғич шартларидан фойдаланиб аниқланади.

(13.23) дан вақт бўйича ҳосила оламиз:

(13.24)

(13.23) ва (69.16) га бошланғич шартларни қўйсак:

x₀ = C₁ + C₂, (13.25)

ҳосил бўлади.

(13.25) дан:

, (13.26)

келиб чиқади.

(13.26) ни (13.23) га қўйсак, М нуқтанинг берилган бошланғич шартларни қаноатлантирувчи апериодик ҳаракат тенгламаси ҳосил бўлади:

(13.27)

3) b = k да (13.4) дифференциал тенгламанинг умумий ечими қуйидагича бўлади:

(13.28)

Демак,бу ҳолда ҳам ҳаракат апериодик бўлади.

(13.28) дан ҳосила оламиз:

(13.29)

(13.28) ва (69.21) га бошланғич шартларни қўйсак:



ҳосил бўлади.Бу тенгликлардан



келиб чиқади.

Демак, k = b бўлган ҳолдаги апериодик ҳаракат тенгламаси қуйидагича бўлади:

(13.30)

Кейинги икки ҳолда моддий нуқта тебранма ҳаракат қилмай асимтотик равишда нолга яқинлашади.

1 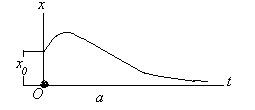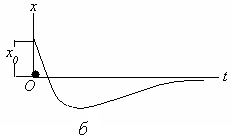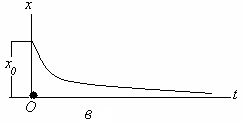35-рaсм

Бундай ҳаракатнинг графиги моддий нуқтанинг бошланғич ҳолатига ҳамда бошланғич тезликнинг модули ва йўналишига боғлиқ. 13.5-расмда турли бошланғич шартлар учун b > k ҳолдаги апериодик ҳаракат графиги кўрсатилган:

a) x₀ >0 ,V₀ >o; (13.5-рaсм,a) .

б) x₀ >0 ,V₀ >o лекин, ) , ) ; (135-расм,б)

в) лекин, , ; (135-расм,в)

b = k ҳолда ҳам апериодик сўнувчи ҳаракат графиги 13.5-расмда кўрсатилганига ўхшаш бўлади.
2.Моддий нуқтанинг мажбурий тебранма ҳаракати.

Моддий нуқта қайтарувчи куч ҳамда вақтнинг узлуксиз функцияси сифатида ўзгарувчи ва уйғотувчи куч деб аталувчи куч таъсирида тўғри чизиқли ҳаракатда бўлсин (136-расм).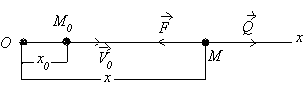



У
13.6-расм
йғотувчи куч гармоник қонун бўйича ўзгарсин яъни:

(13.2.1)

(13.2.1) да Q уйғотувчи кучнинг энг катта қиймати, p - доиравий такрорлиги, pt+ - фазаси, - бошланғич фазаси. Уйғотувчи куч даври эса га тенг.

Бошланғич пайтда M нуқта M₀ да бўлиб,унинг координатаси x_o, тезлиги V_o бўлсин.

Моддий нуқтанинг ҳаракат дифференциал тенгламасини тузамиз:

(13.2.2)

(13.2.2) ни қуйидаги кўринишда ёзиб оламиз:



белгилашлар киритсак,

(13.2.3)

ҳосил бўлади.

Дифференциал тенгламалар назариясидан маълумки, (13.2.3) дифференциал тенглама ечими қуйидагича ёзилади:

(13.2.4)

(13.2.4) да x₁ билан

(13.2.5)

бир жинсли дифференциал тенгламанинг умумий ечими белгиланган; эса (13.2.3) нинг хусусий ечимидан иборат.

(13.2.5) дифференциал тенгламанинг умумий ечими:

(13.2.6)

кўринишда ифодаланиши бизга маълум.

(13.2.3) ўзгармас коэффициентли чизиқли бир жинсли дифференциал тенгламанинг хусусий ечимини қуйидаги кўринишда оламиз:

(13.2.7)

(13.2.7) даги B коэффициентни аниқлаш учун (70.7) дан вақт бўйича иккинчи тартибли ҳосила оламиз:

(13.2.8)

(13.2.7) ва (13.2.8) ни (13.2.3) га қўямиз:



Б у айниятдан:

Натижада (13.2.7) тенглама қуйидагича ёзилади:

(13.2.9)

(13.2.9) тенглама билан аниқланувчи ҳаракат моддий нуқтанинг мажбурий тебранма ҳаракати дейилади.

Демак, (13.2.3) нинг умумий ечими қуйидагича ёзилади:

(13.2.10)

(13.2.10) даги a ва ҳаракатнинг бошланғич шартларидан фойдаланиб аниқланади.

(13.2.9) дан кўрамизки,мажбурий тебранма ҳаракат амплитудаси ёки нуқтанинг энг катта динамик силжиши:

(13.2.11)

бўлади.

(13.2.11) дан фойдаланиб, (13.2.9) ни қуйидаги кўринишларда ёзиш мумкин:

aгaр k > p бўлса;

ва агар k < p бўлса.

Бу муносабатларга биноан k > p бўлганда мажбурий тебраниш фазаси уйғотувчи куч фазаси билан бир хилда бўлади; k < p ҳолда эса мажбурий тебраниш фазаси уйғотувчи куч фазасидан га орқада қолади.

Мажбурий тебраниш амплитудаси билан p/k нисбат орасидаги боғланишни текширайлик. Бунинг учун (13.2.11) ни қуйидагича ёзамиз: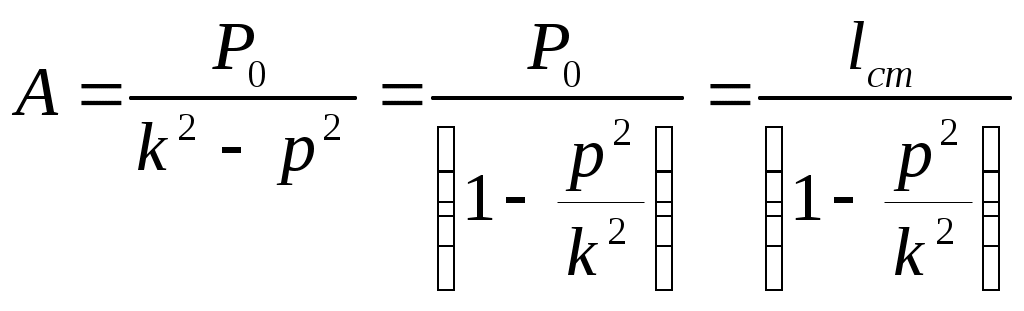

(13.2.12)

бунда билан моддий нуқтанинг уйғотувчи куч максимал қиймати таъсирида олган статик силжиши белгиланган.

(13.2.11) дан кўрамизки, мажбурий тебраниш амплитудаси уйғотувчи куч ҳамда эркин тебраниш доиравий такрорликларига боғлиқ.

М 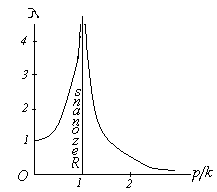оддий нуқта динамик силжишининг статик силжишига нисбати динамик коэффициент дейилади.

Уни билан белгилаймиз:

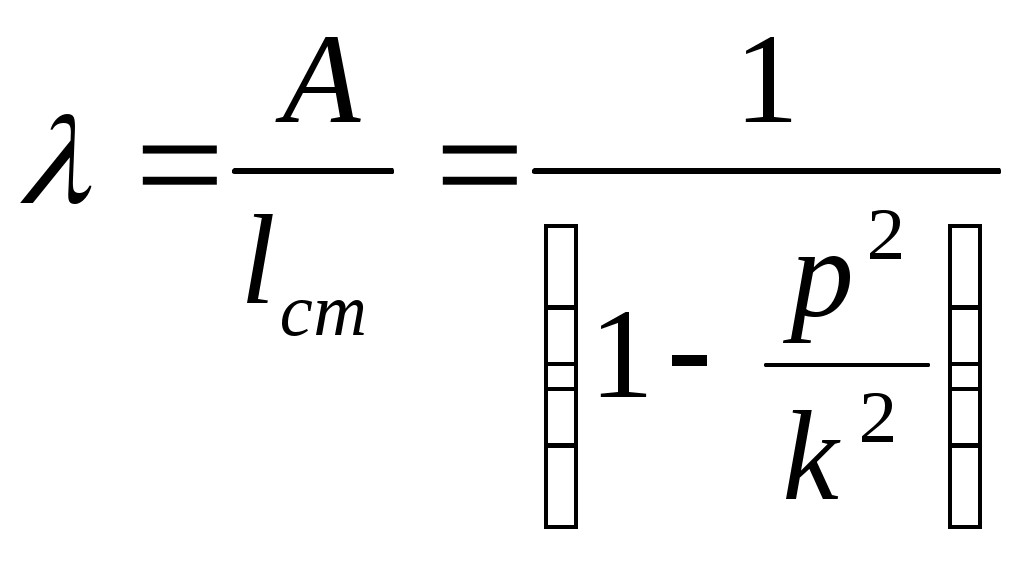(13.2.13)

Динамик коэффициент билан орасидаги (13.2.13) боғланиш графиги 13.7-расмда тасвирланган.

13.7-расм

Бошланғич шартлар , бўлган ҳолдаги ҳаракатни текшириш учун (13.2.3) дифференциал тенгламанинг умумий ечимини қуйидаги кўринишда ёзамиз:

(13.2.14)

(13.2.14) дан вақт бўйича ҳосила оламиз:

(13.2.15)

Моддий нуқта ҳаракатининг бошланғич шартларини (13.2.14) ва (13.2.15) га қўйсак: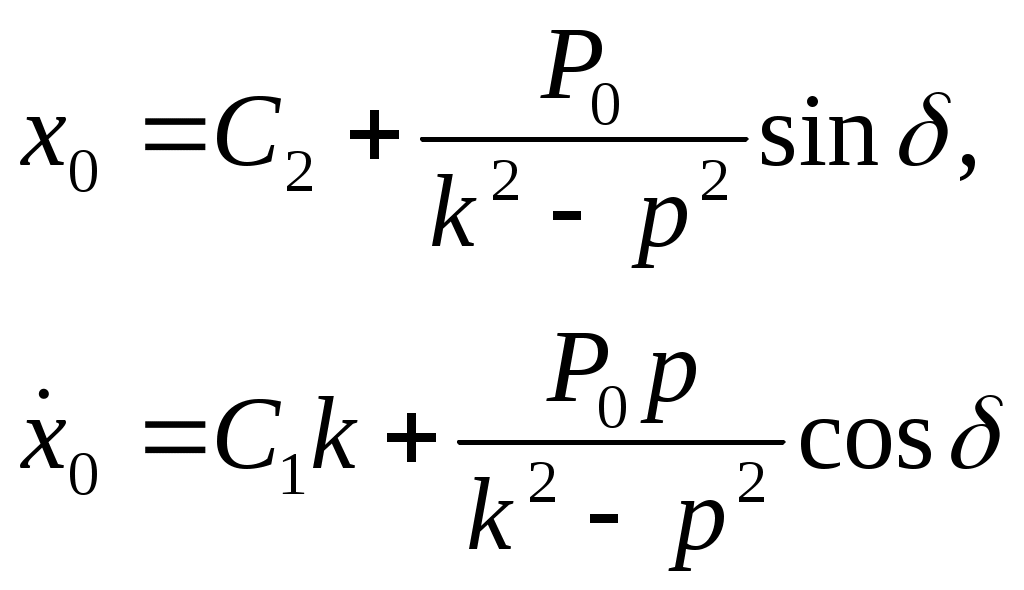

(13.2.16)

ҳосил бўлади.

(13.2.16) дан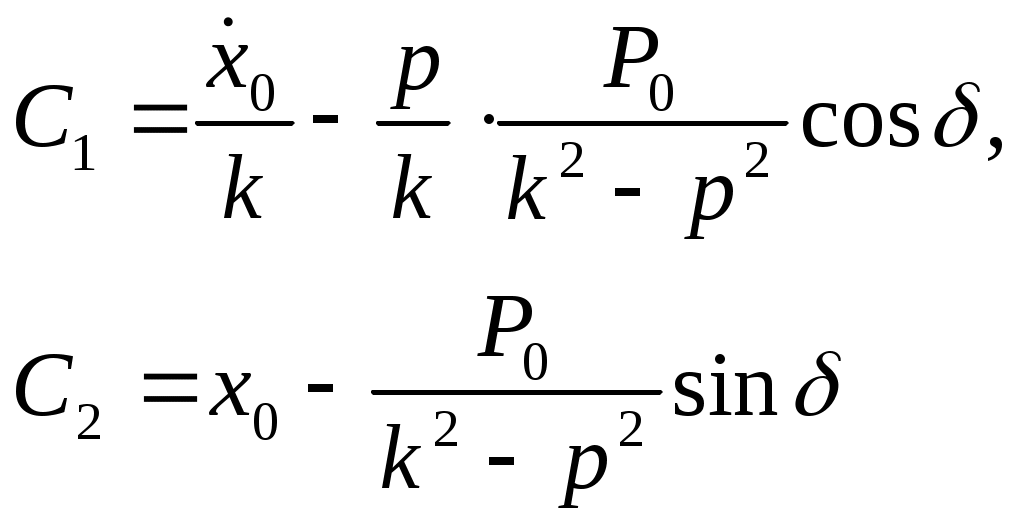



келиб чиқади. Демак, (13.2.14) қуйидагича ёзилади:

(13.2.17)

(13.2.16) дан кўрамизки, ҳамда бўлганда тебраниш ўзига хос кўринишга эга бўлади.Бу ҳол “тепиш” ҳоли дейилади.

“Тепиш” ҳолининг тенгламаси:



ёки

(13.2.18)

бўлади.

(13.2.18) тенглама билан ифодаланадиган ҳаракатнинг доиравий такрорлиги p,даври амплитудаси даврий функция сифатида ўзгарувчи тебранма ҳаракатдан иборат дейиш мумкин.Бу тебраниш амплитудаси:



Бу амплитуданинг даври



ва у T га нисбатан анча катта бўлади.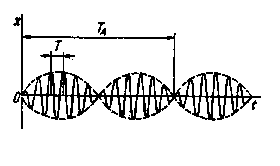

( 13.2.18) графиги 13.8-расмда кўрсатилган. Мажбурий ва эркин тебраниш доиравий такрорликлари бир хил бўлган (p=k) ҳол резонанс ҳоли деб аталади.

p=k бўлганда (13.2.3) дифференциал тенглама қуйидагича ёзилади:

(13.2.19)

Резонанс ҳолида (13.2.19) тенгламанинг хусусий ечимини қуйидаги кўринишда аниқлаймиз:

138-расм

(13.2.20)

(13.2.20) дан вақт бўйича ҳосила оламиз:

(13.2.21)

(13.2.20) ва (13.2.21) ни (13.2.19) га қўйсак:

) (13.2.22)

ҳосил бўлади. (13.2.22) дан:



келиб чиқади.

Демак, (13.2.19) дифференциал тенгламанинг умумий ечими қуйидагича бўлади:

(13.2.23)

(13.2.23) дан кўрамизки, нуқтанинг ҳаракати эркин ва мажбурий тебранишлар йиғиндисидан иборат.

Резонанс ҳолдаги мажбурий тебранма ҳаракат тенгламаси

(13.2.24)

бўлади.

(13.2.24) да 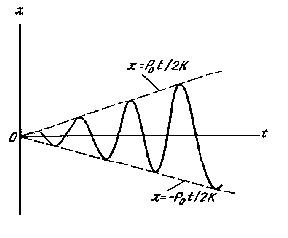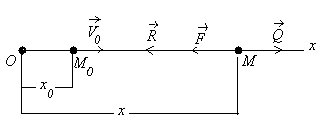мажбурий тебраниш амплитудаси, фазаси, эса доиравий такрорлигидан иборат. (13.2.24) га биноан, резонанс ҳолатидаги мажбурий тебраниш фазаси уйғотувчи куч фазасидан га орқада қолади, амплитуда эса вақтга пропорционал ўзгаради.





13.9-расм 14.0-расм

(13.2.24) тенглама билан аниқланувчи ҳаракат графиги 13.9-расмда тасвирланган.

3.Моддий нуқтанинг мажбурий тебранма ҳаракатига муҳит қаршилик кучининг таъсири

М моддий нуқта қайтарувчи, уйғотувчи кучлар ҳамда муҳитнинг қаршилик кучи таъсирида тўғри чизиқли ҳаракатда бўлсин. Бошланғич пайтда М нуқта М₀ да бўлиб, унинг абциссаси x₀ , тезлиги V₀ бўлсин ( 14.0-расм ).

Моддий нуқтанинг ҳаракати дифференциал тенгламасини тузамиз:

(13.3..1)

Б
унда

бўлгани учун (13.3.1) қуйидагича ёзилади:

(13.3.2)

Қуйидаги белгилашларни киритайлик:



У ҳолда (13.3.2) тенглама

(13.3.3)

кўринишни олади.

(13.3.3) тенглама муҳит қаршилик кучи таъсир этганда моддий нуқтанинг мажбурий тебранма ҳаракати дифференциал тенгламасидан иборат.

(13.3.3) тенгламанинг умумий ечими (10.4) тенглама умумий ечими билан (13.3.3) тенглама хусусий ечимининг йиғиндисидан иборат, яъни:



бу ерда x₁ b ва k ларнинг сон қийматларига қараб (10.6),(10.15) ёки (10.20) кўринишида бўлади, x₂ эса қуйидагича топилади:

(13.3.4)

D₁ ва D₂ ўзгармасларни аниқлаш учун (13.3.4) дан вақт бўйича биринчи ва иккинчи тартибли ҳосила оламиз:

(13.3.5)

(13.3.4) ва (13.3.5) ларни (13.3.3) га қўйсак:

(13.3.6)

ҳосил бўлади.

(13.3.6) дан: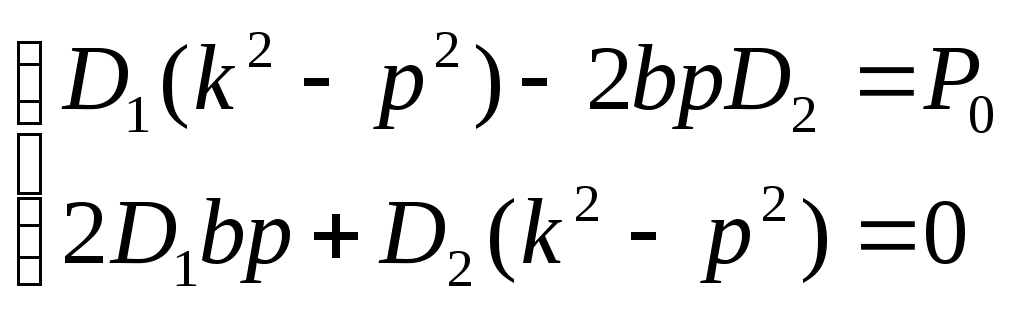

(13.3.7)

келиб чиқади.

(13.3.7) тенгламалар сиcтемасини ечсак:

(13.3.8)

Натижада (13.3.3) дифференциал тенгламанинг хусусий ечими қуйидаги кўринишда ёзилади:

(13.3.9)

Муҳит қаршилигидаги мажбурий тебранишни умумий ҳолда текшириш қулай бўлиши учун D₁ ва D₂ ўзгармаслар ўрнига А_қ ва ўзгармасларни киритамиз.Уларни қуйидагича танлаймиз:

D₁=А_қ , D₂=А_қ (13.3.10)

(13.3.10) ни аввал квадратга ошириб қўшсак,сўнгра (13.3.10) нинг иккинчисини биринчисига ҳадлаб бўлсак ва (13.3.8) эътиборга олсак:

А_қ (13.3.11)

(13.3.12)

келиб чиқади.

(13.3.10) ни (13.3.4) га қўямиз.У ҳолда

А_қ (13.3.13)

бўлади.

Шундай қилиб (13.3.3) дифференциал тенгламанинг умумий ечими

1) b
, (13.3.14)

2) b>k ҳолда

, (13.3.15)

3) b=k ҳолда

(1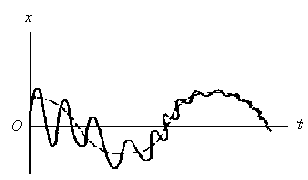3.3.16)

т енгламалар билан ифодаланади ва улардаги а , , ва ўзгармаслар ҳаракатнинг бошланғич шартларидан фойдаланиб аниқланади.

Муҳит қаршилик кучи таъсир этганда моддий нуқта тебранма ҳаракатининг графиги b
(13.3.14) , (13.3.15) ва (13.3.16) тенгламалардаги иккинчи ҳад,яъни:

14.1-рaсм (13.3.17)

муҳит қаршилик кучи ҳисобга олинган ҳолда моддий нуқтанинг мажбурий тебранма ҳаракатини ифодалайди.

Мажбурий тебраниш амплитудаси (13.3.11) тенгликдан аниқланади.