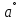Баллистическое движение. Дальность полёта. Баллистическое движение (7). Реждение средняя общеобразовательная школа 2 Баллистическое движение. Дальность полёта Бологов Дмитрий
 Скачать 312.85 Kb. Скачать 312.85 Kb.
|
|
Муниципальное автономное общеобразовательное учреждение средняя общеобразовательная школа №2 Баллистическое движение. Дальность полёта Выполнил: Бологов Дмитрий ученик 10 класса Г Руководитель: Перевалова Наталья Васильевна, учитель физики Научный консультант: Дмитрий Степанович Камаев, Преподаватель БФ ПНИПУ Г.Березники 2021г Введение Актуальность темы. 1.2 Проблема. 1.3 Объект исследования. 1.4 Предмет исследования. 1.5 Цель работы. 1.6 Задачи Методы исследования Основная часть. Анализ теоретического материала План эксперимента 1. Проведение эксперимента с игрушечным пистолетом 2. Описание программы Excel 3. Исследование зависимости l(a) и l(v) без сопротивления воздуха 4. Исследование зависимости l(a) и l(v) c учётом сопротивления воздуха 2.3 Проведение исследовательской по плану 1,2,3,4. 2.4 Результаты исследования 3. Вывод. 4. Заключение. 1.Введение Актуальность: Механика является наукой о движении, а движение охватывает все происходящее во Вселенной, начиная от простого перемещения и кончая мышлением. На всем протяжении истории науки механика была, есть и будет фундаментом физики, наиболее тесно связанной с окружающим нас миром. Механика является тем разделом физики, который благодаря строгости и логичности своего построения в сильной степени способствует развитию мышления учащихся. От его усвоения зависит успешность изучения всех разделов курса физики. В нашей жизни мы повсеместно сталкиваемся с баллистическим движением, когда бросаем различные тела или поливаем что-то. Баллистическое движение хорошо представлено в различных видах спорта, где взаимодействия людей связаны с мячом. Проблема: Улучшить освоение темы «Тело, брошенное под углом к горизонту» на примере исследования зависимости дальности полёта от начальной скорости и угла броска. Цель: Исследование баллистического движения с помощью программы Excel и физического эксперимента. Задачи: 1. Анализ теоретического материала 2. Исследовать баллистическое движения с помощью программы XL: установить зависимость дальности от начальной скорости и угла броска без учёта силы сопротивления воздуха и с учётом силы сопротивления. Построить и интерпретировать графики траектории движения. 3. Провести эксперимент с пневматическим устройством: определить начальную скорость и проверить зависимость дальности полёта от угла броска с учётом сопротивления воздуха и без. Объект исследования - это тело, брошенное под углом к горизонту. Предмет исследования - дальность полёта Методы исследования: сбор информации, анализ информации, обобщение информации, изучение теоретического материала, физический эксперимент компьютерное моделирование исследуемого процесса в среде Microsoft Office Excel 2.Основная часть 2.1Анализ теоретического материала А) Движение тела, брошенного под углом к горизонту, часто называют баллистическим движением. Баллистика (греч. ballo ― бросаю) ― важная и древняя наука, которая применяется в военном деле, в криминалистике, в спорте и других сферах деятельности человека. Истоки баллистики теряются в древности. Самым первым ее проявлением было, несомненно, метание камней доисторическим человеком. Такие предшественники современного оружия, как лук, катапульта и баллиста, могут служить типичным примером самых ранних видов применения баллистики. Возникновение баллистики как науки относится к 16 в. Первыми трудами по баллистики являются книги итальянца Н. Тартальи «Новая наука» (1537) и «Вопросы и открытия, относящиеся к артиллерийской стрельбе» (1546). В 17 в. фундаментальные принципы внешней баллистики были установлены Г. Галилеем, разработавшим параболическую теорию движения снарядов, итальянцем Э. Торричелли и французом М. Мерсенном, который предложил назвать науку о движении снарядов баллистикой (1644). И. Ньютон провёл первые исследования о движении снаряда с учётом сопротивления воздуха - «Математические начала натуральной философии» (1687). В 17-18 вв. исследованием движения снарядов занимались: голландец Х. Гюйгенс, француз П. Вариньон, швейцарец Д. Бернулли, англичанин Робинс, русский учёный Л. Эйлер и др. Экспериментальные и теоретические основы внутренней баллистики заложены в 18 в. в трудах Робинса, Ч. Хеттона, Бернулли и др. В 19 в. были установлены законы сопротивления воздуха (законы Н. В. Маиевского, Н. А. Забудского, Гаврский закон, закон А. Ф. Сиаччи). Б) Баллистическое движение в поле тяготения Земли. Траектория баллистического движенияТраекторией тела, движущегося в поле тяготения Земли, является баллистическая кривая. Если считать поле тяготения однородным (что справедливо при начальной скорости тела, значительно меньшей первой космической), рассматривать движение тела вблизи поверхности Земли (т.е. кривизной поверхности Земли пренебречь) и, главное, пренебречь сопротивлением воздуха, то в первом приближении баллистической кривой будет парабола, описываемая графиком квадратичной функции 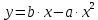 , где , где 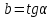 , , 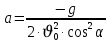 В рассматриваемом случае парабола проходит через начало координат и ветви параболы направлены вниз, так как коэффициент при В рассматриваемом случае парабола проходит через начало координат и ветви параболы направлены вниз, так как коэффициент при 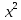 меньше нуля. меньше нуля.Основные параметры баллистического движения время подъема на максимальную высоту 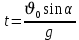 , , максимальная высота подъема 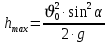 , , время полета 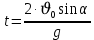 , ,дальность полета 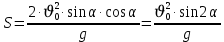 . . Скорость при баллистическом движенииСкорость тела, брошенного под углом к горизонту с начальной скоростью 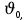 , в произвольной точке траектории можно рассчитать по формуле (5) прил. 3: , в произвольной точке траектории можно рассчитать по формуле (5) прил. 3: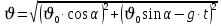 Направление вектора скорости в произвольной точке траектории определяется углом 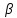 , образованным вектором скорости , образованным вектором скорости 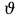 с осью х : с осью х :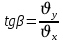 В)Движение в поле тяготения с учётом силы сопротивления воздуха. При движении снаряда в воздухе кроме силы тяжести на него действует сила сопротивления воздуха. Величина силы сопротивления воздуха, а следовательно, и интенсивность воздействия на снаряд, может значительно превосходить силу тяжести. Эта разница тем больше, чем меньше вес снаряда и больше скорость его полёта. Разнообразие форм современных пуль и снарядов во многом определяется необходимостью уменьшить величину силы сопротивления. Сила сопротивления воздуха является одним из главных факторов, препятствующих достижению больших дальностей стрельб. Сопротивление воздуха полёту вызывается тремя основными причинами: вязкостью воздуха, отрывом пограничного слоя с образованием завихрения, образованием баллистической волны. Вязкость воздуха объясняется наличием внутреннего сцепления между частицами воздуха. При движении снаряда происходит следующее явление. Частицы воздуха, непосредственно примыкающие к снаряду, вследствие сцепления с его поверхностью, движутся со скоростью снаряда. Следующий слой частиц воздуха в результате внутреннего сцепления также приходит в движение, но уже с несколько меньшей скоростью. Движение этого слоя передаётся следующему, и так до тех пор, пока разность скоростей частиц не станет равной нулю. Образуется так называемый пограничный слой . Пограничный слой образуется как при движении снаряда со скоростью меньшей скорости звука, так и при движении со скоростью большей скорости звука. В пограничном слое возникают касательные напряжения, которые можно отнести к силам трения. На их преодоление расходуется часть энергии снаряда, что и приводит к уменьшению скорости его полёта. Понятно, что тщательная обработка поверхности снаряда уменьшает сопротивление воздуха на всех скоростях. Если слой воздуха, раздвинутый головной частью снаряда, снова сомкнётся сразу за снарядом, то сопротивление воздуха будет наименьшим. Кинетическая энергия снаряда будет расходоваться только на раздвигание слоя воздуха и преодоление сил трения, возникающих в пограничном слое. Однако такого положения можно достигнуть только при наличии особой сигарообразной формы снаряда и при крайне малых скоростях его полёта. Реальные же скорости полёта современных снарядов во много раз превосходят скорости формирования ламинарного потока. При движении снаряда с плоским дном пограничный слой, достигнув донного среза, отрывается от него. За дном образуется разреженное пространство, куда засасываются частицы воздуха из пограничного слоя. Пограничный слой, скатываясь, образуя турбулентные завихрения . В связи с этим давление за донной частью ниже атмосферного, и снаряду приходится преодолевать эти разности давлений. При движении снарядов со скоростью меньшей скорости звука образование завихрения является главной причиной сопротивления воздуха. На характер завихрения особенно влияет форма хвостовой части. Конусообразная или каплевидная сходящаяся форма хвостовой части наиболее выгодна для снарядов, имеющих скорость меньшую скорости звука. Форма головной части имеет гораздо меньшее значение. Параметры движения зависят от безразмерной величины, которая называется коэффициентом аэродинамического сопротивления - Cx. Этот коэффициент зависит от плотности воздуха площади поперечного сечения тела. Также параметры полета зависят от формы тела, скорости полета и плотности атмосферы. Величина силы сопротивления возрастает особенно резко при движении снарядов со скоростями, превышающими скорость звука. Г)Расчет баллистической кривой Пусть из некоторой точки с начальной скоростью 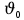 , направленной под углом , направленной под углом 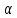 к горизонту, брошено тело. Примем за начало отсчёта точку, из которой тело брошено. Ось X направим горизонтально, а ось Y – вертикально (рис. 1). к горизонту, брошено тело. Примем за начало отсчёта точку, из которой тело брошено. Ось X направим горизонтально, а ось Y – вертикально (рис. 1).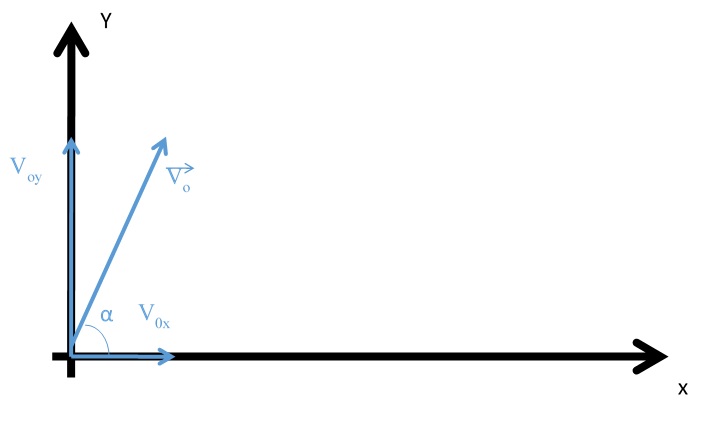 Рис. 1 Движение тела, брошенного под углом к горизонту, можно рассматривать как сумму двух независимых движений: равномерного движения по горизонтали (вдоль оси х силы не действуют, поэтому движение будет равномерным) и равнопеременного движения тела, брошенного вертикально вверх (сначала тело движется равнозамедленно, потом равноускоренно). Рассмотрим движение тела вдоль оси х. Проекция начальной скорости на ось х равна: 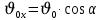 Так как на тело действует только сила тяжести, направленная по вертикали вниз, то тело движется с ускорением, которое называется ускорением свободного падения и направлено вертикально вниз. Проекция ускорения свободного падения на ось х равна нулю: 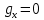 Следовательно, вдоль оси х тело движется равномерно, значит, проекция скорости на ось х в любой момент времени остаётся постоянной. 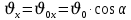 Расстояние от точки вылета тела до точки приземления называется дальностью полёта. Обозначим его S(рис.2). Р 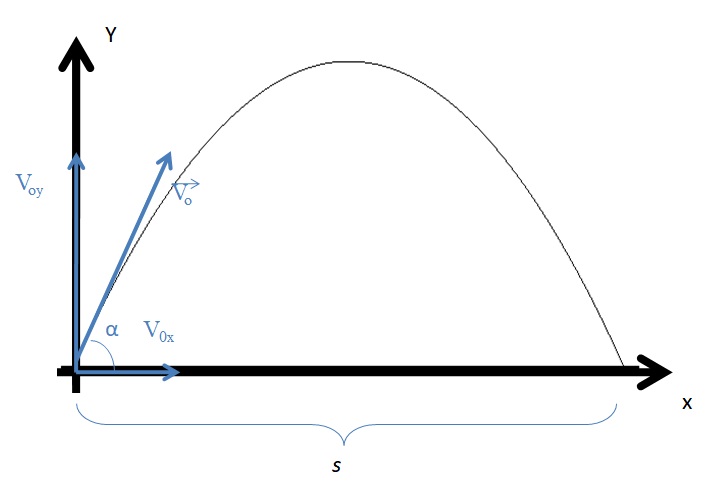 ис. 2 Для расчета дальности полёта воспользуемся формулой перемещения при равномерном движении: 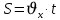 где t – время полёта. Координата х в любой момент времени t может быть вычислена по формуле координаты равномерного движения: 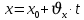 где 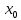 - начальная координата. - начальная координата.Рассмотрим теперь движение тела вдоль оси у. Проекция начальной скорости на ось у равна 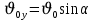 Проекция ускорения свободного падения на ось у неравна нулю 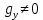 , ,поэтому движение тела вдоль оси у будет равноускоренным. Следовательно, проекция скорости на ось у в любой момент времени может быть вычислена по формуле 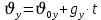 Высота подъёма тела вычисляется по формуле координаты для равноускоренного движения: 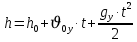 где 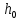 – начальная высота. – начальная высота.Координата у в любой момент времени вычисляется аналогично: 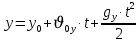 где 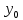 - начальная координата тела. - начальная координата тела.Чтобы определить траекторию, по которой движется тело, необходимо получить уравнение этой траектории. Для этого воспользуемся уравнениями координаты х равномерного движения и координаты у для равноускоренного движения: 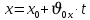 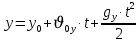 Рассмотрим движение тела из начала отсчёта, т.е 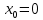 и и 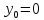 . Следовательно, . Следовательно, 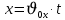 (1) (1)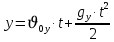 (2) (2)Из (1) следует 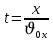 . Полученное значение времени t подставим в уравнение координаты y. . Полученное значение времени t подставим в уравнение координаты y.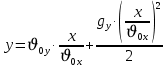 В выбранной системе координат 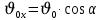 , , 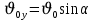 , а , а 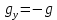 (ускорение свободного падения направлено вниз (в сторону, противоположную, направлению оси y), поэтому уравнение траектории движения тела, или зависимость у(х): (ускорение свободного падения направлено вниз (в сторону, противоположную, направлению оси y), поэтому уравнение траектории движения тела, или зависимость у(х):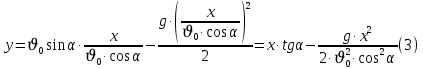 Между координатами получилась квадратичная зависимость. Значит траектория - парабола. В качестве постоянных членов уравнения параболы выступают: угол наклона 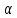 – в виде функции – в виде функции 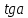 и и 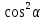 , , начальная скорость 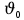 , ,ускорение свободного падения  . .2.2 Практическая часть Программа Microsoft Office Excel предоставляет графические инструменты для возможности создания табличных расчётов, с помощью которых совершается анализ данных и их дальнейшая графическая визуализация. Применяем программу Excel Описание действий 1)Постановка задачи Движение тела, брошенного под углом к горизонту Исследовать движение тела, брошенного под углом к горизонту при заданных начальной скорости v0 и угле бросания a, и следующих допущениях: тело мало и его можно считать материальной точкой; тело движется вблизи поверхности Земли, т. е. ускорение свободного падения постоянно и равно 9,8 м/с^2; начало системы координат расположено в точке бросания; сопротивлением воздуха можно пренебречь. Пусть v0 начальная скорость (м/с), t- время движения (с), X- дальность полёта Построение компьютерной модели движения, брошенного под углом к горизонту в MS Excel Модель1 Моделирование движения тела, брошенного под углом к горизонту (без учета сопротивления воздуха) Построить траекторию движения при v0= 21,6 м/с a= 15 град Электронная таблица, моделирующая баллистическое движение, в формате отображения формул представлена на рисунке. По рассчитанным значениям координат x, y строится баллистическая кривая 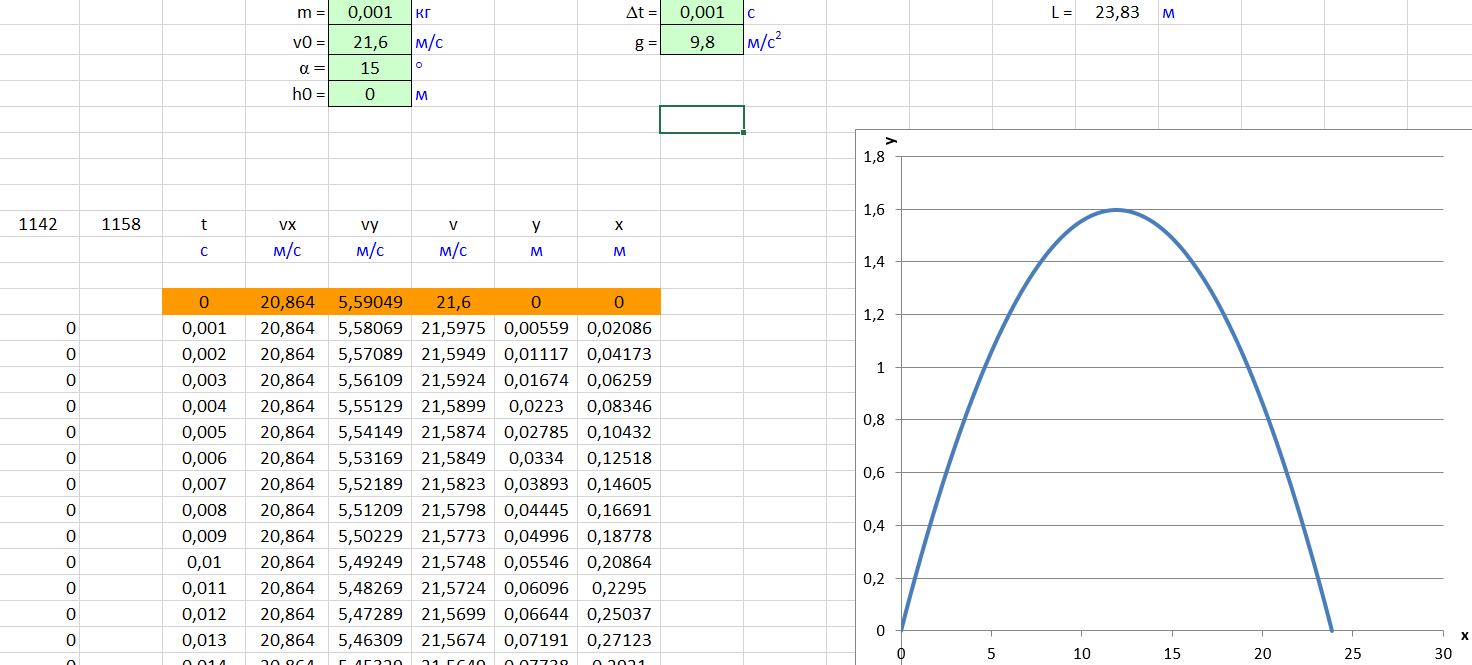 Рис. ВЫВОД: При использовании программы Excel была создана траектория движения тела, брошенного под углом к горизонту. Начальная скорость равна 21.6 м/с и угол равный 15 град. Траектория движения парабола. Пошаговое построение компьютерной модели тела в среде MS Excel: 1. Обусловим начальные характеристики, которые включают в себя 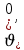 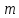 , , 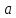 , , 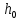 , g, Δt, и вставим их значения в ячейки F5 F6 F7 F8 J5 J6 соответственно. , g, Δt, и вставим их значения в ячейки F5 F6 F7 F8 J5 J6 соответственно. 2. Вводим начальные условия движения тела в ячейки D16, E16, F16 , G16 , H 16 , I 16, в соответствии с выбранной системой координат, среди которых t, 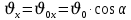 , , 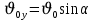 , ,  , ,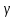 , , 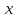 . После проставления начальных условий называем столбцы, включающие их. . После проставления начальных условий называем столбцы, включающие их. В электронных таблицах аргументы функций 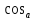 и и 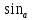 задаются в радианах, поэтому необходимо преобразовать значения углов из градусов в радианы с помощью умножения заданных углов на задаются в радианах, поэтому необходимо преобразовать значения углов из градусов в радианы с помощью умножения заданных углов на 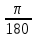 . .Чтобы получить 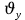 для каждого промежутка времени равного Δt = 0,001 c нужно учесть, что на рассматриваемое нами тело, движущееся сначала равнозамедленно, потом равноускоренно действует g, таким образом тело движется с ay= -g. Следовательно, для каждого промежутка времени равного Δt = 0,001 c нужно учесть, что на рассматриваемое нами тело, движущееся сначала равнозамедленно, потом равноускоренно действует g, таким образом тело движется с ay= -g. Следовательно, 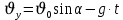 Выяснить, как зависит дальность полета от угла бросания при постоянной начальной скорости. Модель 2. Зависимость дальности полёта от угла бросания при постоянной скорости. Без учёта сопротивления воздуха: 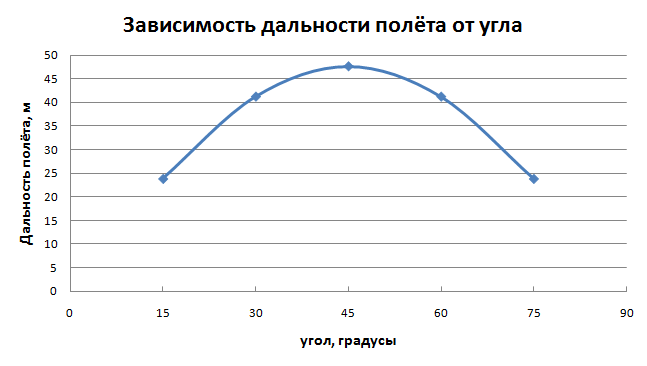 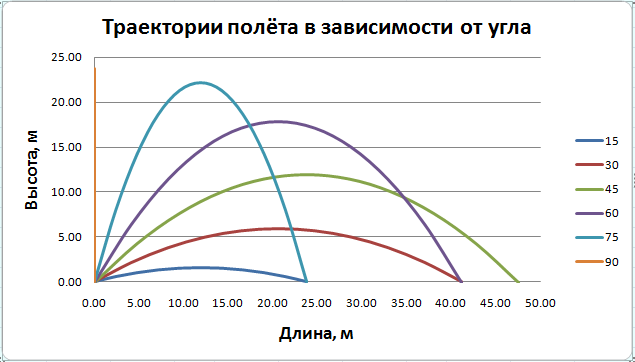
С учётом сопротивления воздуха: 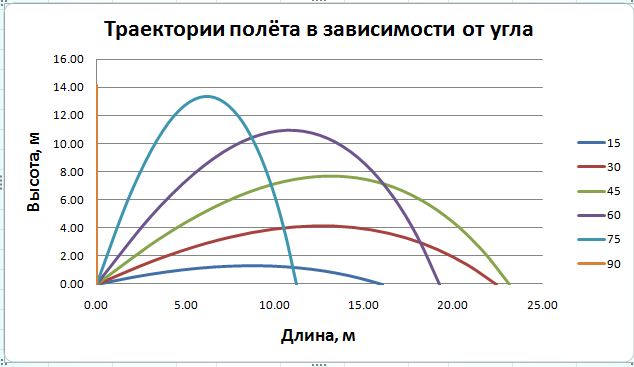 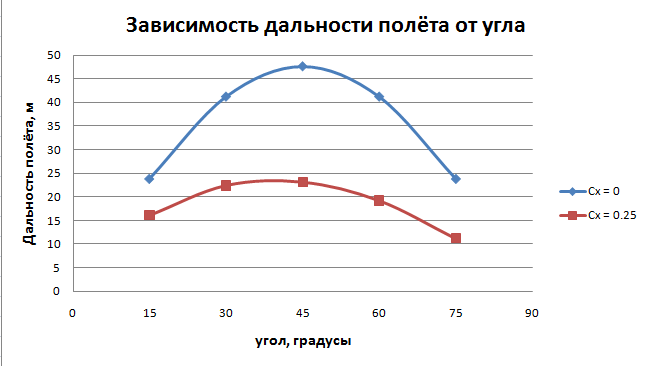
Вывод: Основываясь на выбранных данных, наибольшая дальность полёта составляет для угла 45 град с учётом и без учёта сопротивления воздуха. При углах меньше 45 град дальность полёта с учётом сопротивления воздуха меньше. Тоже наблюдается для углов больше 45 градусов. Таким образом сила сопротивления воздуха значительно влияет на дальность полёта( уменьшает) . Наличие коэфицента аэродинамического сопротивления значительно влияет Выяснить, как зависит дальность полёта от начальной скорости при постоянном угле бросания (построить график зависимости дальности полета от начальной скорости бросания ) Модель 3. Зависимость дальности полёта от начальной скорости, если угол броска не меняется. Без учёта сопротивления воздуха: 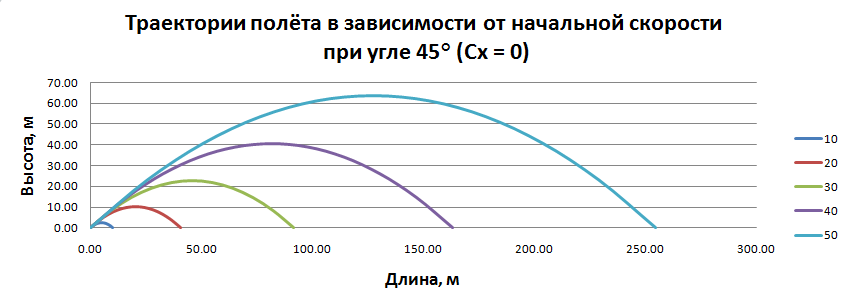 Зависимость дальности полёта от начальной скорости. 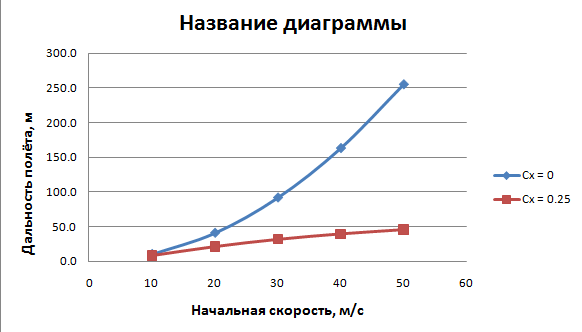 С учётом сопротивления воздуха: 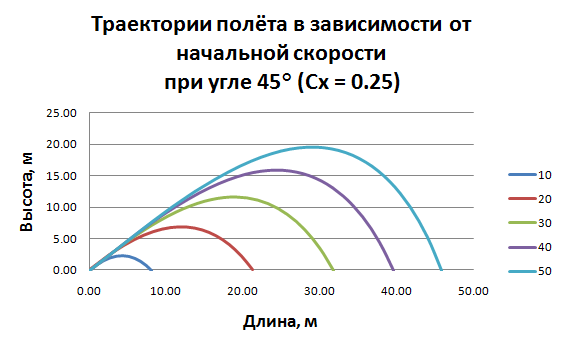 Вывод: В результате исследования дальности полёта от начальной скорости можно сделать вывод о том, что зависимость дальности полёта без учёта сопротивления воздуха представляет собой параболическую кривую, а зависимость дальности полёта с учётом сопротивления воздуха представляет собой кривую, которая стремится к некоторому предельному значению дальности полёта. С увеличением начальной скорости дальность полёта увеличивается в обоих случаях. Физический эксперимент: 2.Лабораторная работа по теме: Исследование зависимости дальности полёта от угла броска Цель: определить начальную скорость игрушечного пневматического пистолета. Выявить зависимость дальности от угла броска Оборудование: пневматический пистолет с поролоновыми пулями, транспортир, скотч, рулетка, секундомер Ход работы: 1.Определение начальной скорости пули. Для определения нач. скорости. Стреляем горизонтально замеряем время полёта и дальность полёта. Так как по оси x скорость не меняется, а угол при выстреле равен 0, то скорость определяется по формуле скорости равномерного движения. V= L/t В ходе работы были получены след. результаты
2.Определение скорости пули с помощью программы Audacity. Программа Audacity фиксирует звук выстрела и звук попадания Объяснение метода и результаты. Выбираем определённые расстояния (2 м, 4 м, 6.7 м). С помощью программы Audacity определяем промежутки времени начала и конца выстрела опыты проводим по 5 раз для каждого расстояния. Определяем среднюю скорость для данного расстояния. Получаем 3 значения средней скорости выстрела. Строим график зависимости скорости от времени. Получаем три точки. С помощью программы Excel достраиваем кривую до момента времени равного нулю. Это и будет начальная скорость пневматического пистолета. Расчёты производили для детского пистолета Nerf
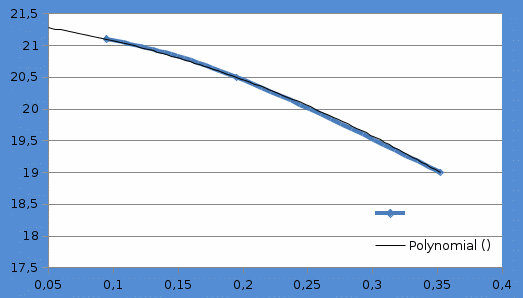 Вывод: Графическим способом определена начальная скорость пули в пневматическом пистолете, она равна 21.5 м/с 2.Исследование зависимости дальности полёта от угла броска Опыт производится в воздухе ,в школьном коридоре. Прикрепляем пневматический пистолет к транспортиру, задаём определённый угол и производим выстрел. Замеряем рулеткой дальность полёта.
Вывод: наибольшая дальность полёта достигается при угле 45 град. Зависимость дальности полёта от угла броска без сопротивления воздуха Расчёт по формуле дальность полета 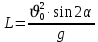 Vo=21,5 м/с Vo=21,5 м/с
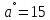 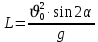 L= 21,5*21,5*0,5/10= 23,3м L= 21,5*21,5*0,5/10= 23,3м 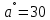 L= 21,5*21,6* 0,85/10 = 39,6 м L= 21,5*21,6* 0,85/10 = 39,6 м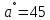 L= 21,6*21,5/10 = 46,6 м L= 21,6*21,5/10 = 46,6 м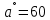 L= 21,5*21,5* 0,87/10 = 40,6 м L= 21,5*21,5* 0,87/10 = 40,6 мВывод: дальность полёта без учёта сопротивления воздуха значительно больше. Сопротивление воздуха оказывает значительное воздействие на движение тела. Наибольшая дальность полёта так же для угла 45 градусов. 3.Вывод В ходе исследований получены следующие результаты: Тело, брошенное под углом к горизонту двигается по кривой – параболе Дальность полёта зависит от угла броска и начальной скорости. Наибольшая дальность полёта наблюдается для угла 45 град Сила сопротивления воздуха влияет на дальность полёта, тем самым уменьшая её. Это проверено с помощью моделирования в среде Excel и в процессе физического эксперимента. В ходе анализа теоретического материала установлены причины, обуславливающие силу сопротивления воздуха: вязкость воздуха – объясняется наличием сцепления между молекулами воздуха. Пограничный слой – частицы воздуха к поверхности тела, проявляются силы трения. 3.Завихрения воздуха . Пограничный слой, скатываясь, образуя турбулентные завихрения, которые зависят от формы тела 6. Параметры движения зависят от величины, которая называется коэффициентом аэродинамического сопротивления - Cx. Этот коэффициент зависит от плотности воздуха площади поперечного сечения тела. Также параметры полета зависят от формы тела, скорости полета и плотности атмосферы. Список используемых источниковМякишев, Г.Я. Физика 10 кл. – М.: Просвещение, 2010. В. Дроздов. Парабола как баллистическая кривая, Журнал «Физика». 2008, № 12 Лавренов С.М. Exel. Сборник примеров и задач. – М.: Финансы и статистика, 2006. Баллистика (наука) http://knowledge.su/b/ballistika-nauka Энциклопедия Кругосвет http://www.krugosvet.ru/enc/nauka_i_tehnika/voennaya_tehnika/BALLISTIKA.html?page=0,0 Википедия. Баллистика https://ru.wikipedia.org/wiki/%D0%91%D0%B0%D0%BB%D0%BB%D0%B8%D1%81%D1%82%D0%B8%D0%BA%D0%B0 |