Репетитор по физике и математике Волович Виктор Валентинович Математика

• Название: Репетитор по физике и математике Волович Виктор Валентинович Математика
• Дата: 10.08.2018
• Размер: 449.79 Kb.
• Имя файла: FormMat.docx
• Тип: Документы; #49075

Репетитор по физике и математике – Волович Виктор Валентинович Математика

www.educon.by Все главные формулы по математике

Все главные формулы по математике

Оглавление

Формулысокращенногоумноженияиразложениянамножители 2

Квадратноеуравнение 2

Парабола 3

Степениикорни 3

Логарифмы 4

Прогрессии 4

Тригонометрия 5

Тригонометрическиеуравнения 8

Планиметрия 8

Стереометрия 13

Координаты 14

Таблицаумножения 14

Таблицаквадратовдвухзначныхчисел 15

• Формулы сокращенного умножения и разложения на множители

• Формулы сокращенного умножения:

(a b)²  a²  2ab b² (a b)²  a²  2ab b² a²  b²  (a b)(a b)

a³  b³  (a b)(a²  ab b² ) a³  b³  (a b)(a²  ab b² ) (a b)³  a³  3a²b 3ab²  b³ (a b)³  a³  3a²b 3ab²  b³

Последние две формулы иногда удобнее использовать в следующем виде:

(a  b)³  a³  b³  3ab(a  b) (a  b)³  a³  b³  3ab(a  b)

азложе

Р ние квадратного трехчлена на множители:

1 2

ax²  bx  c  a(x  x )(x  x )

е

^{е: x}1 <sup>и

гд x</sup>2 ^{– корни уравнения: ax² + bx + c = 0, у которого D > 0 (т.е. имеется два корня). Или:}

0

ax²  bx  c  a(x  x )<sup>2

гд : x</sup>0 ^{– единственный корень уравнения: ax² + bx + c = 0, у которого D = 0. Если корней у трехчлена нет,}

то на множители он не раскладывается.

• Квадратное уравнение

Если D > 0, то имеется два корня:

ax²  bx  c  0

D  b²  4ac

(a ≠ 0)

b D

x 

1,2 _2a

Если D = 0, то имеется один корень (его кратность: 2):

_{x } b

Если D < 0, то корней нет.

⁰ 2a

Теорема Виета (выполняется только если оба корня существуют, т.е. в случае когда D > 0):

x  x   ^b x  x  ^c

1 2 _a 1 2 _a

• Парабола

График параболы задается квадратичной функцией:

f(x) = ax² + bx+ c (a ≠ 0)

Если a > 0, то ветви параболы направлены вверх, если a < 0, то ветви параболы направлены вниз, при этом координаты вершины параболы:

x  <sup>b

в</sup>2a

_{2 b}2

y_в y_{maxa0}  y_{mina0}  ax_в bx_в c  c  _4a Парабола всегда пересекает ось OY в точке: (0; с).

• Степени и корни

• Свойства степеней:

_a pg _{ a} p _{ a}g



p

1. 
    a _ag
   

p g

_ap_^g _{ a}g_^p _{ a}pg
^ap  ^a ^p p ^{  }b

1. 
    
   

(a b) ^p  a ^p b^p

a ⁰ = 1 a ¹ = a 1 ⁿ = 1

0 ⁿ= 0; при n > 0, ноль можно возводить только в положительную степень.

_an 1 1

 aⁿ

1. Свойства корней:

_an _an

Если m – целое, n – натуральное, то для любого a> 0 справедливо:

m _m
aⁿ  ⁿ a^m  _ⁿ a_

Для любых натуральных m и n, а также любых a  0 и ^{b  0} справедливы равенства:

ⁿ a b

 ⁿ a  ⁿ b
n

b

a

n _a

n _b

 (при b  0 )
^m n _a

ⁿ m <sub>a

 </sub> nm_a

n <sub>a

</sub> nm _am

Для арифметических корней:
_ⁿ a_ⁿ  a

Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a  0 . Для корня нечетной степени выполняется также следующее равенство:

2n1 _{x  }2n1 _x

Для корня четной степени:

2n _x2n _{
x } <sup>x,

</sup>x,


x  0,

x  0.

• Логарифмы

^{Определение логарифма: если log}a ^{x = b, то a b}= x, при: a > 0, x > 0, a ≠ 1. Или:

_alog_ax _{ x}

1. Свойства логарифмов:

^loga <sup>a=1

log</sup>a ^{1 = 0}


log_a b 

1

log_b a

^loga ^{(xy) = log}a ^{x + log}a ^y

log

^{ x }  log

a  _y 

 
_a x  log_a y

^loga ^xk= kloga|x|; при х≠ 0, если k – четное число. loga x^k= klogax; при x > 0, если k – любое другое число.

a

log _k

x  ¹ log

_k a

x; при а≠ 0 и а≠ ±1, если k – четное число.




a

log _k

x  ¹ log

_k a
x; при a > 0 и а≠ 1, если k – любое другое число.




log

x  ^{logc x}; при c > 0, c ≠ 1.

c

^a log a
_alog_bc _{ c}log_ba

• Прогрессии

• Арифметическая прогрессия:

^a_n ^{ a}₁ ^{ d} ^{n 1}

a_n  a_n1  d






^2an ^{ a}n1 ^{ a}n1

_{S } a₁  a_{n  n } 2a₁  d (n 1) _{ n}

ⁿ 2 2

1. Геометрическая прогрессия:

a_m  a_n  a_k  a_p; при: m + n = k + p.

1

n

b  b  q^n1

b_n  b_n1  q

b  b

2

n n1

^bn1

b (1 qⁿ )

_{Sn }1

1 q

S  ^b1 ; при: q  1 .
беск.убыв. _{1 q}

b_m b_n  b_k b_p; при: m + n = k + p.

• Тригонометрия

• Основное тригонометрическое тождество:

sin² x  cos² x  1

Основные тригонометрические формулы. Пусть имеется прямоугольный треугольник, изображенный на рисунке, тогда:

sin x  ^a

c

cos x  ^b

c

_{tg x } a _ sin x

b

ctg x  ^b 

cos x

1 _ cos x

1. Формулы двойного угла:

tg² x1 
ctg² x1 
1

cos² x

1

sin² x

a tg x

sin x



sin 2x = 2sin x cos x

₌ 2tg x

1 tg² x

1 tg² x


cos 2x = cos² x  sin² x = 2cos² x 1 = 1 2sin² x

⁼ 1 tg² x


2tg x

1 tg² x _ ctg² x 1



^{tg 2x =} 1 tg² x

ctg 2x =

2tg x 2 ctg x

1. Формулы сложения:

sin(x  y)
= sin x cos y  cos x sin y

sin(x  y) = sin x cos y  cos x sin y

cos(x  y) cos(x  y)

= cos xcos ysin xsin y

= cos xcos y sin xsin y

tg(x  y) = ^{tg x  tg y}

1 tg x  tg y

tg(x  y)

₌ tg x  tg y

1 tg x  tg y


ctg(x  y)

₌ 1 tg x  tg y _ ctg x ctg y 1

tg x  tg y ctg y  ctg x

ctg(x  y)

₌ 1 tg x  tg y _ ctg x ctg y 1


tg x  tg y

1. Формулы преобразования суммы в произведение:

ctg y  ctg x



sin x  sin y

_{= 2sin}  ^{x  y}  _cos  ^{x  y} 


 ₂   ₂ 

sin x  sin y

   

_{= 2 cos}  ^{x y} _sin  ^{x y}


 ₂   ₂ 

   

cos x cos y= 2 cos ^{ x y} cos ^{ x y}

 ₂   ₂ 

   

cos x cos y= 2sin ^{ x y} sin ^{ x y}

 ₂   ₂ 

   

_{tg x  tg y =} sin(x  y)

cos x  cos y

_{tg x  tg y =} sin(x  y)

cos x  cos y

^sin  ^{y  x}

ctg x  ctg y =

sin x sin y

^sin  ^{y x}


ctg x  ctg y =

sin x sin y

1. Формулы преобразования произведения в сумму:

sin x sin y =

¹ _cos _x  y _ cos _x  y _

2

1. Формулы понижения степени:

sin x cos y=
cos x cos y=

¹ _sin _x  y_ sin _x  y _

2

¹ _cos _x  y_ cos _x  y _

2

_sin2 x ₌ 1 cos x

2 2

_cos2 x ₌ 1 cos x

2 2

_tg2 x ₌ 1 cos x

2 1 cos x

_ctg2 x ₌ 1 cos x

1. Формулы половинного угла:

2 1 cos x
_{tg x} sin 2x _ 1 cos 2x

1. Формулы приведения:

1. Тригонометрическая окружность:

1 cos 2x

_{ctg x} 1 cos 2x _

sin 2x

sin 2x sin 2x

1 cos 2x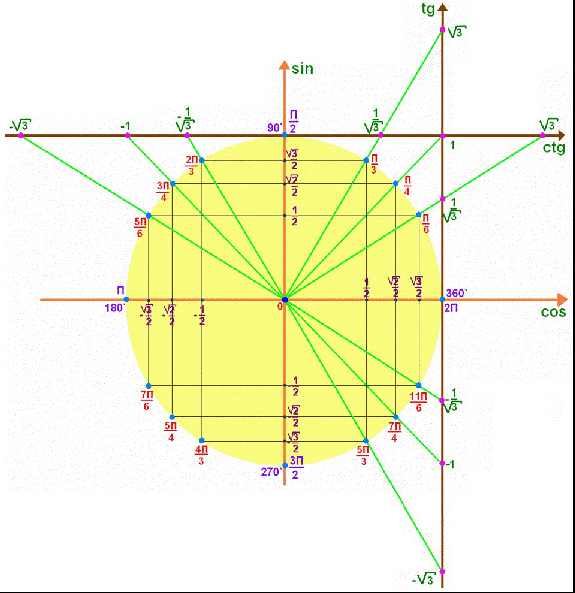

• Тригонометрические уравнения

Формулы решений простейших тригонометрических уравнений. Решение уравнения вида sin x = a, может быть записано двумя равнозначными способами:


sin x a 

^x ^1^{n arcsin a  n,}

n  Z



^{arcsin a 2k, k  Z}

sin x a 

^{x } arcsin a 2k,

k  Z

Решение остальных уравнений записывается единственным образом:

cos x a 

x  arccos a 2n,

n  Z



Некоторые частные случаи:

tg x a 

ctg x a 

x arctg a n,

x arcctg a n,

n  Z

n  Z


sin x 0 

x n,

n  Z



sin x  1 
sin x  1 
cos x 0 

  2n, 2
_x 

_x 

_x 

   2n, 2
  n, 2

n  Z
n  Z
n  Z


cos x  1 

x 2n,

n  Z


cos x  1 

x  2n,

n  Z


_x 

tg x 0 

x n,

n  Z



ctg x 0 

  n, 2

n  Z

• Планиметрия

Произвольный треугольник (a, b, c – стороны треугольника, r – радиус ^{вписанной окружности, R – радиус описанной окружности, h}a ^{– высота опущенная на сторону a, h}b ^{– высота опущенная на сторону b, h}c ^{– высота опущенная на сторону c, l}a ^{– биссектриса опущенная на сторону a, m}a ^{– медиана} опущенная на сторону a).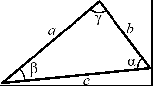

Сумма углов треугольника:

      180  рад

Площадь_произвольной_фигуры_в_которую_можно_вписать_окружность'>Площадь_прямоугольника'>Площадь'>Площадь треугольника через две стороны и угол между ними:

S = ¹ absin γ

2

Площадь треугольника через основание и высоту опущенную на это основание:

^{S = 1 bh}b

2

Площадь треугольника (формула Герона):

p( p a)( p b)( p c)

S 


где:

_p a b c

2

– полупериметр. Площадь треугольника через радиус описанной окружности:

_{S } abc

4R

Формула медианы: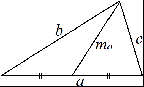

1

2

2(b²  c² )  a²

Свойство биссектрисы:

m_a 

с

о

Ф рмулы биссектрисы:

b _ b₁ c c₁


bc b₁c₁

l_a 

l_a 

cb(b c a)(b c a) c  b


О новное свойство высот треугольника:

h_{a } h_b

b a

Формулы высоты:

h_a 
2

a

p( p a)( p b)( p c)

1 _ 1 _ 1 _ 1



Теорема косинусов:

h_a h_b h_c r

a² = b² + c² –2bccos α

Теорема синусов:

a

sin

_ b

sin 

_ c

sin 

 2R

Правильный треугольник (все стороны равны а). Радиус окружности, вписанной в правильный треугольник:

a 3

6

r 

a 3

3

Радиус окружности, описанной около правильного треугольника:

R 

_a2

3

Площадь правильного треугольника:

S 

4

Прямоугольный_треугольник'>Прямоугольный треугольник (a, b – катеты, с– гипотенуза). Теорема Пифагора:

с² = a² + b² Радиус окружности, вписанной в прямоугольный треугольник:

_{r } a  b  c

2

Радиус окружности, описанной около прямоугольного треугольника:

R  ^c

2


Площадь прямоугольного треугольника:

S  ¹ ab  ¹ hc

2 2

Свойства высоты, опущенной на гипотенузу прямоугольного треугольника: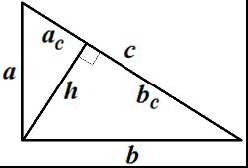



рапец

h²  a b

c c

c

a²  a  c

c

b²  b  c

Т ия (a, b – основания, h – высота). Средняя линия трапеции:

_{l } a  b

2

Площадь трапеции: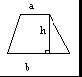



S  l  h  ^{a  b}  h

2

Параллелограмм. Площадь параллелограмма через сторону и высоту опущенную на неё:

S = bh

Площадь параллелограмма через две смежные стороны и угол между ними:

S = absin γ

Квадрат. Площадь квадрата через сторону: Площадь квадрата через диагональ:
S = a²
S  ¹ d ²

2

^{Площадь ромба через две диагонали d}1 ^{и d}2^{, а также через угол между равными сторонами а:}

S  ¹ d d
 a² sin 

₂ 1 2

Площадь прямоугольника через две смежные стороны:

S = ab

1. Площадь произвольного выпуклого четырехугольника через диагонали и угол между ними:

S  ¹ d d
sin

₂ 1 2

Площадь произвольной фигуры в которую можно вписать окружность (в т.ч. площадь любого треугольника) может быть рассчитана через радиус вписанной окружности и полупериметр по очень важной формуле:

S = pr
По этой же формуле часто удобно находить и радиус вписанной окружности в некоторый многоугольник,

в который её удалось вписать (в т.ч. любой треугольник):

r  ^S

p

1. Свойства хорд и касательных:

1. Теорема о пропорциональных отрезках хорд:

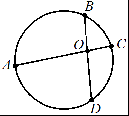BOOD = AOOC

1. Теорема о касательной и секущей и о двух секущих:

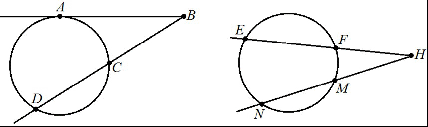BA² = BCBD HFHE =HMHN

1. Свойства центральных и вписанных углов:

1. Свойство центральных углов и хорд:

_{ } 

2

1. Свойство центральных углов и секущих:

_{ } 

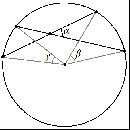2

Окружность вписана в четырёхугольник (условие, когда это возможно):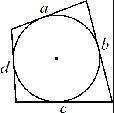

a + c = b + d

Окружность описана около четырехугольника (условие, когда это возможно):




у

С мма углов n-угольника:

α + γ = β + φ = 180
₁ ₂  ... _n 180 (n 2)   (n 2) рад


ентрал

Ц ьный угол правильного n-угольника:

_{ } 360 _ 2

n n



рад

^{Площадь правильного многоугольника (a}n ^{– сторона правильного n-угольника, r – радиус вписанной} окружности):

_{S } n  a_n  r

2

Длина окружности (здесь и далее R – радиус окружности или круга):

L = 2πR

1. Длина дуги окружности:

1. Площадь круга:

1. Площадь кругового сектора:

^Lдуги ⁼

  R_град

180
S = πR²
^{= α}рад <sup>R


S</sup>сектора

₌  R² _град

360

₌ _рад R²

2

Площадь кольца (R – радиус внешней окружности, r – радиус внутренней окружности):

S  _R²  r² _

Площадь кругового сегмента ( 0   ; –угол в радианах):

_R2

^S ^{ sin} 2

• Стереометрия

Куб (а– сторона куба, d – главная диагональ). Главная диагональ куба:

3

d  a

Объем куба:

V  a³

Прямоугольный параллелепипед (a, b, c – его измерения, d – главная диагональ). Объем:

V  abc

Главная диагональ прямоугольного параллелепипеда:

d ²  a²  b²  c²

Призма (h – высота призмы). Объем призмы:

^{V = S}осн^h

Прямая призма (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):

^Sбок ^{= Pl = Ph}

Цилиндр (R – радиус основания, h – высота цилиндра). Объем цилиндра:

б
л

V = πR²h


П ощадь боковой поверхности цилиндра:

О ъем пирамиды (h – высота пирамиды):

^Sбок ^{= 2πRh}

_{V =} S_осн  h

3

Правильная пирамида (P – периметр основания, l – апофема, т.е. высота боковой грани). Площадь боковой поверхности:

^Sбок

 ¹ Pl

2

Объем конуса (R – радиус основания, h – высота конуса):

 R² h

V =

3

1. Площадь боковой поверхности конуса:

где: l – длина образующей: l 

Объем шара (R – радиус шара):

^Sбок ^=πRl
h²  R²

.

V = ⁴ πR³

3

Площадь поверхности сферы (R – радиус сферы):

S = 4πR²

• Координаты

^{Числовая ось. Пусть координата начала отрезка АВравна х}1, ^{а координата конца х}2. ^{Тогда длина отрезка} находится по формуле:

AB  x₂  x₁

Координату середины отрезка находят по формуле:

_{x } x₁  x₂

c ₂
^{Координатная плоскость. Пусть координаты начала отрезка АВравны: А(х}1^{; у}1^{), а координаты конца: В(х}2^{; у}2^{). Тогда длина отрезка находится с помощью теоремы Пифагора по формуле:}



x x  y  y



2



2 1



2

2 1

AB 

Координаты середины отрезка находят по формулам:


_{x } x₁  x₂

c ₂

у_c 

у₁  у₂

2

^{Трехмерная система координат. Пусть координаты начала отрезка АВравны: А(х}1^{; у}1^{; z}1^{), а координаты конца: В(х}2^{; у}2^{; z}2^{). Длина отрезка находится по формуле:}



x  x  y y  z



2





2





2

2 1

2 1

2 1

• 
  z
  
• 
  AB 
  

Координаты середины отрезка находят по формулам:

_{x } x₁  x₂

c ₂

у_c 

у₁  у₂

2

_{z } z₁  z₂

^c 2

• Таблица умножения

Одно из умножаемых123456789Второе из умножаемых11234567892468101214161839121518212427416202428323652530354045636424854749566386472981

• Таблица квадратов двухзначных чисел

Десятки0123456789Единицы0010040090016002500360049006400810011121441961168126013721504165618281241444841024176427043844518467248464391695291089184928093969532968898649416196576115619362916409654767056883652522562512252025302542255625722590256362566761296211631364356577673969216749289729136922093249448959297569940986432478414442304336446246084774496049813618411521240134814761624179219801