Практическая работа по математике ММУ. Практическа работа. Решение Домножаем числитель и знаменатель на выражение, сопряженное к знаменателю
 Скачать 0.7 Mb. Скачать 0.7 Mb.
|
|
Задания для практических занятий 1. Выполнить деление комплексных чисел:  Решение: Домножаем числитель и знаменатель на выражение, сопряженное к знаменателю: 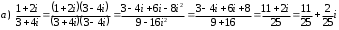 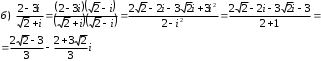 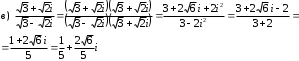 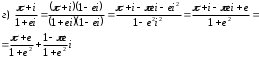 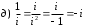 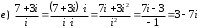 2. Вычислить пределы последовательностей 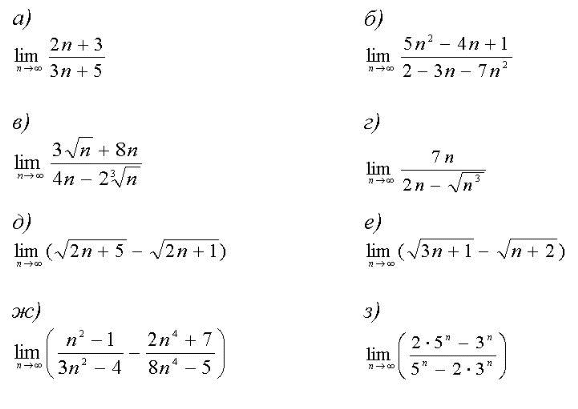 Решение: 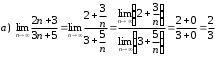 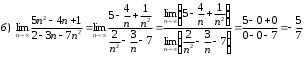 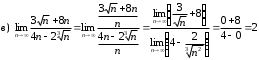 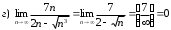 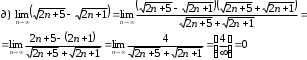 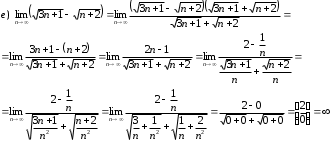 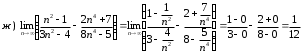 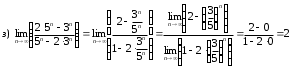 3. Используя признаки Даламбера и Коши исследовать сходимость рядов: 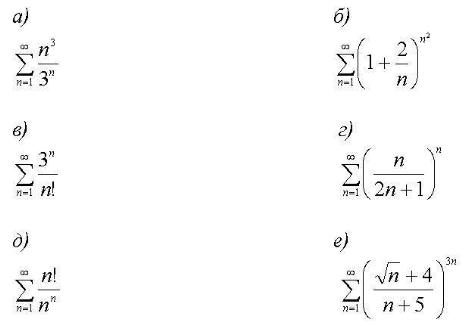 Решение: Признак Даламбера: D = 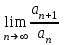 , если D < 1 , то ряд , если D < 1 , то ряд 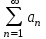 сходится, а если D > 1 , то расходится. сходится, а если D > 1 , то расходится.Признак Коши: 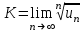 , если К < 1, то ряд , если К < 1, то ряд 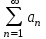 сходится, а если К > 1 , то расходится. сходится, а если К > 1 , то расходится.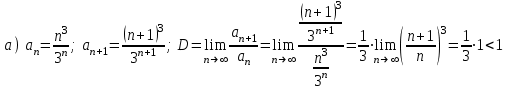 Значит ряд сходится по признаку Даламбера. 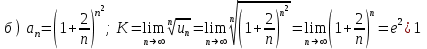 Значит ряд расходится по признаку Коши. 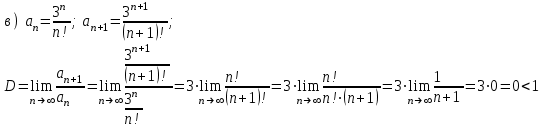 Значит ряд сходится по признаку Даламбера. 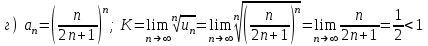 Значит ряд сходится по признаку Коши. 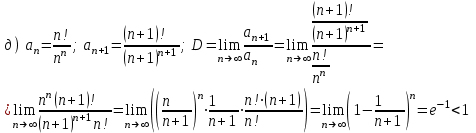 Значит ряд сходится по признаку Даламбера. 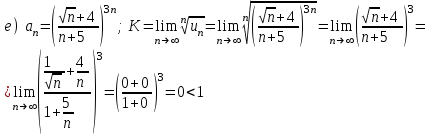 Значит ряд сходится по признаку Коши. 4. Найти производные сложных функций 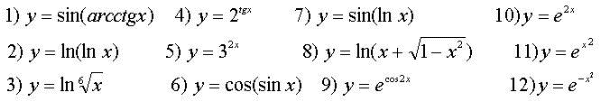 Решение: 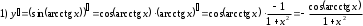 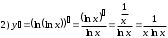 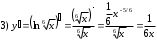 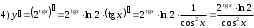 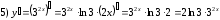 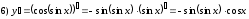 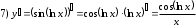 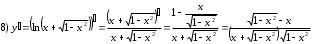 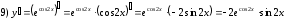 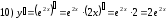 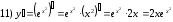 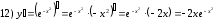 5. Вычислить неопределенный интеграл 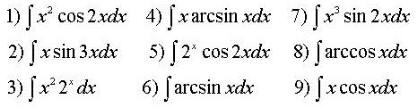 Решение: Метод интегрирования по частям 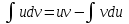 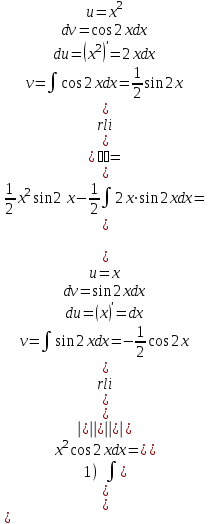 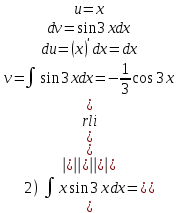 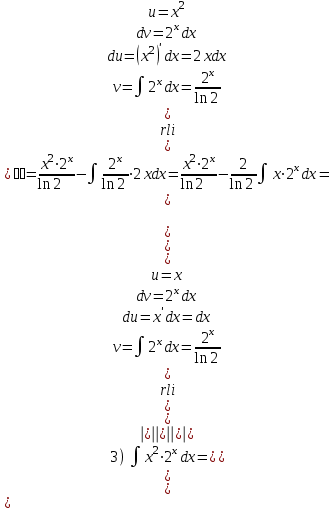 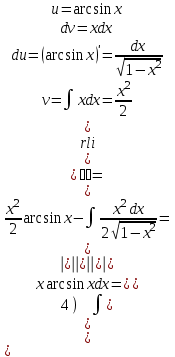 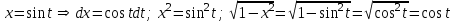 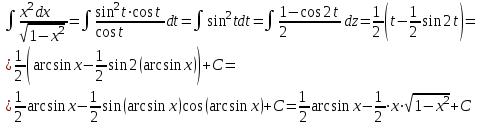 Тогда 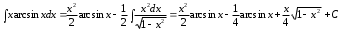 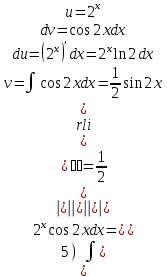 Снова применяем формулу интегрирования по частям: 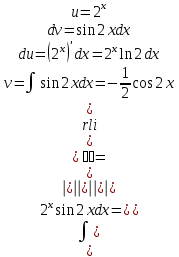 Тогда: 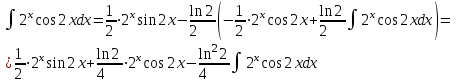 Получили реккурентную формулу: 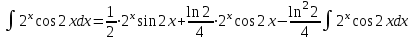 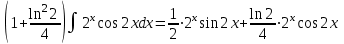 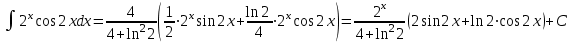 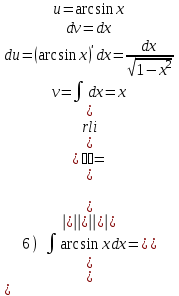 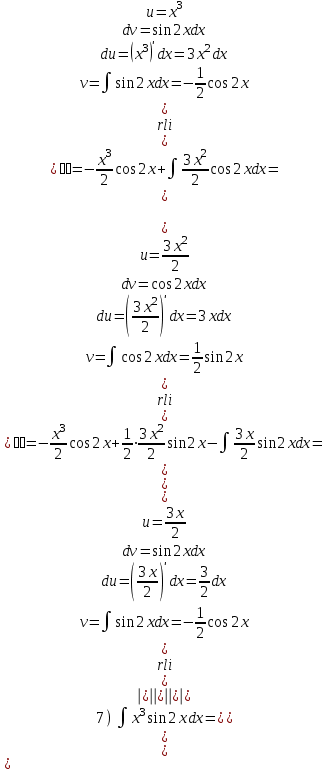 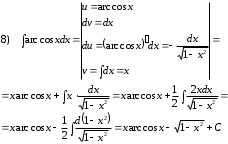 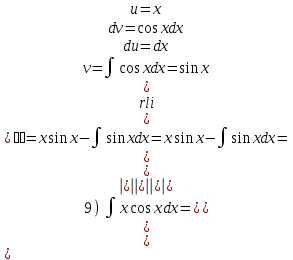 6. Найти частные производные первого и второго порядка: 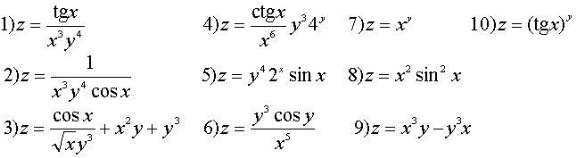 Решение: Находим частную производную 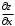 по аргументу х, считая, что у = const , потом находим частную производную 2-го порядка по аргументу х, считая, что у = const , потом находим частную производную 2-го порядка 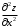 как частную производную по аргументу х от частной производной как частную производную по аргументу х от частной производной 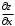 считая, что у = const . Аналогично находим считая, что у = const . Аналогично находим 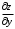 и и 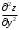 , считая, что х = const. Потом находим смешанную производную 2-го порядка , считая, что х = const. Потом находим смешанную производную 2-го порядка 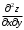 . .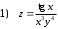 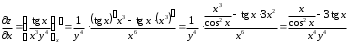 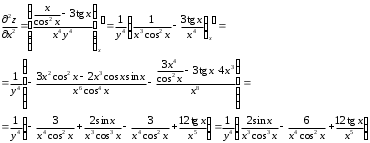 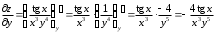 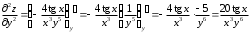 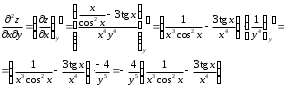 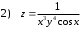 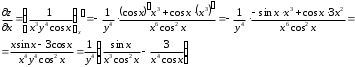 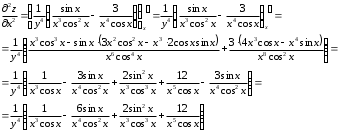 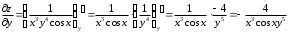 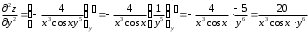 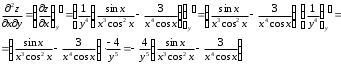 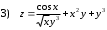 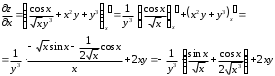 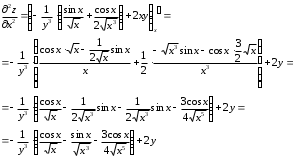 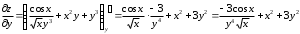 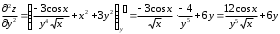 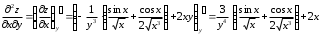 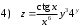 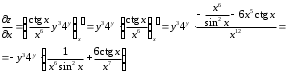 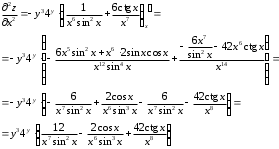 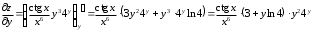 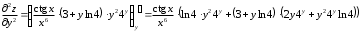 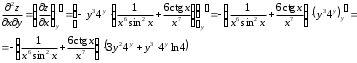 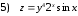 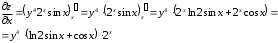 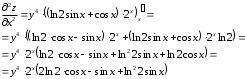 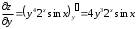 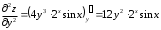 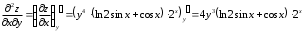 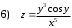 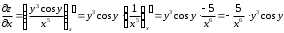 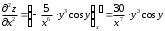 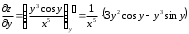 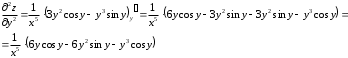 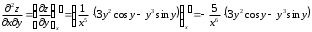 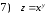 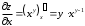 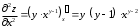 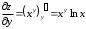 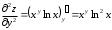 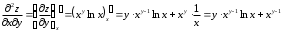 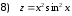 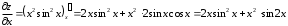 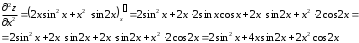 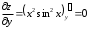 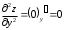 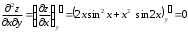 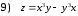 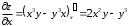 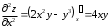 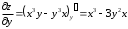 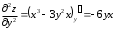 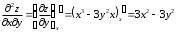 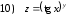 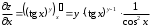 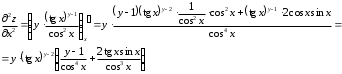 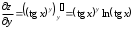 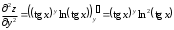 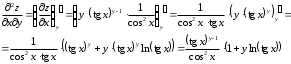 7. Найти: a. Произведение b. Сумму матриц 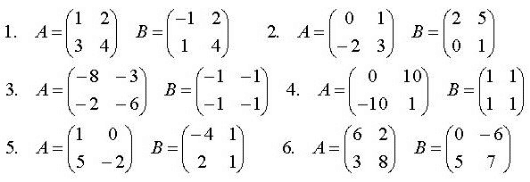 Решение: Произведение матриц: 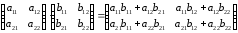 Сумма матриц: 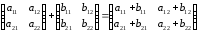 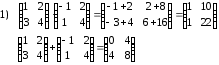 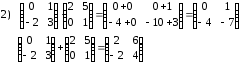 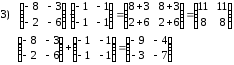 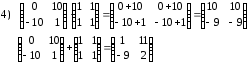 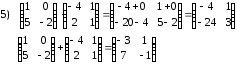 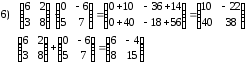 8. Найти определители матриц: 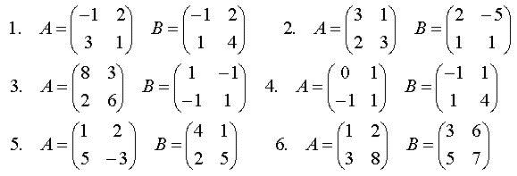 Решение: Определитель матрицы размера 22 находится по формуле: 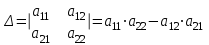 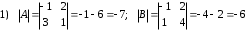 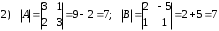 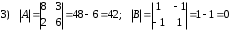 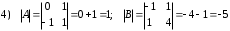 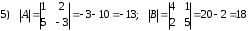 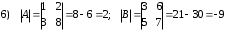 9. Решить систему уравнений: 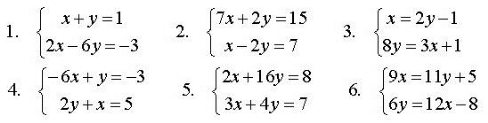 Решение: Запишем систему в виде матричного уравнения АХ = В, где А – матрица размера 22 , а В вектор-столбец размера 21. Тогда (если 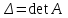 ≠ 0) решение системы находим по формуле: Х = А-1В. Таким образом, находим обратную матрицу к матрице системы и умножаем её на столбец правых частей. ≠ 0) решение системы находим по формуле: Х = А-1В. Таким образом, находим обратную матрицу к матрице системы и умножаем её на столбец правых частей.Для матрицы размером 2 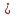 2 обратная матрица находится по формуле: 2 обратная матрица находится по формуле: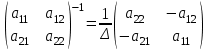 , где определитель матрицы , где определитель матрицы 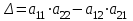 . .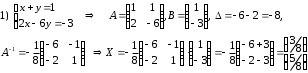 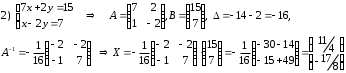 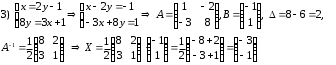 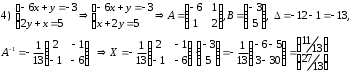 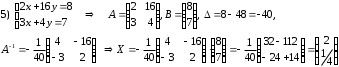 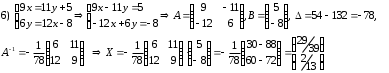 10. Для заданных векторов найти смешанное произведение 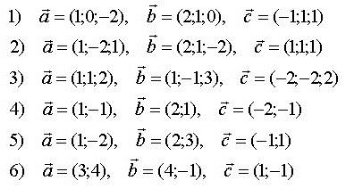 Решение: Смешанное произведение трех векторов размерности 3 равно значению определителя, составленного из координат этих векторов. Определитель 3-го порядка вычисляем разложением по 1-й строке.
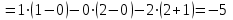 . .
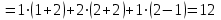 . .
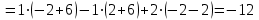 . .Модуль смешанного произведения численно равен объёму параллелепипеда, образованного этими векторами. Для двумерных векторов объем такого параллелепипеда равен нулю, так как двумерные векторы лежат в одной плоскости. Поэтому смешанное произведение 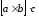 двумерных векторов равно нулю. Таким образом, для пунктов 46 смешанное произведение двумерных векторов равно нулю. Таким образом, для пунктов 46 смешанное произведение 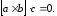 |