ЛиналБилеты. Вопросы к экзамену по линейной алгебре

• Название: Вопросы к экзамену по линейной алгебре
• Анкор: ЛиналБилеты.docx
• Дата: 19.03.2018
• Размер: 155.76 Kb.
• Имя файла: ЛиналБилеты.docx
• Тип: Вопросы к экзамену; #16911
• страница: 1 из 9

Вопросы к экзамену по линейной алгебре

МП-1А

1. 
   Поле. Примеры полей. Поле остатков от деления на p.
   
2. 
   Линейное пространство над полем. Его простейшие свойства.
   
3. 
   Линейно зависимые и независимые системы векторов. Их свойства.
   
4. 
   Полные системы векторов. Их свойства.
   
5. 
   Базис линейного пространства. Единственность разложения по базису.
   
6. 
   Лемма Штейница и следствия из нее. Размерность линейного пространства.
   
7. 
   Подпространство линейного пространства. Сумма и пересечение подпространств.
   
8. 
   Линейная оболочка совокупности векторов.
   
9. 
   Размерность суммы подпространств.
   
10. 
    Подстановки. Количество инверсий. Транспозиции. Обратная подстановка.
    
11. 
    Операции над матрицами. Ассоциативность произведения матриц.
    
12. 
    Определитель. Неизменность определителя при транспонировании матрицы. Линейность определителя.
    
13. 
    Перестановка строк (столбцов) определителя. Определитель с двумя одинаковыми строками (столбцами).
    
14. 
    Определитель блочной матрицы.
    
15. 
    Разложение определителя по строке (столбцу).
    
16. 
    Определитель произведения матриц.
    
17. 
    Элементарные преобразования матриц. Приведение матрицы к ступенчатому виду.
    
18. 
    Ранг матрицы. Теорема о базисном миноре.
    
19. 
    Обратная матрица: единственность, условие существования, методы вычисления.
    
20. 
    Правило Крамера.
    
21. 
    Свойства решений однородной системы линейных уравнений. Связь решений однородной системы с решениями неоднородной.
    
22. 
    Фундаментальная система решений однородной системы.
    
23. 
    Переход к другому базису в линейном пространстве.
    
24. 
    Линейные операторы. Матрица линейного оператора. Связь координат образа и прообраза.
    
25. 
    Изменение матрицы линейного оператора при изменении базиса.
    
26. 
    Собственные векторы и собственные значения линейного оператора. Характеристическое уравнение.
    
27. 
    Свойство собственных векторов линейного оператора.
    
28. 
    Условие приведения матрицы к диагональному виду.
    
29. 
    Евклидовы и унитарные пространства. Неравенство Шварца. Геометрия евклидовых пространств.
    
30. 
    Ортогональный и ортонормированный базис. Процесс ортогонализации Грама-Шмидта.
    
31. 
    Ортогональные матрицы.
    
32. 
    Симметрические (самосопряженные) операторы. Свойства их матриц.
    
33. 
    Свойства собственных значений и собственных векторов симметрического оператора. Существование для симметрического оператора ортонормированного базиса из собственных векторов.
    
34. 
    Линейные, билинейные и квадратичные формы.
    
35. 
    Матрица квадратичной формы. Изменение матрицы при изменении базиса.
    
36. 
    Приведение действительной квадратичной формы к нормальному виду.
    
37. 
    Положительно определенные и отрицательно определенные квадратичные формы. Критерий Сильвестра.
    

БИЛЕТ 1. Поле. Примеры полей. Поле остатков от деления на p.

Определение поля: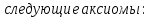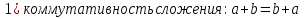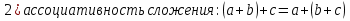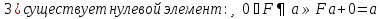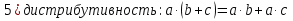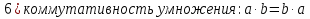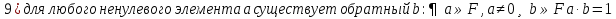

Элементы поля принято называть скалярами.

Примеры полей: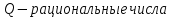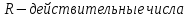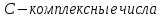

Множество 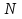натуральных чисел полем не является, так как в нем не выполняется 9 аксиома.

Свойства поля:

Доказательство: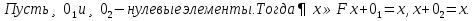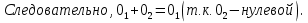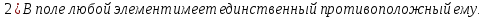











Доказательство: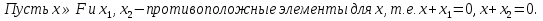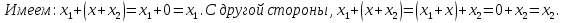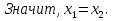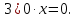









Доказательство: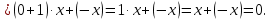







Доказательство: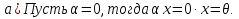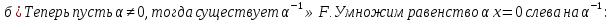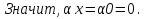









.