Финансы и романсы. Решение Формула для схемы пренумерандо выглядит следующим образом Где s накопленная сумма, руб
 Скачать 24.57 Kb. Скачать 24.57 Kb.
|
|
Задача 11. Вы намерены сделать подарок в сумме 10 000 долл. своему 13-летнему сыну на момент его совершеннолетия (18 лет). С этой целью вы намерены заключить договор с банком, согласно которому вы будете делать ежеквартальные взносы в банк (схема пренумерандо), на которые банк ежегодно будет начислять проценты по ставке 8% годовых. Определите величину взноса. Какую сумму нужно было бы единовременно положить в банк сегодня, чтобы достичь той же цели? Решение : Формула для схемы пренумерандо выглядит следующим образом: 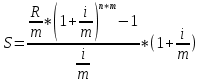 Где S – накопленная сумма, руб., R/m – взносы, осуществляемые в начале каждого периода, руб., i – сложная годовая процентная ставка, доли единицы, n – количество лет, в течении которых вносятся платежи. При этом i/m = 0,08/4 (так как выплаты квартальные), n*m = 5*4 = 20 (так как 5 лет по 4 квартала). Из этого уравнения выражаем R/m – ежеквартальные взносы: 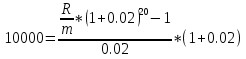 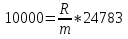 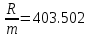 долларов. долларов.Определим размер единовременного взноса по формуле: 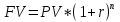 Тогда 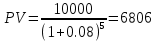 Единовременно нужно положить 6806 долларов. Задача 12. Какой срок необходим для того, чтобы на депозите накопилось 20 млн руб., при условии, что на ежегодные взносы в сумме 2 млн руб. начисляются сложные проценты по ставке 7% годовых? Взносы на депозит делаются в начале каждого года. Как изменится срок, если взносы на депозит будут в конце каждого года? Из формулы 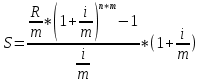 выражаем n: выражаем n: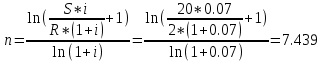 Если взносы на депозит будут в конце каждого периода, то 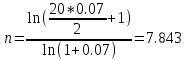 Задача 20. Вы имеете на счете 40000 долл. и прогнозируете свой доход в течение следующих 2 лет в сумме 60000 долл. и 70000 долл. (схема пренумерандо), соответственно. Ожидаемая процентная ставка в эти годы будет 8 и 14 %. Ваши минимальные расходы составят в текущем году - 20000 долл., в следующие годы ожидается их прирост с темпом 10% в год (схема постнумерандо). Рассчитайте потенциально доступную к потреблению сумму в каждом из следующих 2 лет. Пренумерандо - поступления происходят в начале периода. Постнумерандо - поступления происходят в конце периода. 1. Считаем доходы от тех денег, что уже лежат на счете: PV = 40000; процентная ставка в 1-й год = 8% и во 2-й год = 14%; FV = ? FV = PV*(1+i)^n FV1года = 40000*(1+0,08)^1 = 43200 FV2 года = 43200*(1+0,14)^1 = 49248 2. Считаем доходы от будущих поступлений по схеме пренумерандо PMT1года = 60000; PMT2года = 70000; i в 1-й год = 8% и во 2-й год = 14%; FV1года = 60000*0,926=55560 долл. FV2года = 70000*0,877 = 61390 долл. 3. Далее складываем доходы по каждому году отдельно, вычитаем расходы и получается потенциально доступную сумму к потреблению: Расходы 1 года = 20000 долл., расходы 2 года = 22000 долл. 43200+55560-20000=78760 долл. Доступно к потреблению в первом году. 49248+61390-22000 =88638долл. Доступно во втором году к потреблению. Задача 19. Вы заняли на 4 года 10 000 тыс. долл. под 14% , начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Определите величину годового платежа Имеется постоянный аннуитет постнумерандо с периодом один год и равным ему периодом начисления процентов. Базовая формула 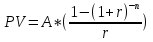 , где , где PV – исходная (приведенная) стоимость аннуитета (10 000 долл.); А – исходная (приведенная) стоимость (искомое); n – число периодов начисления процентов (4 года); r – процентная ставка (14%). Для решения задачи преобразуем исходную формулу: 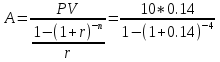 = 3.432 = 3.432Годовой платеж составляет 3432 долл. Задача 18. Работник заключает с фирмой пенсионный контракт на 20 лет, согласно которому на счет работника в банке в конце каждого двухлетнего периода будет поступать по 150 тыс. руб. Требуется определить наращенную сумму к концу действия контракта, если на поступающие платежи ежегодно будут начисляться сложные ссудные проценты по ставке 8% годовых. В соответствии с контрактом денежные суммы образуют аннуитет длительностью 20 лет и с периодом 2 года. Таким образом, период аннуитета больше базового периода начисления процентов, равного году. Полагая A = 150, n = 20, n =2, r = 8%, по формуле оценки постоянного аннуитета постнумерандо, период которого больше базового периода начисления процентов получим: FVpst = 150 ⋅ FM3(8%, 20)/ FM3(8%, 2) = 150 * 45,762 /2,080 = 3300,14 тыс. руб. Задача 17. Стоит ли покупать за 55 000 руб. ценную бумагу, генерирующую ежегодный доход в сумме 60 000 руб. в течение 50 лет? При расчетах использовать сложную ставку 10% годовых, начисляемую ежеквартально. Доход, получаемый в течение 50 лет, представляет собой аннуитет постнумерандо с A = 60000, n = 50, r = 40%( годовых). Для ответа на вопрос, стоит ли приобретать ценную бумагу за 55000 руб., необходимо найти приведенную стоимость данного аннуитета и сравнить ее с величиной 55000. Используя финансовые таблицы, получаем: PVpst = 60000 ⋅ FM4(40%, 50) = 150000 руб. Таким образом, ценную бумагу стоит приобретать. Задача 16. В течение 5 лет на счет в банке ежедневно будут поступать одинаковые платежи, каждый год составляя в сумме 300 тыс. руб. Определите сумму, накопленную на счете к концу пятилетнего срока при использовании сложной процентной ставки 8% годовых, считая, что платежи поступают непрерывным образом. Для определения наращенной суммы непрерывного аннуитета при А = 300, n=5, m = 1, r = 0,08. 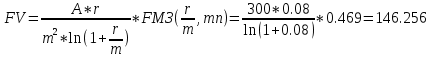 К концу пятого года на счете в банке накопится 146 256 000 руб. Задача 15. За 10 лет предпринимателю необходимо накопить 50 млн руб.. Для этого предприниматель планирует ежегодно вносить некоторую сумму в банк, ежегодно начисляющий сложные проценты по ставке 10% годовых. Какой величины должен быть первый вклад, если предполагается каждый год увеличивать платежи на 400 тыс. руб.? Денежные поступления осуществляются в начале каждого года. FVpst=50000 тыс.руб. z= 400 тыс. руб. n= 10 r= 0,1 Будущая стоимость аннуитета пренумерандо, платежи которого образуют арифметическую прогрессию: FVpre = (1 + r) ⋅ (A + z/r )*FM3 (r, n) − (1 + r)* zn/r . Отсюда выражаем А и получаем: 50000=1,1*(А+(400/0,1)*FM3(10,10)-(400*10/0,1)*(1,1), тогда A = 1362 тыс. руб - размер первого вклада. |
